Hello everyone.
I would like to invite you to participate in the 8th COJ (Caribbean Online Judge) Round, this will be a contest with 5 problems, and three hours of duration. The problems will have Div2-like complexity and will be in English and Spanish. The contest will have ACM-ICPC format.
You can find out more about it clicking here. You can also check out the previous rounds here.
UPD1: Time of the contest has changed because of overlapping with Euro Semifinals :). The contest will start at this time.
UPD2: The contest is about to start, get in now!!.
UPD3: The contest is over. Hope you liked the problems.
Hints:
Problem A:
The last player to play wins. Note that this last player can always get what the previous player got in the previous turn plus another positive number. Watch out with n = 1 case.
Complexity: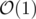 
Problem B:
You can start from the right: i = n, decreasing k with i - 1 while k ≥ i - 1 and append to a vector the number i. Then you can append the rest of the numbers (in increasing order) to the vector.
Complexity: 
Problem C:
Note that the graph is a tree with a cycle. The probability to disconnect the graph in one step is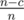 
and in two steps is 
. So the expected value is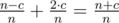 
. Here c is the length of the cycle. You can do a dfs to find c.
Complexity:
Problem D:
A number is hyperdrome if it have at most 1 digit with odd frequence. So build a graph where each node is a bitmask representing the parity of the digits's frequence of a number. Add edges between node x and nodes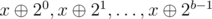 
.
Also add a node that represents the empty set, and add and edge to itself, and to 21, 22, ..., 2b - 1.
Then you can exponentiate this graph to obtain the answer.
Complexity: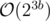 
Problem E:
Segment Tree. In each node save the lcp of the range, and a string that is in the range. Then to combine two nodes you can do:
lcp[x] = min (lcp[2 * x], lcp[2 * x + 1], GetLCP(str[2 * x], str[2 * x + 1]))
str[x] = str[2 * x]
Where x is a node in the segment tree and GetLCP is a function that calculates the LCP for two strings. Also you should add lazy propagation to this.
Complexity: 
