710A - Ходы короля
Легко видеть, что в задаче возможно всего три случая. Если король находится углу доски, то у него 3 возможных хода. Если он стоит на краю доски, то у него 5 возможных хода (если конечно он не в углу). Наконец, если король не стоит на краю доски, то у него всего 8 возожных хода.
Сложность: O(1).
710B - Оптимальная точка на прямой
Легко видеть, что ответ всегд находится в одной из заданных точек (функция суммарного рассояния между парой заданных точек монотонна). Далее можно либо для каждой точки посчитать суммарное расстояние и выбрать оптимальную точку, либо заметить, что ответом является точка находящяяся посередине в отсортированном списке заданных точек (если точек чётное количетсво то слева посередине). Последний факт легко доказыватся, но можно это и не делать и сдать задачу первым способом.
Сложность: O(nlogn).
710C - Магический нечётный квадрат
Задачу предложил Resul Hangeldiyev Resul.
Решение задачи легко получить из второго примера. Легко видеть, что если расставить все нечётные числа в виде ромба посередине квадрата, то мы получим магический квадрат.
Сложность: O(n2).
710D - Две арифметические прогрессии
Эту задачу я уже давно хотел дать на раунд, она мне казалась очень стандартной, но я недооценил её сложность.
Запишем уравнение, которое описывает все решения задачи: a1k + b1 = a2l + b2 → a1k - a2l = b2 - b1. Имеем линейное диофантово уравнение с двумя неизвестными: Ax + By = C, A = a1, B = - a2, C = b2 - b1. Его решение имеет вид: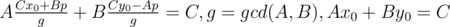 
, где последнее уравнение решается с помощью расширенного алгоритма Евклида, а p произвольное целое число. Далее нам нужно удовлетворить двум условиям: 
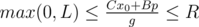и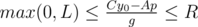 
. Поскольку мы знаем знаки чисел A и B, последние уравнения задают отрезок возможных значений для переменной p, длина этого отрезка и является ответом на задачу.
Сложность: O(log(max(a1, a2))).
