Hello everyone,
finding the diameter is one of the most frequent ways to solve problems about trees. In this tutorial we will see how to find a diameter and some of its properties, and we will use them to solve some problems of increasing difficulty.
The first part of the tutorial is quite basic, so feel free to skip it and jump to the problems if you already know the concepts.
Target: rating $$$[1400, 2300]$$$ on CF
Prerequisites: basic graph theory, greedy
The diameter
Given an unweighted tree, let's define $$$\text{dist}(a, b) =$$$ the number of edges in the simple path $$$a \rightarrow b$$$.
A diameter of the tree $$$a \rightarrow b$$$ is the longest path, i.e., the one that maximizes $$$\text{dist}(a, b)$$$ over all pairs of nodes. If there are multiple diameters, let's pick any of them.
The same definition is valid for a weighted tree with nonnegative weights (with $$$\text{dist}(a, b) =$$$ the sum of the weights of the edges in the simple path $$$a \rightarrow b$$$).
Finding a diameter
Given a tree with $$$n$$$ nodes are multiple ways to find a diameter. Here is one of the simplest ways:
Run a DFS from any node $$$p$$$. Let $$$a$$$ be a node whose distance from node $$$p$$$ is maximized. Run another DFS from node $$$a$$$. Let $$$b$$$ be a node whose distance from node $$$a$$$ is maximized. $$$a \rightarrow b$$$ is a diameter.
Tree = edges of a diameter + forest
Before proving the previous algorithm, let's analyze the structure of the tree (we will mention the diameter, but we will not use the fact that $$$a \rightarrow b$$$ is actually a diameter before proving it).
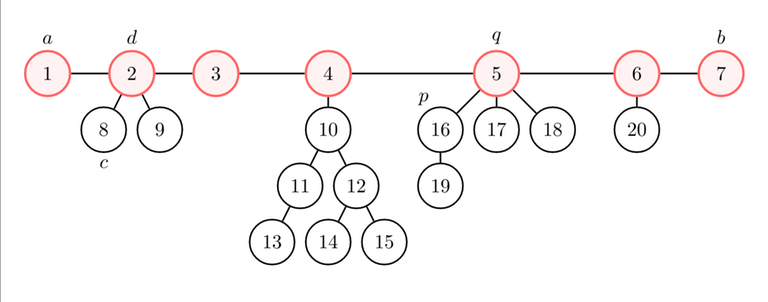
We started a DFS from node $$$p = 16$$$, and we got that node $$$a = 1$$$ is the farthest from $$$p$$$, and node $$$b = 7$$$ is the farthest from $$$a$$$.
Let's represent the diameter on a line. If you remove the edges of the diameter, you get a forest (i.e., several trees). Let's root each tree at the node in the diameter. What's the height (i.e., the maximum distance from the root to any node) of each component?
Let $$$q$$$ be the root of the component of $$$p$$$. Let's consider any component whose root $$$d$$$ is between $$$a$$$ (included) and $$$q$$$ (excluded), and one of its nodes $$$c$$$.
We get
$$$\text{dist}(p, a) \geq \text{dist}(p, c) \implies \text{dist}(p, a) - \text{dist}(p, d) \geq \text{dist}(p, c) - \text{dist}(p, d) \implies \text{dist}(a, d) \geq \text{dist}(c, d)$$$.
In other words, the height of each component with root in the left half of the diameter (i.e., $$$\text{dist}(a, d) < \text{dist}(d, b)$$$) is at most the distance of the root of the component from the left end of the diameter.
You can prove the same statement for the right half of the diameter (i.e., $$$\text{dist}(a, d) \geq \text{dist}(d, b)$$$), using that $$$b$$$ is the farthest node from $$$a$$$.
Farthest node for each node
For each node $$$i$$$, let's find a node $$$j$$$ such that $$$\text{dist}(i, j)$$$ is maximum.
Claim: $$$j = a$$$ or $$$j = b$$$ always works.
Proof:
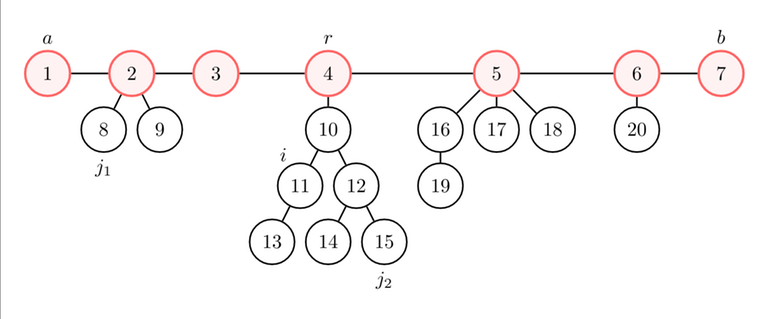
- If $$$j = j_1$$$ works ($$$j_1$$$ is not in the same component of $$$i$$$; let's assume without loss of generality that $$$j_1$$$ is closer to $$$a$$$ than to $$$b$$$), $$$\text{dist}(i, j_1) = \text{dist}(i, r) + \text{dist}(r, j_1) \leq \text{dist}(i, r) + \text{dist}(r, a) = \text{dist}(i, a)$$$. Then, $$$j = a$$$ also works.
- If $$$j = j_2$$$ works ($$$j_2$$$ is in the same component of $$$i$$$), $$$\text{dist}(i, j_2) \leq \text{dist}(i, r) + \text{dist}(r, j_2) \leq \text{dist}(i, r) + \text{dist}(r, a) = \text{dist}(i, a)$$$. Then, $$$j = a$$$ also works.
Proof that $$$a \rightarrow b$$$ is a diameter
Now we can finish the proof.
Suppose that $$$u \rightarrow v$$$ is a diameter. We have either $$$\text{dist}(u, a) \geq \text{dist}(u, v)$$$ or $$$\text{dist}(u, b) \geq \text{dist}(u, v)$$$ (see "Farthest node for each node").
Let's assume without loss of generality that $$$\text{dist}(u, b) \geq \text{dist}(u, v)$$$. We get $$$\text{dist}(a, b) \geq \text{dist}(u, b) \geq \text{dist}(u, v)$$$, so $$$a \rightarrow b$$$ is a diameter.
Observations
The algorithm also works in a weighted tree with positive edges (we've never used that the weights are $$$1$$$).
However, it doesn't work on general graphs (discussion).
How to use the diameter
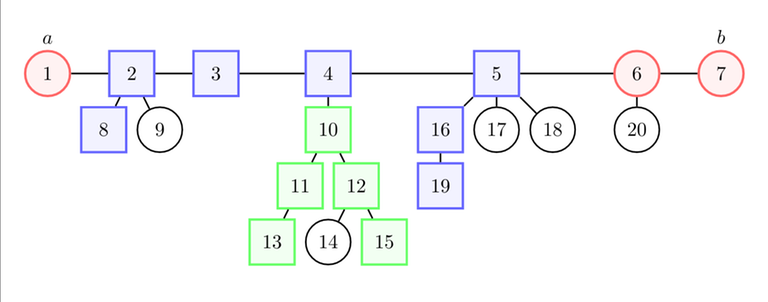
Most of the times, spamming "the farthest node from each node is one end of the diameter" and "the height of each component is smaller than the distance to the closest end of the diameter" is enough to reduce the problem to something simpler.
Find a diameter $$$a \rightarrow b$$$ (from now, $$$a \rightarrow b$$$ will always be a diameter, unless otherwise stated). Now, you may need to consider any path of the tree. There are two cases: the path intersects (blue) or doesn't intersect (green) the diameter.
Then, you may wonder how to make the path longer / "more optimal" / etc. according to the statement. For example, you may need to use $$$\text{dist}(7, 5) \geq \text{dist}(5, 19)$$$ to show that $$$8 \rightarrow 7$$$ is "more optimal" than $$$8 \rightarrow 19$$$.
1004E - Sonya and Ice Cream (rating: 2400)
Implementation by nor (C++): 151009669
633F - The Chocolate Spree (rating: 2600)
Implementation by nor (C++): 151018941
1434D - Roads and Ramen (rating: 2800)
Implementation by nor (C++): 151024814
Other problems
CSES — Tree Distances I (to check your implementation) (suggested by nor)
102694B - Dynamic Diameter
1404B - Tree Tag (flashmt)
734E - Anton and Tree (preet_25)
456E - Civilization (TiredRetiredThread)
Code Jam 2022 — Interesting Outing (srishtik_16)
abc221_f
IOI 2013 — Dreaming (timreizin)
agc033_c (antontrygubO_o)
arc117_d (flashmt)
USACO 2018 — New Barns (Olympia)
1617E - Christmas Chocolates (feecIe6418)
arc108_f (feecIe6418)
IOI 2015 — Towns (defnotmee)
1214H - Tiles Placement (lrvideckis)
CEOI 2019 — Dynamic Diameter (hard) (nor)
RMI 2021 — Paths (hard) (ntherner)
Conclusions
We've seen that finding a diameter can also solve seemingly unrelated problems, and it's a good candidate idea if the problem involves a tree and maximum lengths/distances.
Of course, suggestions/corrections are welcome. In particular, please share in the comments other problems where you have to use the diameter.
I hope you enjoyed the blog!











Nice blog! CSES has a problem that requires the "farthest node for each node" trick (Tree Distances I). If I recall correctly, there was a certain recent CEOI problem with a nice trick related to diameters too.
a somewhat related USACO plat problem
AGC033C
https://oj.uz/problem/view/IOI15_towns
Diameter finding to its fullest
Another Diameter of Tree Problem: Problem
Some slightly easier problems:
another problem: ARC108F
One very surprising problem that seems unrelated, but actually uses diameter: 1617E - Christmas Chocolates
One more Problem :- E. Anton and Tree
This is a good problem too
Another useful thing about diameters is "merging diameters":
Problem: Consider some tree, at the beginning all nodes are unmarked. You should handle queries of type: mark some unmarked node and print out 2 most distant nodes that are marked.
It is enough to keep the 2 most distant nodes $$$a$$$ and $$$b$$$, after adding node $$$i$$$ you need only to consider these possibilities as new diameter: $$$(a, b)$$$, $$$(a, i)$$$, $$$(b, i)$$$. Distance queries can be solved in $$$O(\log{n})$$$ using LCA. After each query print out the ends of diameter.
Complexity: $$$O(n\log{n})$$$
Problem 2: Handle queries of type: answer with 2 most distant nodes that are inside segment $$$[l,r)$$$ of array $$$a$$$, where $$$a$$$ is some permutation of nodes from $$$1$$$ to $$$n$$$
Use segment tree.
At each node of segment tree store the merged diameter of nodes contained in that segment (only 2 most distant nodes $$$a$$$ and $$$b$$$), merging two ranges $$$[l, r)$$$ and $$$[l2, r2)$$$ can be done in $$$O(\log{n})$$$ (as explained in above problem, consider each pair of $$$a$$$ $$$b$$$ $$$c$$$ $$$d$$$ where $$$a$$$ and $$$b$$$ are most distant nodes in left node and $$$c$$$ and $$$d$$$ are most distant nodes in right node) and there is also $$$O(\log{n})$$$ ranges when querying the segment tree.
Complexity: $$$O(q\log^2{n})$$$.
I found this problem from one "Centroid Decomposition" blog , but then I remembered this comment :)
It's almost the same as USACO 2018 — New Barns (already in the blog).
Can you prove the solution of problem 1, i don't understand why we only need (a,i),(b,i),(a,b) to find a new diameter.
Hope I don't trigger some PTSD, but a friend told me some such tricks as you have mentioned could lead to a correct solution to this problem
You don't trigger any PTSD, I'm already used to fail contests.
https://codeforces.net/contest/1214/problem/H
Hey all, this is a question about finding the longest possible diameter of a tree given that you can remove one edge, and replace that edge somewhere else ONLY ONCE. https://codebreaker.xyz/problem/treecutting
It seems like i can use the "multiple trees/forests on the diameter" idea to solve this, i.e., find the diameter, and find the largest diameter among all the components, and add them up. However my question is that what if there are multiple diameters in a tree — How will constructing my forests based on different diameters affect the diameters of the components produced?
Any other ideas on how to solve this problem is greatly appreciated. Thank you!
more good tasks
1) 1805D - A Wide, Wide Graph
2) 1146C - Tree Diameter
3) Jeanies Route
thanks, great article
How we get dist(p,a) >= dist(p,c) in general ?
How we get dist(p,a) >= dist(p,c) in general ?
Here is a nice result about diameters of trees. I haven't seen it in any cp problems but it seems like it could be applied somewhere. I'm not sure how to find such a vertex efficiently though, so that may be a nice problem.
For any tree, there exists some vertex such that all diameters (longest paths) of the tree contain that vertex.
If the diameter has length $$$k$$$, its $$$\lceil k/2 \rceil$$$-th node has this property.
Sketch of proof: if you remove that node from the tree, you can find a bound on the length of the remaining paths.
Yep, using this you can find the nodes of all of the diameters of a tree if there are multiple. First, find one diameter using DFS. Then, find the center of the diameter (there may be 2 if the diameter is of an even length) . Finally, run a BFS to find all of the diameters in $$$O(n)$$$ time (run BFS on both center nodes if there are 2).
This is a problem in which it's helpful to think about the tree as the diameter and some disjoint trees hanging from nodes on the diameter. In fact it allows us to arrive at a more efficient solution than the official editorial's solution (wrote a comment in the editorial blog).
This is also a good problem on similar idea (rating: 1700) https://codeforces.net/contest/1881/problem/F
Thanks for great explanation, one more problem to practice: 14D - Two Paths (and my solution)
.
Nice blog! I have a question: Is it possible to answer online tree diameter queries, with the update being to change an edge's length, having O(Q*logn)?
Nvm it was not consistent.
ignore it.
Add a problem: 1458F, which is one of the hardest problems using this theory.
Another good problem