Codeforces Round #370 Editorial

Revision en5, by send_nodes, 2016-09-11 19:42:28

Hi everyone, here are the solutions to the contest problems.

712A — Memory and Crow

Note that b[i] + b[i + 1] = a[i]. Use the initial condition b[n] = a[n] and we can figure out the entire array a.

Time Complexity: O(n)

Code

712B — Memory and Trident

First, if S has odd length, there is no possible string because letters must come in opposite pairs. Now, let's denote the ending coordinate after following S as (x, y). Since S has even length, |x| has the same parity as |y|. Suppose they are both even. Then clearly, we can make x = 0 in exactly 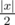moves, and same for y. If instead they are both odd, then we can change exactly one x-character into a y-character. With the correct choices of these characters, now our string has |x| and |y| with even parity, thus reducing to the problem above. Therefore, the answer is (|x| + |y|) / 2.

Time Complexity: O(|S|)

Code

712C — Memory and De-Evolution

Let's reverse the process: start with an equilateral triangle with side length y, and lets get to an equilateral triangle with side length x. In each step, we can act greedily while obeying the triangle inequality. This will give us our desired answer.

Time Complexity: O(log x)

Code

712D — Memory and Scores

One approach to this problem is by first implementing naive DP in O((kt)2). The state for this is (diff, turn), and transitions for (diff, turn) is the sum (diff - 2k, turn - 1) + 2(diff - 2k + 1, turn - 1) + 3(diff - 2k + 2, turn - 1) + ... + (2k + 1)(diff, turn - 1) + 2k(diff + 1, turn - 1) + ...  + diff( + 2k, turn - 1).

Now, if we use prefix sums of all differences in (turn-1), along with a sliding window technique across the differences, we can cut a factor of k, to achieve desired complexity O(kt2).

However, there is a much nicer solution in O(kt log kt) using generating functions(thanks to minimario). We can compute the coefficients of 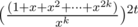, and the coefficient to xi corresponds to the number of ways we can form the difference i. To compute these coefficients, we can use the binomial theorem.

Time Complexity: O(kt2)

Code

Time Complexity: O(kt log kt)

Code

712E — Memory and Casinos

Lets think about two segments of casinos [i, j] and [j + 1, n]. Let L([a, b]) denote the probability we dominate on [a, b], and let R([a, b]) denote the probability we start on b and end by moving right of b. Let

l1 = L([i, j]),

l2 = L([j + 1, n]),

r1 = R([i, j]),

r2 = R([j + 1, n]).

You can use a geometric series to figure out both L([i, n]) and R([i, n]) using only l1,l2,r1, and r2. To derive these series, think about the probability we cross over from j to j + 1 once, twice, three times, and so on. The actual formulas are,

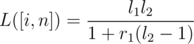
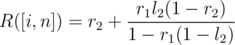
Now we can build a segment tree on the casinos, and use the above to merge segments.

Time Complexity: O(N + QlogN)

Code

History

 
 
 
 
Revisions
 
 
  Rev. Lang. By When Δ Comment
en7 English send_nodes 2016-09-12 20:09:38 2 Tiny change: 're array $a$.\n\nTime' -> 're array $b$.\n\nTime'
en6 English send_nodes 2016-09-12 20:08:52 6 Tiny change: 'ote that $b[i]+b[i+1] = a[i]$. Use ' -> 'ote that $a[i]+a[i+1] = b[i]$. Use '
en5 English send_nodes 2016-09-11 19:42:28 1 Tiny change: '016-09-11]. We can c' -> '016-09-11]). We can c'
en4 English send_nodes 2016-09-11 19:42:00 38 Tiny change: ' functions. We can c' -> ' functions(thanks to [user:minimario]. We can c'
en3 English send_nodes 2016-09-11 00:34:55 2 (published)
en2 English send_nodes 2016-09-11 00:30:40 11305 (saved to drafts)
en1 English send_nodes 2016-09-10 23:31:27 178 Initial revision (published)