Okay so firstly, in hindsight I now see the drawbacks there were in my explanation of the roots of unity and how the divide and conquer works in FFT. So in this blog I would be aiming to give you an intuition of what really FFT exploits over the trivial classical DFT. Also I would be covering up NTT.

Firstly, I am assuming that you have been through the Part 1 (URL).

Okay so the intution for FFT, the part where most of the people find FFT weird or magical is where we convert the polynomial from coefficient form to point value form in N * logN instead of the trivial N². Okay so here is the broad idea

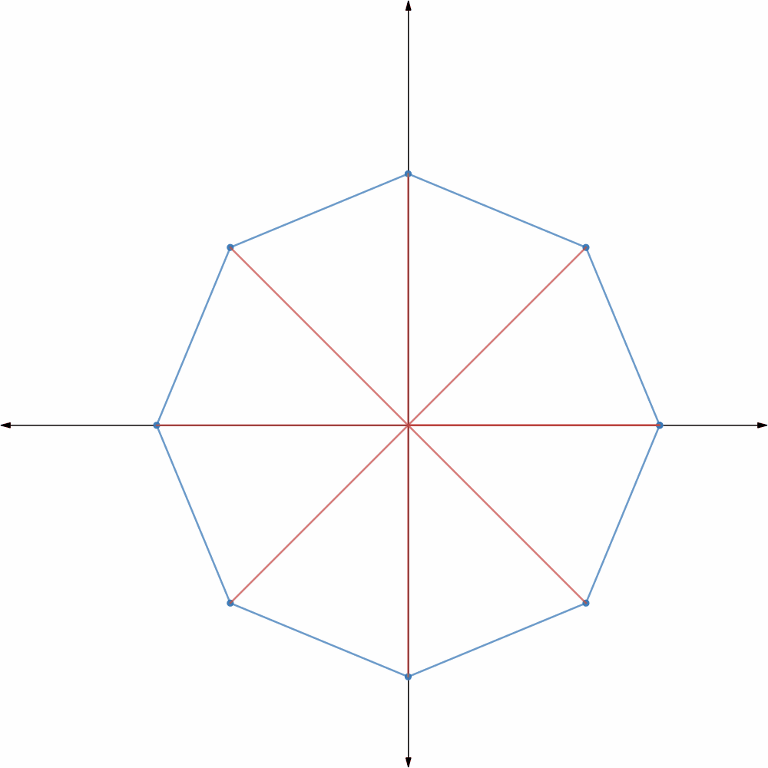
In the notation below I have referred to n complex n^th roots of unity as powers of w_n¹ = e^{2π * i / n}

Assume that you have a 8 terms (7 degree) polynomial you need to convert from coefficient form to point value form. So firstly you choose the powers of the 8^th complex root of unity as the x_i's that you will be plugging in the polynomial. Initially this might seem random but hopefully by the end of this topic it would be clear to you. Okay so now we can reduce our polynomial A(x) as A_even(x²) + x * A_odd(x²) where A_even() is a 4 terms (3 degree) polynomial and A_odd() is also a 4 terms (3 degree) polynomial. Now solving the original problem of converting A(x) from coefficient form to point value form for each of the power of the 8^th root of unity is exactly equivalent to solving this new problem of converting A_even(x²) and A_odd(x²) for powers the 8^th root of unity. So really this doesn't help us much BUT THE TRICK is that when we square (because x²) these powers of the 8^th root of unity, they come out to be same pairwise, ie. the 0^th and 4^th powers of the 8^th root of unity when squared give the same result, similarly, the 1^st and 5^th powers of 8^th root of unity when squared give the same result and so on. Also note that these results actually turn out to be the powers of the 4^th root of unity. Okay, So I gave the dry mathematical proof for this in the previous part, but that time I did not have a visual understanding of it. Well now I do so refer to the animations and diagrams below to get the idea but first read through the below subtopic of Rotation in Imaginary Plane.

Rotation in Imaginary Plane — Okay so as a rule of thumb remember that if you have a complex number lets say Z and you multiply it with e^iθ then it basically rotates it by θ angle in counter — clockwise direction with respect to the origin. So lets say you have 3^rd power of 8^th root of unity, ie. w_n³ = e^{i * 2π * 3 / 8} and you wish to exponentiate it. Then currently the θ is . So if you square it you are actually multiplying the θ by 2 so you are basically rotating it by theta degree in counter — clockwise direction with respect to the origin. Formally raising it by x is (w_n³)^x = e^{i * 2π * 3 / 8 * x} = e^{i * 2π * 3 / 8} * e^{i * 2π * 3 / 8 * (x - 1)} =  rotating e^{i*2\pi*3/8) by (x — 1) * \theta \deg in counter clockwise direction with respect to x axis.

Diagram here.

So given this understanding we can now easily exponentiate roots of unity. So here is the key, when you mark the 8th roots of unity on a graph it is regular octagon whose vertices are making angle 0, 45, 90, 135, 180, 225, 270, 315 degree with respect to positive x axis. Now when you square each of these, the angles double as shown above, so they become 0*2, 45*2, 90*2, 135 * 2, 180 * 2, 225 * 2, 270 * 2, 315 * 2 = 0, 90, 180, 270, 360, 450, 540, 630 = 0, 90, 180, 270, 0, 90, 180, 270 which are basically the points of the 4th root of unity. Below is a beautiful animation showing the same.

Here you can clearly grasp the complexity of T(n) = T(n / 2) (For A_even()) + T(n / 2) (For A_odd()) + O(2 * n)(For combining the results as A_even(x²) + x * A_odd(x²))

NTT (Number Theoretic Transform) — The objective of NTT is to multiply 2 polynomials such that the coefficient of the resultant polynomials are calculated under a particular modulo. The benefit of NTT is that there are no precision errors as all the calculations are done in integers. A major drawback of NTT is that generally we are only able to do NTT with a prime modulo of the form 2^k * c + 1, where k and c are arbitrary constants. So for doing it for a random mod we would need to use CRT (Chinese Remainder Theorem).

Firstly, nth roots of unity under a primitve field, ie.  ± od P are defined as zⁿ = 1 ± od P, where P is only considered as prime for simplicity.

Okay so using Fermat's Little Theorem we know that 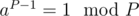, where gcd(a, P) = 1, which will be true always when P is prime and a < P.

Here we are assuming that our prime mod P = 2^k * c + 1, where c, k are positive integers.

Note — All the calculation done below are done under modulo P including the operations in the power ex. r^P + 5 = r⁵. I have skipped the modulo sometimes as it makes the notation way too ugly.

So we first find a r such that 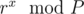goes through all the numbers from 1 to P - 1 when x goes from 1 to P - 1. Note that 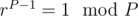is already a fact. After finding one such r, our (2^k)^th root of unity under the modulo field of P will be r^c. The powers will be as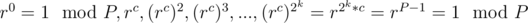

Lemma 1 — Here (r^c)^x, 1 ≤ x < 2^k is not equal to because 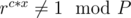when x < 2^k, this is because r is itself defined as the (P - 1)^th root of unity, ie. any power of r less than P - 1 will not be equal to , and as P - 1 = 2^k * c, therefore any power of r where c is multiplied by anything less than 2^k wont give .

So, r^c is now the (2^k)^th root of unity under the modulo field of P. Now the only difference between NTT and FFT will be that the N^th root of unity changes from w to r^c, where r is found by hit and trial method.

Lemma 2 — Another key observation here is that no two (r^c)^α = (r^c)^βwhere\alpha \neq \beta$ and both lie between [1, 2^k]. This observation can be proven by contradiction, assuming that r^c * α = r^c * β under 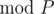then 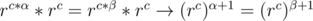, and which can be generalised to (r^c)^α + γ = (r^c)^{\beta + \gamma}where\gamma$ is an integer, but we know for a fact that 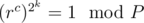, so lets put γ such that α + γ = 2^k, so now 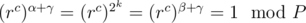. Meaning that if (r^c)^α = (r^c)^β then 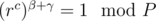where β + γ ≠ 2^k}. This is contradictory to the result mentioned in Lemma 1, hence proved.