Suppose we want to solve a problem by doing binary search on answer. Then the answer will be checked against jury's answer by absolute or relative error (one of them should be smaller then eps). For simplicity we will assume that our answer is always greater than 1 and smaller than B. Because of that, we will always use relative error rather than absolute.

Suppose we have made n iterations of our binary search~--- what information do we have now? I state that we know that real answer is lying in some segment [x_i, x_i + 1], where 1 = x₀ < x₁ < ... < x_i < ... < x_2ⁿ = B. And what is great~--- we can choose all x_i except for x₀ and x_2ⁿ.

Now, for simplicity, we will also assume that we will answer x_i + 1 for segment [x_i, x_i + 1] and the real answer was x_i~--- it is the worst case for us. It is obvious that we will not do that in real life, any other answer would be better, but you will get the idea.

So, what is our relative error? It is 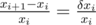. Worst case for us is when relative error is maximal. It is logical to make them equal~--- exactly what we do by binary search with absolute errors. 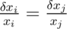. We can assume that δ x_i«x_i so 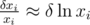. Now we have 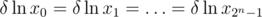, but , so 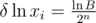. How large should be n to get error less than eps? 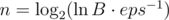. Much smaller than .

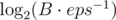How to write such binary search? We want to choose mid in such a way that 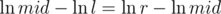or simply .

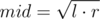Now I want to deal with some assumptions I made.

How to choose answer in the end? Again, 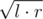(it is the same as dividing the segment in binary search).

What to do if the answer can be smaller than 1? Try 1; if answer is smaller than 1~--- use standard binary search (because absolute error smaller than relative); is answer is bigger than 1~--- use the binary search above.

P.S. I have never heard about this idea and come up with this while solving 744D - Hongcow Draws a Circle. I'm sorry if it is wide known for everyone except for me.