PA

This is a relatively simple problem. We only need to check if the sum of the lengths is larger than m times 60.

簡單題。判斷所有的歌曲長度加起來有沒有大於 m 的 60 倍。

PB

This problem is asking the index of the very next Fibonacci number. The takeaway point is that there is only a small amount of Fibonacci numbers in the range of 32-bits integer. Also, overflow needs to be considered if you choose to use 32-bits integer instead of 64-bits data types.

這題是在問下一個費波那契數列中數字是第幾個。一個小重點是 32 位元整數範圍內的費波那契數列很稀少。另外如果使用 32 位元非 64 位元資料型態的話，那必須考慮溢位的問題。

PC

https://en.wikipedia.org/wiki/Great-circle_distance

https://zh.wikipedia.org/wiki/大圓距離

PD

We binary search the answer. To check if time T is sufficient, we check the maximum flow of the following new constructed graph:

Firstly, we split every vertex v in the original graph into 2 × t vertices in the new graph (v, dir, t) where 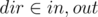and t is the time index starting from 1. Then, we construct the following capacity 1 directional edges:

• (v, in, t) → (v, out, t) for all v and 1 ≤ t ≤ T.
• source to all (v, in, 1) for all v which has an airplane initially.
• (v, out, t) to sink for all v which is a runway and all 1 ≤ t ≤ T.
• (v_i, out, t - 1) → (v_j, in, t) and (v_j, out, t - 1) → (v_i, in, t) for all 2 ≤ t ≤ T and all (v_i, v_j) pairs having an edge in the original graph.

The time complexity of each flow using dinic is O(TE) where E is the number of edges since we have at most T units of flow. We have O(E) = O(nm) and O(T) = O(n), along with the complexity of binary search the overall complexity is .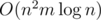

我們可以用二分搜尋來找答案。對於每個可能的答案 $T$，我們可以用以下的方法建立一個新的圖並檢查它的最大流：

首先，對於每個原始圖裡面的點 v，我們在新圖裡建立 2 × t 個點 (v, dir, t)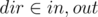， 以及 t 代表從 1 開始的時間點。 接下來，我們用以下的方法建邊：

• 對於所有的 v 以及 1 ≤ t ≤ T 建立 (v, in, t) → (v, out, t) 的邊。
• 對於所有一開始有飛機的 v 建立 source 到 (v, in, 1) 的邊。
• 對於所有代表跑到的 v 以及所有 1 ≤ t ≤ T 建立 (v, out, t) 到 sink 的邊。
• 對於所有 2 ≤ t ≤ T 以及所有原始圖中的邊 (v_i, v_j) 建立 (v_i, out, t - 1) → (v_j, in, t) 以及 (v_j, out, t - 1) → (v_i, in, t) 的邊。

用 dinic 做最大流的話，因為我們最多只有 T 單位的流，所以時間複雜度是 O(TE)，這裡的 E 是邊的數量。我們有 O(E) = O(nm) 以及 $O(T) = O(n)$，加上二分搜尋的時間複雜度，總複雜度會是 $O(n^2m\log{n})$。

PE

Judging from the scale of n, an O(n²) algorithm is sufficient. So it's not hard to guess that doing flood fill to check for each room's size would be the last step. Follow that instinct we need to do discretization in O(n²) to prepare for the flood fill. That turns out to be possible. One way of discretization is to create a 2n × 2n map. Observed that there is only O(n) walls, we can use O(n) time to register each wall on the map.

We must be careful to not count those non-enclosed areas. This may be done by carefully designed flood fill (e.g. special return value when out of bound) or by mark out the outside area before doing the flood fill.

An O(2n × 2n) algorithm could pass the tests but we can solve this task in O(n × n) instead. The key observation is that the x values we need to consider are the ones which have vertical lines on it. So, only n x values and n y values need to be considered during the discretization. I was planned to make O(2n × 2n) solutions TLE but Dreamoon stopped me.

從 n 的大小我們可以知道 O(n²) 的演算法足以通過。可以猜到最後一步可以用 flood fill 的方法來枚舉每個房間。依據這個直覺，我們可以得出必須要在 O(n²) 的時間內離散化的結論。事實上這是可行的，甚至因為只有 O(n) 道牆壁，所以我們對於每道牆壁可以花 O(n) 的時間來把它轉化到離散的地圖上。

我們要小心不要數到那些沒有被完整包圍的區域，一個可能的方法是在 flood fill 的時候小心處理 (例如在超出邊界時採用不同的回傳值)，另外一個方法是在開始 flood fill 前先把所有外圍的區域標記起來。

O(2n × 2n) 的演算法可以通過測試，不過其實我們可以做到 O(n × n)。一個關鍵的觀察是，我們只需要考慮那些有垂直牆壁的 x 座標，所以我們在離散化時所考慮的 x 跟 y 座標可以只有 n 個。我本來想讓 O(2n × 2n) 的作法 TLE，但是 Dreamoon 阻止了我。