I found the following derivation using Lagrange multipliers for the solution of the Core Training problem in Code Jam this year. I liked this approach particularly because I don't get to use Lagrange multipliers very often in programming competitions.

Let 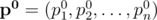denote the initial vector of success probabilities that we are given, and let 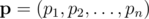be an arbitrary vector of success probabilities. Let 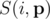denote the probability of exactly i cores succeeding given that the success probabilities in 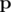. Then we are trying to maximise

subject to

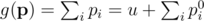
By using the Lagrangian method, we get that an optimal solution must satisfy

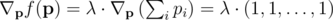
or it must be on the boundary (but we'll get to that later).

Lemma

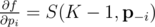
where 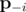is the vector of probabilities with p_i removed, i.e. (p₁, p₂, ..., p_i - 1, p_i + 1, ..., p_n). That is, the partial derivative of f with respect to p_i is the probability that exactly K - 1 of the cores succeed, not including core i itself.

Proof of Lemma

This is a somewhat well-known derivation, but I have included it for completeness. By expanding the terms,

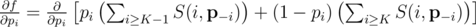
which simplifies to

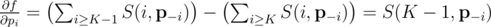
(End proof.)

In order to have 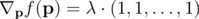, then the most obvious thing to do is to set all the p_i equal to each other. However this is not possible, since we cannot reduce p_i below p⁰_i. By taking into account boundary conditions, this then gives us three choices for each core i:

1. We leave p_i at its initial value p⁰_i.
2. We increase p_i to 1.
3. We try to equalise p_i with the some other {p_j} that are not on the boundary.

This observation is sufficient to restrict the solution space to the point where we can search over it. (Well, we still need to make some efficiency arguments, like "only increase p_i up to 1 if it is already big", and "only try to equalize p_i's that are close to each other", etc..., but you get the idea.)