First, I really need to apologize for the round. There was a serious problem in D that was even covered in the sample test, that the main solution did not handle correctly. I should have been much more careful with this problem and looked for these kind of cases. Unfortunately, it was a big enough issue that caused the round to be unrated. I know this upset a lot of people, but it's tricky to find a solution to this kind of problem after the problem has happened.

I still hope the problems were good quality. If you learned something new from the round, or from this editorial, then the round was worth it. I would advise to solve the problems you couldn't solve during the contest, so you can take away something from the round.

821A — Okabe and Future Gadget Laboratory

We can simulate exactly what's described in the statement: loop over all cells not equal to 1 and check if it doesn't break the city property. To check if a cell breaks the property, just loop over an element in the same row, and an element in the same column, and see if they can add to give the cell's number. The complexity is O(n⁴).

#include <queue>
#include <vector>
#include <list>
#include <map>
#include <set>
#include <deque>
#include <stack>
#include <bitset>
#include <algorithm>
#include <functional>
#include <numeric>
#include <utility>
#include <sstream>
#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <ctime>
#include <complex>
#include <fstream>
#include <cstring>
#include <string>
#include <climits>
using namespace std;
//macros
typedef long long ll;
typedef complex<double> point;
typedef pair<int,int> ii;
typedef vector<int> vi;
typedef vector< vector<int> > vvi;




#define FOR(k,a,b) for(int k=(a); k<=(b); ++k)
#define REP(k,a) for(int k=0; k<(a);++k)
#define SZ(a) int((a).size())
#define ALL(c) (c).begin(),(c).end()
#define PB push_back
#define MP make_pair
#define INF 999999999
#define INFLONG 1000000000000000000LL
#define MOD 1000000007
#define MAX 100
#define ITERS 100
#define pi 3.1415926
#define MAXN 100000
#define _gcd __gcd

int main()
{
    int n;
    cin >> n;
    int grid[50][50];
    REP(i,n){
        REP(j,n){
            cin >> grid[i][j];
        }
    }
    REP(i,n){
        REP(j,n){
            if(grid[i][j]==1) continue;
            bool pass = false;
            for(int r = 0;r<n;r++){
                if(r==i) continue;
                for(int c = 0; c < n; c++){
                    if(c==j) continue;
                    int sum = grid[r][j]+grid[i][c];
                    if(sum==grid[i][j]){
                        pass=true;
                        break;
                    }
                }
                if(pass)break;
            }
            if(!pass){
                cout << "No"<<endl;
                return 0;
            }
        }
    }
    cout << "Yes"<<endl;
}

821B — Okabe and Banana Trees

The critical observation to make is that the optimal rectangle should always have a lower-left vertex at the origin. This is due to the fact that the line has positive y-intercept and negative slope: any rectangle which doesn't have a vertex at the origin could easily be extended to have a vertex at the origin and even more bananas.

Then, we just need to try every x-coordinate for the upper-right corner of the box and pick the maximum y-coordinate without going over the line. We can compute the sum of any rectangle in O(1) using arithmetic series sums, so this becomes O(bm) because the x-intercept can be up to bm. You can make it faster by trying every y-coordinate; this makes the complexity O(b), but this was unnecessary to solve the problem.

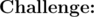Can you solve the problem with better complexity?

#include <queue>
#include <vector>
#include <list>
#include <map>
#include <set>
#include <deque>
#include <stack>
#include <bitset>
#include <algorithm>
#include <functional>
#include <numeric>
#include <utility>
#include <sstream>
#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <ctime>
#include <complex>
#include <fstream>
#include <cstring>
#include <string>
#include <climits>
using namespace std;

//macros
typedef long long ll;
typedef complex<double> point;
typedef pair<int,int> ii;
typedef vector<int> vi;
typedef vector< vector<int> > vvi;




#define FOR(k,a,b) for(int k=(a); k<=(b); ++k)
#define REP(k,a) for(int k=0; k<(a);++k)
#define SZ(a) int((a).size())
#define ALL(c) (c).begin(),(c).end()
#define PB push_back
#define MP make_pair
#define INF 999999999
#define INFLONG 1000000000000000000
#define MOD 1000000007
#define MAX 100
#define ITERS 100
#define MAXM 200000
#define MAXN 1000000
#define _gcd __gcd
#define eps 1e-9
ll series(ll x){
	return x*(x+1)/2;
}
int main() {
	int m,b;
	cin >> m >> b;
	ll best = 0;
	for(int y = b; y >=0; y--){
		//y = -x/m + b
		ll x = m*(b-y);
		ll t = 0;
		t+=(x+1)*series(y)+(y+1)*series(x);
		best = max(best,t);
	}
	cout << best << endl;
}

821C — Okabe and Boxes

It looks like Daru should only reorder the boxes when he has to (i.e. he gets a remove operation on a number which isn't at the top of the stack). The proof is simple: reordering when Daru has more boxes is always not worse than reordering when he has less boxes, because Daru can sort more boxes into the optimal arrangement. Therefore, our greedy algorithm is as follows: simulate all the steps until we need to reorder, and then we resort the stack in ascending order from top to bottom.

This has complexity O(n² log n). However, we can speed this up if we note that whenever we reorder boxes, any box currently on the stack can be put in an optimal position and we can pretty much forget about it. So whenever we reorder, we can just clear the stack as well and continue. This gives us O(n) complexity because every element is added and removed exactly once.

#include <vector>
#include <utility>
#include <iostream>
#include <cassert>
#include <map>
#include <climits>
#include <deque>
#include <algorithm>
#include <set>
#include <stack>
using namespace std;

#define ll long long
#define REP(i,a) for(int i = 0; i < (a); i++)
#define PB push_back
#define SZ(a) (a).size()
#define MP make_pair
#define ALL(a) (a).begin(),(a).end()
#define fs first
typedef vector<int> vi;
typedef pair<int,int> pii;



int main()
{
    int n;
    cin >> n;
    stack<int> st;
    int curr=1;
    int ans = 0;
    REP(i,2*n){
        string str;
        cin >> str;
        assert(str[0]=='a' || str[0]=='r');
        if(str[0]=='a'){
            int x;
            cin >> x;
            st.push(x);
        }else if(str[0]=='r'){
            if(!st.empty()){
                if(st.top()==curr){ //last thing added is what we need to remove
                    st.pop();
                }else{ //last thing we added is NOT what we need to remove
                    ans++;
                    while(!st.empty()) st.pop(); //clears the stack
                }
            }
            curr++;
        }
    }
    cout << ans << endl;
}

821D — Okabe and City

First, let's make this problem into one on a graph. The important piece of information is the row and column we're on, so we'll create a node like this for every lit cell in the grid. Edges in the graph are 0 between 2 nodes if we can reach the other immediately, or 1 if we can light a row/column to get to it. Now it's a shortest path problem: we need to start from a given node, and with minimum distance, reach another node.

Only problem is, number of edges can be large, causing the algorithm to time out. There are a lot of options here to reduce number of transitions. The easiest one I found is Benq's solution, which I'll describe here. From a given cell, you can visit any adjacent lit cells. In addition, you can visit any lit cell with difference in rows at most 2, and any lit cell with difference in columns at most 2. So from the cell (r,c), you can just loop over all those cells.

The only tricky part is asking whether the current lit row/column should be a part of our BFS state. Since we fill the entire row/col and can then visit anything on that row/col, it doesn't matter where we came from. This means that you can temporarily light each row/column at most once during the entire BFS search.

So complexity is O(n + m + k), with a log factor somewhere for map or priority queue. Interestingly enough, you can remove the priority queue log factor because the BFS is with weights 0 and 1 only, but it performs slower in practice.

Benq's code: ~~~~~ /*#include <ext/pb_ds/assoc_container.hpp>

include <ext/pb_ds/tree_policy.hpp>*/

include <bits/stdc++.h>

using namespace std; //using namespace __gnu_pbds;

typedef long long ll; typedef vector vi; typedef pair<int, int> pii; //typedef tree<int,null_type,less,rb_tree_tag,tree_order_statistics_node_update> ordered_set;

define FOR(i, a, b) for (int i=a; i<b; i++)

define F0R(i, a) for (int i=0; i<a; i++)

define FORd(i,a,b) for (int i = (b)-1; i >= a; i--)

define F0Rd(i,a) for (int i = (a)-1; i >= 0; i--)

define mp make_pair

define pb push_back

define f first

define s second

define lb lower_bound

define ub upper_bound

const int MOD = 1000000007; double PI = 4*atan(1);

int dr[10001], dc[10001]; vi row[10001], col[10001]; priority_queue todo; vector lights; int dist[10001]; map<pii,int> label; int xdir[4] = {1,0,-1,0}, ydir[4] = {0,1,0,-1}; int n,m,k;

void filrow(int i, int val){ if (i >= 1 && i <= n && dr[i] == 0) { dr[i] = 1; for (int x: row[i]) if (val < dist[x]) { dist[x] = val; todo.push({-dist[x],x}); } } }

void filcol(int i, int val) { if (i >= 1 && i <= m && dc[i] == 0) { dc[i] = 1; for (int x: col[i]) if (val < dist[x]) { dist[x] = val; todo.push({-dist[x],x}); } } }

void ad(int x, int y, int val) { if (label.find({x,y}) != label.end()) if (dist[label[{x,y}]] > val) { dist[label[{x,y}]] = val; todo.push({-val,label[{x,y}]}); } }

int main() { cin >> n >> m >> k;

F0R(i,k) {
    int r,c; cin >> r >> c;
    lights.pb({r,c});
    row[r].pb(i);
    col[c].pb(i);
    label[{r,c}] = i;
}

F0R(i,10001) dist[i] = MOD;

if (label.find({n,m}) == label.end()) {
    filrow(n-1,1);
    filrow(n,1);
    filcol(m-1,1);
    filcol(m,1);
} else todo.push({0,label[{n,m}]});


while (todo.size()) {
    auto a = todo.top(); todo.pop();
    a.f = -a.f;
    if (a.f > dist[a.s]) continue;

    F0R(i,4) ad(lights[a.s].f+xdir[i],lights[a.s].s+ydir[i],a.f);
    FOR(i,lights[a.s].f-2,lights[a.s].f+3) filrow(i,a.f+1);
    FOR(i,lights[a.s].s-2,lights[a.s].s+3) filcol(i,a.f+1);
}

if (dist[0] != MOD) cout << dist[0];
else cout << -1;

} ~~~~~

821E — Okabe and El Psy Kongroo

You can get a naive DP solution by computing f(x, y), the number of ways to reach the point (x, y). It's just f(x - 1, y + 1) + f(x - 1, y) + f(x - 1, y - 1), being careful about staying above x axis and under or on any segments.

To speed it up, note that the transitions are independent of x. This is screaming matrix multiplication! We can make a 16x16 matrix, where the entry (i,j) is 1 if we can go from y value of i to y value of j in one move. You can build this quickly and then matrix exponentiate for under every segment, then carry the DP values of the end of that segment over to start the next segment. This gives complexity O(nh³ log w) where h = 16 and w = k.

#include <queue>
#include <vector>
#include <list>
#include <map>
#include <set>
#include <deque>
#include <stack>
#include <bitset>
#include <algorithm>
#include <functional>
#include <numeric>
#include <utility>
#include <sstream>
#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <ctime>
#include <complex>
#include <fstream>
#include <cstring>
#include <string>
#include <climits>
#include <chrono>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <assert.h>
using namespace std;

//macros
typedef long long ll;
typedef complex<double> point;
typedef pair<int,int> ii;
typedef vector<int> vi;
typedef vector< vector<int> > vvi;




#define FOR(k,a,b) for(int k=(a); k<=(b); ++k)
#define REP(k,a) for(int k=0; k<(a);++k)
#define SZ(a) int((a).size())
#define ALL(c) (c).begin(),(c).end()
#define PB push_back
#define MP make_pair
#define INF 1000000001
#define INFLONG 1000000000000000000
#define MOD 1000000007
#define MAX 100
#define ITERS 100
#define MAXM 200000
#define MAXN 1000000
#define _gcd __gcd
#define EPS 1e-7
#define PI 3.1415926535897932384626
#define ERR -987654321

//multiplies m1 and m2 and stores in m3
vector<vector<long long> > matmul(vector<vector<long long> > m1, vector<vector<long long> > m2, vector<vector<long long> > &m3){
    m3.clear();
    vector<vector<long long> > ans;
    REP(i,SZ(m1)){
        vector<long long> v;

        REP(j,SZ(m2[0])){
            v.PB(0);
        }
        ans.PB(v);
    }

    REP(r,SZ(m1)){
        REP(c,SZ(m2[0])){
            REP(k, SZ(m2)){
                ans[r][c] += m1[r][k]*m2[k][c];
                ans[r][c]%=MOD;
            }
        }
    }

    REP(i,SZ(m1)){
        vector<long long> cur;
        REP(j,SZ(m2[0])){
            cur.PB(ans[i][j]);
        }
        m3.PB(cur);
    }
    return m3;


}
vector<ll> mymul(vector<ll> vec, vector<vector<ll> > mat, vector<ll> &ret){
    vector<ll> res;
    REP(i,SZ(vec)){
        ll sum = 0;
        for(int co = 0; co < SZ(mat); co++){
            sum += vec[co]*mat[co][i];
            sum%=MOD;
        }
        res.PB(sum);
    }
    ret.clear();
    REP(i,SZ(res)) ret.PB(res[i]);
    return ret;
}
void printmat(vector<vector<long long> > matr){
    REP(i,SZ(matr)){
        REP(j,SZ(matr[i])){
            cout << matr[i][j] << " " ;
        }
        cout << endl;
    }
}
vector<vector<long long> > matexp(vector<vector<long long> > matr, long long n){
    vector<vector<long long> > ans;
    REP(i,SZ(matr)){
        vector<long long> v;
        REP(j,SZ(matr[0])){
            v.PB((i==j));
        }
        ans.PB(v);
    }
    long long t = n;

    while(t>0){

        if(t%2==0){
            matmul(matr,matr,matr);
            t/=2;
        }
        else{
            matmul(ans,matr,ans);
            t--;
        }
    }

    return ans;
}

int main()
{
    int n;
    ll k;
    cin >> n >> k;
    vector<ll> a1,a2,b;
    REP(i,n){
        ll a1r, a2r, br;
        cin >> a1r >> a2r >> br;
        a1.PB(a1r);
        a2.PB(a2r);
        b.PB(br);
    }
    vector<ll> ans;
    ans.PB(1);
    a2[SZ(a2)-1] = k;
    REP(i,n){
        //update ans size
        while(SZ(ans) < b[i]+1) ans.PB(0);
        while(SZ(ans) > b[i]+1) ans.erase(prev(ans.end()));
        vector<vector<ll> > trans;
        int len = b[i]+1;
        REP(pr,len){
            vector<ll> lol;
            REP(pro,len){
                lol.PB(0);
            }
            trans.PB(lol);
        }
        REP(co,len){
            if(co>0) trans[co-1][co] = 1;
            trans[co][co] = 1;
            if(co+1<len) trans[co+1][co] = 1;
        }
        mymul(ans,matexp(trans,a2[i]-a1[i]),ans);
    }
    cout << ans[0] << endl;
}