A div2 - Равенство
Иначе искомая величина равна <span class="tex-span"><i>max</i>(0, <i>k</i> - <i>d</i>)</span>, где <span class="tex-span"><i>d</i></span> -- количество различных букв в исходной строке.
Это верно, потому что, в случае, когда <span class="tex-span"><i>k</i> ≤ <i>d</i></span>, необходимость в изменениях отсутствует. Если же <span class="tex-span"><i>d</i> < <i>k</i> ≤ |<i>s</i>|</span>, то можно заменить <span class="tex-span"><i>k</i> - <i>d</i></span> букв, которые встречаются более одного раза, на буквы, которых в <span class="tex-span"><i>s</i></span> нет.
<\spoiler> Сложность решения: 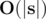
B div2 - Прямоугольники
Пройдемся по каждой строке и по каждому столбцу, посчитаем количество клеток <span class="tex-span"><i>k</i><sub class="lower-index">0</sub>, <i>k</i><sub class="lower-index">1</sub></span> соответствующих цветов.
Просуммируем для всех полученных <span class="tex-span"><i>k</i><sub class="lower-index"></sub> * </span> функцию <span class="tex-span">2<sup class="upper-index"><i>k</i><sub class="lower-index"></sub> * </sup> - 1</span> (это число непустых подмножеств данного цвета, целиком лежащих в конкретной строке/столбце).
В конце необходимо вычесть из полученной суммы <span class="tex-span"><i>n</i>·<i>m</i></span> -- количество одноклеточных множеств, которые мы посчитали два раза (один раз в строке и один раз в столбце).
Сложность решения: $\mathbf{O(n \cdot m)}
A div1 / C div2 - Сортировка подпоследовательностями
Разобьем <span class="tex-span"><i>P</i></span> на простые циклы. Тогда качестве ответа можно взять подпоследовательности, образованные этими простыми циклами.
Больше подпоследовательностей сделать нельзя, так как сортировка подпоследовательности -- это также перестановка, и, если бы последователность <span class="tex-span"><i>a</i><sub class="lower-index"><i>i</i></sub></span> можно было бы разбить на большее число подпоследовательностей, то существовало бы разбиение перестановки <span class="tex-span"><i>P</i></span> на большее число простых циклов.
Сложность решения: <img align="middle" class="tex-formula" src="https://espresso.codeforces.com/a5ef278204454b0d7840c823cb7775fe832c248d.png" style="max-width: 100.0%;max-height: 100.0%;" />
B div1 / D div2 - Интерактивный LowerBound
Будем идти из нее по порядку по элементам списка, пока не встретим первый элемент больший или равный x, который и будет ответом.
Вероятность того, что этот алгоритм за 2000 действий не найдет нужный элемент равна вероятности того, что среди 1000 предыдущих перед правильным ответом элементов списка не встретится ни одного, который попал в нашу выборку из 999 случайных элементов. Эту вероятность можно оценить как (1 - 999 / n)1000 ≈ 1.7·10 - 9\
C div1 / E div2 - Переподвешивание дерева
Компоненты, которые крепятся к центроиду, не могут поменять свой центроид или разделиться. За (размер компоненты * 2) можно превратить ее в ёжик (например превратить ее вначале в бамбук, а потом в ёжик), подвешенный к её центроиду. Доказательство того, что сумму квадратов расстояний меньше сделать нельзя, оставим в качестве дополнительного упражнения для пытливых читателей.\\
Сложность решения: <img align="middle" class="tex-formula" src="https://espresso.codeforces.com/a5ef278204454b0d7840c823cb7775fe832c248d.png" style="max-width: 100.0%;max-height: 100.0%;" />
D div1 - Динамический кратчайший путь
E div1 - Максимальный поток
Для каждого ребра исходного графа, по которому ничего не течет создадим ребро в том же направлении с <span class="tex-span"><i>f</i> = <i>INF</i></span> пропускной способностью. Для каждого ребра, по которому что-то течет создадим два ребра, одно в том же направлении с <span class="tex-span"><i>f</i> = 1</span>, и одно в обратном c <span class="tex-span"><i>f</i> = <i>INF</i></span>.
В новой сети найдем минимальный разрез, он будет состоять только из ребер с <span class="tex-span"><i>f</i> = 1</span>, соответствующие им ребра исходного графа и будут искомым минимальным набором.
Если бы минразрез оказался равен бесконечности, то описание, которое нам дали в условии не могло бы быть описанием максимального потока, он был бы гарантированно увеличиваемым.
Теперь достаточно построить ненулевой поток по всем ребрам, по которым это требуется в условии и сделать <span class="tex-span"><i>c</i> = <i>f</i></span> на ребрах, которые мы решили сделать насыщенными, и <span class="tex-span"><i>c</i> = <i>f</i> + 1</span> на всех остальных. Рассмотрим ориентированный граф ребер, по которым что-то должно течь. \\
\textbf{Лемма:} \textit{каждое ребро этого графа либо лежит на цикле, либо лежит на пути из истока в сток. В первом случае можно пустить по циклу циркуляцию <span class="tex-span">1</span>, во втором пустить по пути из истока в сток поток <span class="tex-span">1</span>. Таким образом, по каждому ребру, по которому должно что-то течь, будет что-то течь.}
\textbf{Доказательство леммы:} Предположим обратное. Возьмем такое ребро <span class="tex-span"><i>u</i></span>-><span class="tex-span"><i>v</i></span>. Значит, либо нет пути из <span class="tex-span"><i>s</i></span> в <span class="tex-span"><i>u</i></span>, либо нет пути из <span class="tex-span"><i>v</i></span> в <span class="tex-span"><i>t</i></span>. Пусть верно второе без ограничения общности. Рассморим множество вершин достижимых из <span class="tex-span"><i>v</i></span>. Если там есть <span class="tex-span"><i>u</i></span>, то нашелся цикл. Если нет, то это множество плохое, потому что в нем нет <span class="tex-span"><i>t</i></span>, в него что-то втекает и ничего не вытекает, в корректной сети такого быть не может.






