Let's not what in case k > |s|, we should always print <>.

Overwise the finding value is equal max(0, k - d), where d -- count of different letters in original string.

Let's note at first, that each set of cells always situated only in one row or column.

We should go through every row and every column and count of k₀ and k₁ cells. For every k *  we will summarize 2^k * - 1 (the count of non-empty subsets of this color).

At the end we subtract n·m from all sum (this is the count of one-cell sets, witch we get twice).

The difficulty of solution: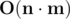

Sorting any sequence means applying some permutation to its elements. All the elements of sequence a are different, therefore this permutation is unique and fixed. Let's call it P.

We can split this permutation into simple cycles. The subsequences in the answer are subsequences formed by these simple cycles.

It's easy to see that it's impossible to split the sequence into more subsequences because if we could split the sequence into more subsequences, we also could split permutation P into more cycles.

Let's ask the values ​​in cell start and in 999 other random cells, choose among them the largest among those whose value is less than or equal to x.

Let's go from it in order to the elements of the list, until we meet the first element greater or equal to x, which will be the answer.

The probability that this algorithm for 2000 of actions will not find the desired element is equal to the probability that among the 1000 of the previous before the correct answer of the list elements there will not be one that has got to our sample of 999 random elements. This probability can be estimated as (1 - 999 / n)¹⁰⁰⁰ ≈ 1.7·10^- 9

The centroid-vertex remains in such operations a centroid. If we have two centroids in a tree, the edge between them is permanent. The components that are attached to the centroid can not change their centroid or separate. For (the size of the component * 2), you can turn it into a hedgehog (for example, turn it firstly into bamboo, and then into a hedgehog) suspended from its centroid. The proof that the sum of squares of distances couldn't be less can be left as an additional exercise for inquisitive readers The difficulty of the solution: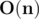

Firstly, let's run an usual Dijkstra from s, find distances and make them a potentials of vertices. Then for each request let's recalculate all distances and make the potentials equal to these distances. To quickly recalculate the distance between requests, we can use the fact that in a graph with potentials, all distances are 0. When we increased the weight of some edges by 1, in the graph with potentials, all distances do not exceed the number of changed edges so we can run a Dijkstra on a vector per O(V + E).

At first, let's find minimal set of saturated edges. For this we will make new flow network with same set of vertices, but with little bit different edges.

For each edge from original graph without any float let's create new edge with the same direction with a f = INF carrying capacity. For every edge with a float let's create two edges with the same direction with f = 1 capacity and one edge with reversed direction with f = INF.

In the new network we have to find the minimum cut, it will consist of edges with f = 1, corresponding to them edges of a graph will be a wanted minimal set.

If this minimal set was equal to infinity the description of the task wouldn't be about maximum float, because it had to be increasing for sure.

So now it's enough to create non-zero float for all edges needed in the task and to make c = f on edges which we chose to be saturated and c = f + 1 on the rest. Let's consider tan oriented graph with edges with a float.

A lemma: Every edge of a graph lies either on a cycle or on the way from source to flow. In the first situation we might make a circulation on a cycle 1, in the second situation we can put a float on the way from the source to the stream of 1. Thus, for each edge on which something is to flow, something will flow

The proof: Suppose the converse. Let's take the edge of the form u->v. Well then, there are no way from s to u or no way from v to t. Let the second be true without loss of generality. Let's consider the set of vertices attainable from v. If there are u in this set, there is a cycle. If there are no u, this set is "bad", cause there are no t, in it something flows in and nothing follows, in a correct network this can not be.