Привет, Codeforces! Сегодня мы попробуем решить пару задач на целочисленный бинпоиск по ответу с помощью std::lower_bound и поймем, что это бессмысленно, но красиво (на самом деле нет).

Начнем с задачи 535C - Tavas and Karafs, которая решается двоичным поиском (например, 32799258). В этой задаче по заданным l, t, m, A, B нужно найти такое наибольшее , что

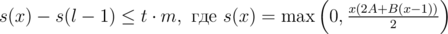
Как известно, std::lower_bound(first, last, v, pred) возвращает итератор, указывающий на первое значение a такое, что pred(a, v) == false. Если в качестве предиката использовать s(x) - s(l - 1) ≤ t·m, то ответом на задачу будет значение, предшествующее lower_bound'у.

Приступим. К качестве диапазона для бинпоиска будем использовать массив range такой, что range[i] = i. Заполнить такой массив поможет std::iota из <numeric>.

const int N = 1000000;
int range[N + 5];
//...
iota(range, range + N, 0);

lower_bound заточен под бинарные предикаты, но у нас унарный. Значит, второй аргумент будет фиктивным и искомое значение (третий параметр lower_bound) будут фиктивными. Оформим предикат в виде лямбды и получим такую функцию

inline int solve(int l, int t, int m) {
    int r = (t - A) / B + 1;
    i64 lim = i64(t)*m;
    if (r < l)            
        return -1;
    if (sum(l, l) > lim)
        return -1;
    return *lower_bound(range + l, range + r + 1, 0, [lim, l](int item, int) -> bool {
    	return sum(l, item) <= lim; //sum(l, item) - это s(item) - s(l - 1) из описания
    }) - 1;
}

Возможно, обработка случаев с -1 не требуется, но я её оставил от предыдущего решения. Полный вариант решения с lower_bound — 32800781. Время работы этого решения почти не отличается от самописного бинпоиска.

В рассмотренной задаче мы явно использовали то, что диапазон бинпоиска небольшой, и его можно целиком хранить в массиве. Но что делать, если границы имеют порядок 10⁹ или даже 10¹⁸? В этом случае придется реализовать итератор для целочисленного диапазона, использующий O(1) памяти, который удовлетворяет интерфейсу RandomAccessIterator. Например, так (много кода):

class Range {
public:
	typedef long long IntType;
	
	class iterator : public std::iterator<random_access_iterator_tag, 
		IntType, 
		IntType, 
		const IntType*, 
		IntType> {
	public:
		typedef iterator It;
		
		iterator(IntType pos)
			: pos(pos) {
		}

		//value access
		IntType operator[](IntType idx) {
			return (pos + idx);
		}

		IntType operator*() {
			return pos;
		}

		//arithmetics
		It& operator +=(IntType delta) {
			pos += delta;
			return (*this);
		}

		It& operator ++() {
			return (*this) += 1;
		}

		It operator ++(int) {
			++pos;
			return It(pos - 1);
		}

		It& operator -=(IntType delta) {
			pos -= delta;
			return (*this);
		}

		It& operator --() {
			return (*this) -= 1;
		}

		It operator --(int) {
			--pos;
			return It(pos + 1);
		}

		IntType operator -(const It& rhs) const {
			return pos - rhs.pos;
		}

		//relational
		bool operator ==(const It& rhs) const {
			return pos == rhs.pos;
		}

		bool operator != (const It& rhs) const {
			return pos != rhs.pos;
		}

		bool operator <(const It& rhs) const {
			return pos < rhs.pos;
		}

		bool operator <=(const It& rhs) const {
			return pos <= rhs.pos;
		}

		bool operator >(const It& rhs) const {
			return pos > rhs.pos;
		}

		bool operator >=(const It& rhs) const {
			return pos >= rhs.pos;
		}

	private:
		IntType pos;
	};

	Range(IntType a, IntType b)
		: a(a), b(b) {
	}

	Range()
		: Range(0, 1) {
	}
	
	iterator begin() const {
		return iterator(a);
	}

	iterator end() const {
		return iterator(b + 1);
	}

	IntType a, b;
};

Этот вариант опробуем на задаче 760B - Frodo and pillows (спасибо -Morass- за Problem Topics). В этой задаче по заданным n, m, k небходимо найти такое наибольшее 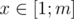, что

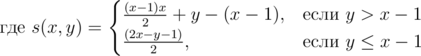
Оформим все аналогично предыдущей задаче и получим такое решение c использованием Range:

//...
typedef long long i64;

inline i64 pillows(i64 x, i64 y) {
	if (y > x — 1) {
		return (x*(x — 1)) / 2 + y — (x — 1);
	}
	return ((2*x — y — 1)*y) / 2;
}

int main() {
	i64 n, m, k;
	cin >> n >> m >> k;
	Range range(1, m);
	cout << (*lower_bound(range.begin(), range.end(), 0, [n, m, k](long long x, int) -> bool {
		return pillows(x, k &mdash; 1) + pillows(x, n &mdash; k) + x <= m; 		
	}) &mdash; 1);
	return 0;
}

Полный вариант — 32802235.

Очевидно, что вариант с Range имеет смысл только тогда, когда есть возможность заинлайнить (с помощью JHelper и подобных инструментов) написанный ранее класс Range. Но в этом случае можно заинлайнить и написанный ранее шаблонизированный бинпоиск, получив исходник меньшего размера и более (хоть и незначительно) производительный бинпоиск. Таким образом, практическое применение lower_bound в задачах на бинпоиск по ответу имеет смысл только при небольшом размере диапазона.