Hint: When does some vowel stay in string?
Iterate over the string, output only consonants and vowels which don't have a vowel before them.
Hint 1: It's never profitable to go back. No prizes left where you have already gone.
Hint 2: The optimal collecting order will be: some prefix of prizes to you and the other prizes to your friend (some suffix).
You can find the total time with the knowledge of the prefix length. The final formula is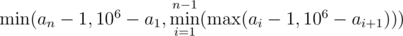 
.
Hint: At first we will solve the problem mentioned in the statement. The formula is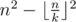 
. Firstly, each submatrix k × k should have at least one row with zero in it. Exactly 
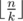non-intersecting submatrices fit in matrix n × k. The same with the columns. So you should have at least this amount squared zeros.
Now that you know the formula, you can iterate over n and find the correct value. The lowest non-zero value you can get for some n is having k = 2. So you can estimate n as about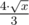 
.
Now let's get k for some fixed n.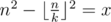 
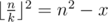
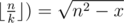
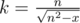. Due to rounding down, it's enough to check only this value of k.
The function of the path length is not that different from the usual one. You can multiply edge weights by two and run Dijkstra in the following manner. Set disti = ai for all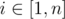 
and push these values to heap. When finished, disti will be equal to the shortest path.
Подсказка 1: Посчитайте, сколько раз каждое число встречается в сумме всех fa.
Подсказка 2: Попробуйте подобрать точные критерии того, что ai войдет в fa для какой-либо перестановки.
Подсказка 3: Докажите, что ai входит тогда и только тогда, когда все элементы до нее строго меньше (кроме максимума в массиве). Теперь попробуйте решить за O(n2).
Попытайтесь упростить решение и сделать его быстрее.
Легко заметить, что i-й элемент входит в fa тогда и только тогда, когда все элементы до нее строго меньше, поэтому если определим li как количество элементов меньших ai, то ответ будет равен:
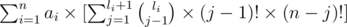
Взглянем на позицию ai, если он на позиции j, то требуется выбрать j - 1 из li меньших элементов, расставить их каким-то образом и расставить остальные. Можем найти все li за O(n log n). Если написать ровно это, то асимптотика будет O(n2).
Попробуем улучшить формулу. Раскроем как:
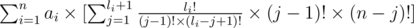
теперь это равно:
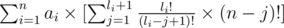
и вынесем li!,
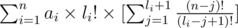
теперь домножим первую сумму на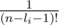 
и вторую сумму на (n - li - 1)!, оно становится равно:
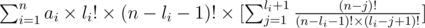
и легко заметить, что это же равно:
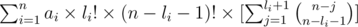
Используем тот факт, что
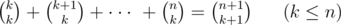
это равно:
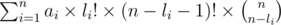
Тогда окончательный ответ равен:
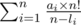
который может быть легко посчитан за O(n log n). Не забудьте, что считать ответ для максимального числа не нужно.
Также есть другое решение, которое можно прочитать тут.
В разборе обозначим n = |s|.
Подсказка: Есть простое решение за время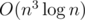 
: dp[m][mask] — лучший ответ, если мы рассмотрели первые m символов строки, а маска обозначает, подстроки какой длины мы удаляли. Однако хранить строку в каждом состоянии не позволяют ни ограничения по времени, ни ограничения по памяти. Как можно улучшить это решение?
Давайте попробуем улучшить это решение при помощи жадных соображений. Так как каждое состояние обозначает возможный префикс строки-результата, то среди двух состояний dp[m1][mask1] и dp[m2][mask2] с одинаковыми длинами ответа, но разными ответами, нам не нужно рассматривать то, в котором ответ лексикографически больше. Поэтому для каждой возможной длины префикса существует только одна лучшая строка, которую стоит рассматривать в качестве префикса результата. А значит, в динамике можно просто хранить \t{bool} — можем ли мы достичь такого состояния с лучшим ответом или нет.
Такую динамику необходимо считать особым образом, перебирая длину префикса результирующей строки. При фиксированной длине префикса сначала обработаем все переходы с удалением подстрок (так как они не добавляют нового символа), а затем среди всех позволяющих достичь этой длины состояний dp[m][mask], для которых dp[m][mask] = true, мы выбираем лучший символ, позволяющий перейти к следующей длине префикса (а переход из состояния делается по (m + 1)-му символу строки).
Сложность этого решения 
, но оно на самом деле достаточно быстрое.
Это усложнённая версия задачи G с Educational Round 27. Её разбор можно найти здесь.
Чтобы решить нашу текущую задачу, воспользуемся известным методом динамической связности. Построим дерево отрезков по запросов: каждая вершина ДО будет содержать список всех рёбер, присутствующих в графе на соответствующем отрезке запросов. Если некоторое ребро присутствует с запроса l по запрос r, то его можно добавить по аналогии с прибавлением на отрезке [l, r] в ДО (но вместо прибавления мы вставляем ребро в список, и мы не делаем никаких проталкиваний, которые обычно делаются в ДО с отложенными операциями). Если мы теперь напишем некоторую структуру, которая может добавлять ребро и откатывать изменения, можно решить задачу, обойдя дерево отрезков обходом в глубину: когда мы входим в вершину, добавим все рёбра в списке этой вершины; когда мы в листе, посчитаем ответ для запроса в этом листе (если он там есть); и когда мы покидаем вершину, мы откатываем сделанные в ней изменения.
Какая структура данных нам понадобится? Во-первых, DSU с поддержкой расстояния до лидера (чтобы находить \textit{некоторый} путь между двумя вершинами). Не стоит использовать сжатие путей, из-за откатов оно не будет ускорять операции в DSU.
Во-вторых, надо как-то поддерживать базис циклов в графе (так как граф всегда связный, то нет смысла поддерживать базис циклов для каждой компоненты отдельно). Удобный способ хранения базиса — использовать массив из 30 элементов, изначально заполненный нулями (обозначим этот массив как a). i-элемент массива будет обозначать некоторое число в базисе, в котором i-й бит является максимальным среди всех взведённых битов. Тогда можно очень просто добавить в базис некоторое число x: переберём все биты от 29-го до 0-го, и если некоторый бит j равен 1 в числе x, и a[j] ≠ 0, то присвоим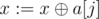 
(назовём этот процесс \textit{сокращением}, он нам ещё потребуется). Если после этого мы получим 0, то число уже является линейной комбинацией базиса; иначе, пусть k — наибольший бит, равный 1 в x, нам нужно просто присвоить a[k]: = x.
Такой способ хранения базиса также позволяет очень просто отвечать на запросы 3 типа: сначала возьмём длину пути из DSU (пусть эта длина равна p), а затем просто \textit{сократим} p, и это и будет ответом.
