This article is an English translation of the NOIP Round 1 (the Qualification Round) problems. Here are some backgrounds about it.

• matthew99 has written an Introduction to Chinese OI contests, but he ignored this for some reason; maybe this exam is too easy for him in his province.
• It is literally a "preliminary contest".
• Basically, this is a qualification round for NOIP.
• This is a written examination.
• The exam lasts for 2 hours.
• The total score is 100. You may need to get ~80 scores (in provinces like Zhejiang) or ~20 scores (in provinces like Inner Mongolia) to pass.
• This translation may be not 100% exact, but you can feel the flavor of the NOIPR1.

In part IV and V, the translator modified and formatted the source codes with clang-format .

Part I: Single Choice Problems

2 score for each problem.

1.

In the following four numbers in different positional notation, which one is different from the other three?

• A. (269)16
• B. (617)10
• C. (1151)8
• D. (1001101011)2

2.

Which of the following programming language is run by a interpreter?

• A. C
• B. C++
• C. Pascal
• D. Python

3.

When did Chinese Computer Federation found the NOI competitions? (it was called "National High School Students' Computer Programming Contest")

• A. 1983
• B. 1984
• C. 1985
• D. 1986

4.

Define the depth of a single node to be 0. What is the number of nodes of a full k-ary tree of depth h?

• A. (k^h + 1 - 1) / (k - 1)
• B. k^h - 1
• C. k^h
• D. (k^h - 1) / (k - 1)

5.

There is an algorithm whose time-cost function is T(n) = T(n - 1) + n, T(0) = 1. What is its time complexity?

• A.
• B.
• C. O(n)
• D. O(n²)

6.

What is the prefix form (Polish notation) of the expression a*d-b*c?

• A. a d * b c * -
• B. - * a d * b c
• C. a * d - b * c
• D. - * * a d b c

7.

Choose two points A and B randomly on a segment of length 1. What's the expected length of |AB| ?

• A. 1 / 2
• B. 1 / 3
• C. 2 / 3
• D. 3 / 5

8.

Catalan Numbers is C_n = (2n)! / (n + 1)! / n! . Which of the following is wrong?

• A. C_n = the number of different binary trees of n+1 nodes
• B. C_n = the number of legal bracket sequence of length 2n
• C. C_n = the number of possible "pop sequence" if we push 1,2,...,n into a stack
• D. C_n = the number of ways to triangulate a convex (n+2)-gon

9.

Assume there is a machine with a button. Whenever you push that button, it will randomly give you either a red ball or a blue ball with 1/2 probability each. Infinitively many people play with this machine. Each of them push that button until a blue ball is given. Then they will put all their balls into a big box. Let U be the number of blue balls in the box and R be the number of red balls. What is U:R?

• A. 1 : 2
• B. 2 : 1
• C. 1 : 3
• D. 1 : 1

10.

You need to write a code to compute the number of 1's in the binary form of a natural number n.

Here is the code:

int CountBit(int x)
{
    int ret = 0;
    while (x)
    {
        ret++;
        ________;
    }
    return ret;
}

What should you fill in the blank?

• A. x >>= 1
• B. x &= x - 1
• C. x |= x >> 1
• D. x <<= 1

Part II: Multiple Choice Problems

There are several choices in each problem. No less than one of them is correct. You must find them all to get 2 score for each problem in this part.

11.

What can you take into the exam room in NOIP Round 1?

• A. Pen or Pencil
• B. Eraser
• C. Mobile phone (turned off)
• D. Draft paper

12.

The 2-3 tree is a special kind of rooted trees. They satisfy:

1. all non-leaf nodes have 2 or 3 children;
2. all leaf has the same depth.

If a 2-3 tree have 10 leaves, how many non-leaf nodes may it have?

• A. 5
• B. 6
• C. 7
• D. 8

13.

Which of the following statements are true?

• A. if there is no negative cycle but negative edges in a graph, Dijkstra's algorithm may not calculate the single source shortest paths
• B. if there is no negative edge, calling Dijkstra's algorithm multiple times may calculate the shortest paths between any pair of nodes
• C. if there is negative cycles, you can call Dijkstra's algorithm one time to calculate single source shortest paths
• D. when there is no negative edge, calling Dijkstra's algorithm once cannot be used to calculate the shortest paths between any pair of nodes

14.

Which of the following properties do a tree have?

• A. there is no cycle
• B. there is only one simple path between any pair of nodes
• C. have and only have one simple cycle
• D. the number of edges equals to the number of nodes minus one

15.

Which of the following statements about the Turing Award are true?

• A. it is set up by Institute of Electrical and Electronics Engineers (IEEE)
• B. the only Chinese who has got the Award is Yao Qizhi
• C. its name is from the pioneer of computer science, the British scientist Alan Mathison Turing
• D. it's the most famous and most honored award in computer field. It was honored as the "Nobel Prize in computer field".

Part III: Problem Solving

5 score for each task.

Task 1

There are four friends. let's call them Jia, Yi, Bing and Ding. They are deciding whether they will go out for a hike.

1. if it rains and Yi doesn't go out, then Jia will not go out;
2. if Yi goes out, then Ding will go out;
3. if Bing goes out, Ding must not go out;
4. if Ding doesn't go out and Jia doesn't go out, then Bing won't go out.

Now you can see Bing is going out. So:

• Does Jia go out?
• Does Yi go out?
• Does Ding go out?
• Is it raining? The last problem is 2 scores; the other 1 score.

Task 2

How many pairs of solution does the equation a*b = (a and b)*(a or b) have when a,b are integers in range [0,31]? (* means multiplication, and, or are bitwise operations)

Part IV: Read the Source Code and Write the Output

8 scores for each task.

Task 1

#include <cstdio>
int main() {
  int x;
  scanf("%d", &x);
  int res = 0;
  for (int i = 0; i < x; ++i) {
    if (i * i % x == 1) {
      ++res;
    }
  }
  printf("%d", res);
  return 0;
}

The input is: 15

What's the output?

Task 2

#include <cstdio>
int n, d[100];
bool v[100];
int main() {
  scanf("%d", &n);
  for (int i = 0; i < n; ++i) {
    scanf("%d", d + i);
    v[i] = false;
  }
  int cnt = 0;
  for (int i = 0; i < n; ++i) {
    if (!v[i]) {
      for (int j = i; !v[j]; j = d[j]) {
        v[j] = true;
      }
      ++cnt;
    }
  }
  printf("%d\n", cnt);
  return 0;
}

The input is: 10 7 1 4 3 2 5 9 8 0 6

What's the output?

Task 3

#include <iostream>
using namespace std;
string s;
long long magic(int l, int r) {
  long long ans = 0;
  for (int i = l; i <= r; ++i) {
    ans = ans * 4 + s[i] - 'a' + 1;
  }
  return ans;
}
int main() {
  cin >> s;
  int len = s.length();
  int ans = 0;
  for (int l1 = 0; l1 < len; ++l1) {
    for (int r1 = l1; r1 < len; ++r1) {
      bool bo = true;
      for (int l2 = 0; l2 < len; ++l2) {
        for (int r2 = l2; r2 < len; ++r2) {
          if (magic(l1, r1) == magic(l2, r2) && (l1 != l2 || r1 != r2)) {
            bo = false;
          }
        }
      }
      if (bo) {
        ans += 1;
      }
    }
  }
  cout << ans << endl;
  return 0;
}

The input is: abacaba

What's the output?

Task 4

#include <cstdio>
using namespace std;
const int N = 110;
bool isUse[N];
int n, t;
int a[N], b[N];
bool isSmall() {
  for (int i = 1; i <= n; ++i)
    if (a[i] != b[i])
      return a[i] < b[i];
  return false;
}
bool getPermutation(int pos) {
  if (pos > n) {
    return isSmall();
  }
  for (int i = 1; i <= n; ++i) {
    if (!isUse[i]) {
      b[pos] = i;
      isUse[i] = true;
      if (getPermutation(pos + 1)) {
        return true;
      }
      isUse[i] = false;
    }
  }
  return false;
}
void getNext() {
  for (int i = 1; i <= n; ++i) {
    isUse[i] = false;
  }
  getPermutation(1);
  for (int i = 1; i <= n; ++i) {
    a[i] = b[i];
  }
}
int main() {
  scanf("%d%d", &n, &t);
  for (int i = 1; i <= n; ++i) {
    scanf("%d", &a[i]);
  }
  for (int i = 1; i <= t; ++i) {
    getNext();
  }
  for (int i = 1; i <= n; ++i) {
    printf("%d", a[i]);
    if (i == n)
      putchar('\n');
    else
      putchar(' ');
  }
  return 0;
}

The first input is: 6 10 1 6 4 5 3 2

The second input is: 6 200 1 5 3 4 2 6

What are the outputs?

Part V: Program Blank Fill-in

In this part, you are given several programs with their descriptions, but some expressions in the programs are deleted. Fill in the blanks to make the programs work as described.

Task 1

You have a 1-indexed permutation P of length n. We define array Q as: Q_i is the smallest j satisfying 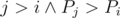. If such j doesn't exist, Q_i = n + 1 .

For example, if n = 5, P = {1, 5, 4, 2, 3}, then Q = {2, 6, 6, 5, 6}.

The following program reads P and calculates Q with double-linked list. It is guaranteed that n ≤ 10⁵.

#include <iostream>
using namespace std;
const int N = 100010;
int n;
int L[N], R[N], a[N];
int main() {
  cin >> n;
  for (int i = 1; i <= n; ++i) {
    int x;
    cin >> x;
    /*fill in(1)*/;
  }
  for (int i = 1; i <= n; ++i) {
    R[i] = /*fill in(2)*/;
    L[i] = i - 1;
  }
  for (int i = 1; i <= n; ++i) {
    L[/*fill in(3)*/] = L[a[i]];
    R[L[a[i]]] = R[/*fill in(4)*/];
  }
  for (int i = 1; i <= n; ++i) {
    cout << /*fill in(5)*/ << " ";
  }
  cout << endl;
  return 0;
}

Task 2

Piggy wants to buy n objects. n ≤ 1000. He can choose from two shops, A and B.

Each of these n objects are sold in both shops. If Piggy buy the i-th object at A shop, the cost is a[i]. If Piggy buy the i-th object at B shop, the cost is b[i]. All the prices are no less than 0 and no more than 10000. If the total price in shop A is no less than 50000, everything Piggy buy at A shop will have a 5% discount. That is, if total_a >= 50000, result = total_a * 0.95 + total_b.

Calculate the minimum amount of money does Piggy need to buy the n objects.

#include <cstdio>
#include <algorithm>
using namespace std;
const int Inf = 1000000000;
const int threshold = 50000;
const int maxn = 1000;
int n, a[maxn], b[maxn];
bool put_a[maxn];
int total_a, total_b;
double ans;
int f[threshold];
int main() {
  scanf("%d", &n);
  total_a = total_b = 0;
  for (int i = 0; i < n; ++i) {
    scanf("%d%d", a + i, b + i);
    if (a[i] <= b[i])
      total_a += a[i];
    else
      total_b += b[i];
  }
  ans = total_a + total_b;
  total_a = total_b = 0;
  for (int i = 0; i < n; ++i) {
    if (/*fill in(1)*/) {
      put_a[i] = true;
      total_a += a[i];
    } else {
      put_a[i] = false;
      total_b += b[i];
    }
  }
  if (/*fill in(2)*/) {
    printf("%.2f", total_a * 0.95 + total_b);
    return 0;
  }
  f[0] = 0;
  for (int i = 1; i < threshold; ++i)
    f[i] = Inf;
  int total_b_prefix = 0;
  for (int i = 0; i < n; ++i)
    if (!put_a[i]) {
      total_b_prefix += b[i];
      for (int j = threshold - 1; j >= 0; --j) {
        if (/*fill in(3)*/ >= threshold && f[j] != Inf)
          ans = min(ans, (total_a + j + a[i]) * 0.95 + /*fill in(4)*/);
        f[j] = min(f[j] + b[i], j >= a[i] ? /*fill in(5)*/ : Inf);
      }
    }
  printf("%.2f", ans);
  return 0;
}

The answer is here.