Basically the title. The problem statement can be found here. No idea how to solve it efficiently.
UPDATE 1: why the downvotes?
UPDATE 2: based on the answers so far, the solution would be to exhaustively explore all combinations of exponents k1, k2, ..., kr (ki ≥ kj for all i < j) such that 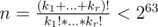 and k = 2k1 * 3k2 * 5k3 * 7k4 * 11k5 * ... < 263. During the exhaustive search one can map each n to its minimum k found (for instance, using an unordered_map) and then the queries can be answered in O(1). The problem is: how can you estimate the complexity of the exhaustive search? Any easy way to estimate an upperbound for it?
and k = 2k1 * 3k2 * 5k3 * 7k4 * 11k5 * ... < 263. During the exhaustive search one can map each n to its minimum k found (for instance, using an unordered_map) and then the queries can be answered in O(1). The problem is: how can you estimate the complexity of the exhaustive search? Any easy way to estimate an upperbound for it?
UPDATE 3: pshishod2645 says there are around 2 * 106 valid combinations of exponents, where did he get that number from?






