Hello Codeforcers! As a student of department of mathematics, I'd like to demonstrate an application of Extended Field.
The idea of Extended Field
First we should include the idea of splitting field, a splitting field F of a polynomial P is the smallest field such that
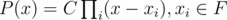
I use the word "smallest" with the sense that if P split over E, 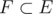 .
.
In the other word, P decomposes into linear factor under it's splitting field.
Example
P = x2 + 1 does not split over
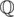 but split over
but split over 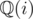 where
where 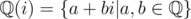 which is widely used as complex.
which is widely used as complex.Let p = 998244353 = 7 * 17 * 223 + 1, P = x224 - 1 does not split over
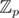 but split over
but split over 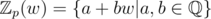 where
where 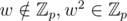 . The multiplication order ord(w2) = 223.
. The multiplication order ord(w2) = 223.Let p = 109 + 7, Fibonacci number can be easily written as
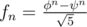 . Where φ, ψ are both root of
. Where φ, ψ are both root of 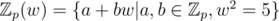 (Remark that x2 = 5 has no root in Z_p)
(Remark that x2 = 5 has no root in Z_p)
Problem Solving
The problem to be demonstrated is 718C - Саша и массив, which corresponds to the third example. (This may be not the best solution for the problem. I've got several TL on this problem for large constant on module.)
In the problem, we should handle Fibonacci number 1, 1, 2, 3, 5, 8, ... with the formula 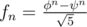 . Once we have decompose the Fibonacci into two sequence of number powers. The problem becomes.
. Once we have decompose the Fibonacci into two sequence of number powers. The problem becomes.
My implementation
We can implement Extended Field using C++ class, just like complex:
template<int sq = 5, int MOD = 1000000007>
class EX {
int re, im;
static int trim(int a) {
if (a >= MOD) a -= MOD;
if (a < 0) a += MOD;
return a;
}
static int inv(const int a) {
int ans = 1;
for (int cur = a, p = MOD - 2; p; p >>= 1, cur = 1ll * cur * cur % MOD) {
if (p&1) ans = 1ll * ans * cur % MOD;
}
return ans;
};
public:
EX(int re = 0, int im = 0) : re(re), im(im) {}
EX& operator=(EX oth) { return re = oth.re, im = oth.im, *this; }
int norm() const {
return trim((1ll * re * re - 1ll * sq * im % MOD * im) % MOD);
}
EX conj() const {
return EX(re, trim(MOD - im));
}
EX operator*(EX oth) const {
return EX((1ll * re * oth.re + 1ll * sq * im % MOD * oth.im) % MOD,
(1ll * re * oth.im + 1ll * im * oth.re) % MOD);
};
EX operator/(int n) const {
return EX(1ll * re * inv(n) % MOD, 1ll * im * inv(n) % MOD);
}
EX operator/(EX oth) const { return *this * oth.conj() / oth.norm(); }
EX operator+(EX oth) const { return EX(trim(re + oth.re), trim(im + oth.im)); }
EX operator-(EX oth) const {
return EX(trim(re - oth.re), trim(im - oth.im));
}
EX pow(long long n) const {
EX ans(1);
for (EX a = *this; n; n >>= 1, a = a * a) {
if (n&1) ans = a * ans;
}
return ans;
}
bool operator==(EX oth) const { return re == oth.re and im == oth.im; }
bool operator!=(EX oth) const { return not (*this == oth); }
int real() const& { return re; }
int imag() const& { return im; }
};
Once a splitting field implementation is done, we can FFT under Zp more than. I haven't implemented it yet.






