I would like to invite you all to the International Coding Marathon 2019, under the banner of Technex'19, IIT (BHU) Varanasi.
Technex is the annual techno-management fest of Indian Institute of Technology (BHU), Varanasi organized from March 8 — 10, 2019.
International Coding Marathon is the flagship event of Byte The Bits, the set of programming events organized under Technex. ICM is brought to you by Mentor Graphics. It will take place on Friday, 8th March 2019, 21:00 IST. The contest will be held on Codechef.
The problemset has been prepared by hitman623, dhirajfx3, _shanky, drastogi21 and me (Enigma27). We would like to express our heartiest thanks to _hiccup and prakhar28 for their constant help in preparing the contest.

Prizes -
Overall 1st — INR 15,000
Overall 2nd — INR 10,000
India 1st — INR 9,000
India 2nd — INR 5,000
IIT(BHU) 1st — INR 6,000
IIT(BHU) 2nd — INR 4,000
IIT(BHU) Freshmen 1st — INR 1,000
Some of our previous contests :
ICM Technex 2017 and Codeforces Round #400 (Div. 1 + Div. 2, combined)
ICM Technex 2018 and Codeforces Round #463 (Div. 1 + Div. 2, combined)
Participants will have 2 hours 30 minutes to solve 7 problems. The scoring will be ICPC style.
Good luck everyone! Hope to see you on the leaderboard.
UPD — Contest begins in 1.5 hours
UPD1 — Contest begins in 15 minutes
UPD2 — Contest has ended. Congratulations to the winners. They will be contacted soon.
We deeply regret the inconvenience caused due to the problem ICM03. We will try to avoid such things in the future.
Editorials will be uploaded soon. Feel free to discuss the problems in the comment section.
The answer array has to have N elements and K distinct elements.
Thus, choose K distinct elements to be from 1 to K and remaining N - K elements to be 1.
The sum of which is : (K * (K + 1) / 2) + N - K
Let P[i] be the difference between the number of days Bob studied and the number of days he didn't till ith day.
Thus, we have to ensure that P[i] > = 0 for 1 < = i < = N.
Iterate over all i and greedily flip 0 to 1 whenever P[i] becomes negative.
Let us consider an array of N elements b, consisting of 0 and 1, 0 denotes Snorlax doesn't work out on the ith day and 1 indicates that he does.
The window size is K.
Let us look at the ith window, when you slide one window further, from the subarray sum, we have to subtract b[i] and add b[i + k]. Effectively adding b[i + k] - b[i]. If this value is 1, we can surely say that b[i] is 0 and b[i + k] is 1 and if this value - 1, the reverse is true.
If this difference is 0, we can say that b[i] and b[i + k] are equal but can't tell the exact values.
If the absolute value of this difference is more than 1, array construction is impossible.
Note that, we thus get relations between b[i], b[i + k], b[i + 2k]... and so on. We just check if these relations are consistent. If we just know any of this group, we can figure out the rest of this group. Note that part of a group are those indices who have same remainder on division with l.
At an index, we cannot get more than 1 invalid value. Meaning, we can't say that b[i] is neither 0 nor 1.
There is still one constraint we haven't enforced yet and this is the sum of the values in 1st window, till now, we only looked the difference between consecutive windows.
We enforce this constraint by making 1 those values that are unknown and occur at the end of the 1st window (the end because we have to minimise the number of 1's too and the ending values have the largest remainders, it can easily be seen that those with large remainder occur fewer times than those with smaller remainder).
If we are unable to enforce the above constraint, then also making the array is impossible.
The complexity is O(N).
Let us first represent each cell with a number by 2d[i][j]. For a grid to be palindrome, the xor of all values should have at max 1 set bit in it. For a grid to be divisible by 6, the sum of digits should be divisible by 3 and the grid should contain at least 2 even digits.
A corner case is when the grid consists of only a single element. [6] is the only single element grid possible.
Since, N * M < = 100000, min(N, M) < = 320 Lets suppose N < = M, otherwise we can flip the grid diagonally and answer wont change. Lets iterate over 2 rows i and j. Let us store prefix_sums, prefix_xors and prefix_even_nos for the columns considering all rows from i to j. Let us iterate over the rightmost column k.
Now, all l's such that
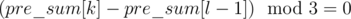
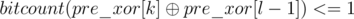
(pre_even[k] - pre_even[l - 1]) > = 2
are valid leftmost columns of the grid.
For the third condition we can use 2 pointers. For first and second conditions, we can store frequency of xors along with 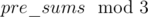 in a [1«10][3] array and run an extra 9 size loop for second condition.
in a [1«10][3] array and run an extra 9 size loop for second condition.
So, overall complexity will be O(min(N, M) * N * M * 10). Refer to the code for better understanding.
#include <bits/stdc++.h>
#define int long long
#define pb push_back
#define pii pair<int,int>
#define vi vector<int>
#define vii vector<pii>
#define mi map<int,int>
#define mii map<pii,int>
#define all(a) (a).begin(),(a).end()
#define x first
#define y second
#define sz(x) (int)x.size()
#define endl '\n'
#define hell 1000000007
#define rep(i,a,b) for(int i=a;i<b;i++)
using namespace std;
int n,m;
int ans;
vector<string> s;
vector<vi> colsum,colxor,coleven;
int prexor[1<<10][3],curxor[100005],cursum[100005],cureven[100005];
void solve(){
cin>>n>>m;
s.resize(n+1);
rep(i,1,n+1){
cin>>s[i];
s[i]='#'+s[i];
}
if(n>m){
rep(i,1,n+1) s[i].resize(n+1);
rep(i,1,n+1){
rep(j,i,n+1){
swap(s[i][j],s[j][i]);
}
}
swap(n,m);
}
colsum.resize(m+1);
colxor.resize(m+1);
coleven.resize(m+1);
rep(i,1,m+1){
colsum[i].resize(n+1);
colxor[i].resize(n+1);
coleven[i].resize(n+1);
rep(j,1,n+1){
colsum[i][j]=(colsum[i][j-1]+s[j][i]-'0')%3;
colxor[i][j]=(colxor[i][j-1]^(1<<(s[j][i]-'0')));
coleven[i][j]=coleven[i][j-1]+((s[j][i]-'0')%2==0);
}
}
rep(i,1,n+1){
rep(j,i,n+1){
for(int k=0;k<(1<<10);k+=2) prexor[k][0]=prexor[k][1]=prexor[k][2]=0;
rep(k,1,m+1) curxor[k]=curxor[k-1]^colxor[k][j]^colxor[k][i-1];
rep(k,1,m+1) cursum[k]=(cursum[k-1]+colsum[k][j]-colsum[k][i-1]+3)%3;
rep(k,1,m+1) cureven[k]=cureven[k-1]+coleven[k][j]-coleven[k][i-1];
int lo=0;
rep(k,1,m+1){
while(lo<k and cureven[k]-cureven[lo]>=2){
prexor[curxor[lo]][cursum[lo]]++;
lo++;
}
ans+=prexor[curxor[k]][cursum[k]];
rep(l,1,10) ans+=prexor[curxor[k]^(1<<l)][cursum[k]];
}
}
}
rep(i,1,n+1){
rep(j,1,m+1){
if(s[i][j]=='6'){
ans++;
}
}
}
cout<<ans<<endl;
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t=1;
// cin>>t;
while(t--){
solve();
}
return 0;
}
There are different ways to solve this problem. One is using a square-root trick as follows:
Run binary search over the maximum weight used. To check if a given maximum weight is valid we need to find the sum of weights from U to V with weight less than a given weight. This can be done by breaking the path in three parts : U to root, V to root and LCA(u, v) to root.
sum(U, V, W) = sum(U, root, W) + sum(V, root, W) - 2 * sum(lca, root, W) + (w[lca] < W) * w[lca]
So, we want to find the sum of weights less than W on a path from a node U to root.
Let’s divide the tree into blocks of size B and mark n / B special nodes such that any path from a node to root does not take more than B nodes until it reaches a special node.
One can do this by keeping a count of 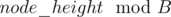 and then taking the index corresponding to the minimum value as base_height.
and then taking the index corresponding to the minimum value as base_height.
All nodes at a height h with 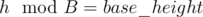 will be marked special. Hence there can be at most n / B special nodes (pigeonhole principle) and distance between a node to its closest special node is less than B.
will be marked special. Hence there can be at most n / B special nodes (pigeonhole principle) and distance between a node to its closest special node is less than B.
For each special node, store the weights in the path from root to this node in a sorted order. This can be done in a single dfs. This step will take W * (n / B) time if we sort the weights using counting sort (since the weights are bounded) where W is the upper bound for weight of nodes.
Then we can find the sum by moving up the tree until we reach a special node. For a special node, we can easily answer the query in log(n) using another binary search (upperbound/lowerbound). This step will take B + log(n) time per query.
Count of nodes can also be calculated along with the sum. We need to carefully handle the number of times nodes with maximum weight are used.
Overall time complexity is O(W * (n / B) + q * log(W) * (B + log(n))). An optimal value for B is close to 200.
Another solution is using persistent segment trees by keeping the information of root to a node in segment tree.
The maximum length of G can be K. For length > = K + 1 , all elements of G won't be distinct.
The second condition can be expressed as 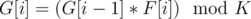
Lets make a directed graph containing K vertices from 0 to K - 1. An edge from X to Y signifies that in the sequence G, Y can come after X.
For checking if Y can come after X, we have: 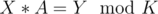 , for some A.
, for some A.
There exists some A if gcd(X, K) divides Y. This can also be written as gcd(X, K) divides gcd(Y, K). (Note that there can be multiple values of A but we have to find number of sequences for G and not for F, so it doesn't matter.)
Now, our task is to calculate the number of simple paths of length 1 to K in the graph and sum them up. Lets simplify the graph. Observe that both edges from X to Y and Y to X exist if and only if gcd(X, K) = gcd(Y, K). So, lets group the numbers from 0 to K - 1 such that in each group all the numbers have same gcd with K. Observe that the graph formed by these groups as components is a DAG. So now we can do DP to find the number of paths starting from a particular component.
Number of distinct values of gcd(i, K) are equal to the number of divisors of K. Since, K is upto 1012, the number of divisors can be upto M = 7000. So, the final graph consists of at max M nodes and C(M, 2) edges.
The path starting from a component would look like :
some non-empty sequence of elements from this component + sequence from the child components
The first part is equal to : 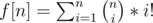 , where n is the number of elements in that component and i is the length of the chosen sequence from this part.
, where n is the number of elements in that component and i is the length of the chosen sequence from this part.
The second part would be the sum of dp values of all components reachable from current component and an extra +1 for ending at the current component only. The Final answer would be the sum of dp values of all components, as the path can start from any component.
For the first part observe that f[n]%mod = f[n%mod]. (Proof is easy).
Since, mod is upto 106, we can calculate the f values before hand, using the recurrence f[n] = n * (f[n - 1] + 1).
So, overall complexity would be O(mod + M2) where M is the number of divisors of K.
#include <bits/stdc++.h>
#define int long long
#define pb push_back
#define pii pair<int,int>
#define vi vector<int>
#define vii vector<pii>
#define mi map<int,int>
#define mii map<pii,int>
#define all(a) (a).begin(),(a).end()
#define x first
#define y second
#define sz(x) (int)x.size()
#define endl '\n'
#define hell 1000000007
#define rep(i,a,b) for(int i=a;i<b;i++)
using namespace std;
vi divisors;
int k,mod,a[10005],b[1000006],dp[10005],ans;
void solve(){
divisors.clear();
ans=0;
memset(dp,0,sizeof dp);
memset(a,0,sizeof a);
cin>>k>>mod;
b[0]=1;
rep(i,1,mod) b[i]=(i*b[i-1]+1)%mod;
for(int i=1;i*i<=k;i++){
if(k%i==0){
divisors.pb(i);
if(i*i!=k) divisors.pb(k/i);
}
}
sort(all(divisors));
for(int i=sz(divisors)-1;i>=0;i--){
a[i]=k/divisors[i];
dp[i]=1;
rep(j,i+1,sz(divisors)){
if(divisors[j]%divisors[i]==0){
a[i]-=a[j];
dp[i]=(dp[i]+dp[j])%mod;
}
}
dp[i]=dp[i]*(b[a[i]%mod]-1+mod)%mod;
ans=(ans+dp[i])%mod;
}
cout<<ans<<endl;
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t=1;
cin>>t;
while(t--){
solve();
}
return 0;
}






