Recently, I was asked to help flesh out a problem for the [NAIPC 2019](http://naipc19.kattis.com) contest whose problems are also used every year as the "Grand Prix of America." Although I didn't create or invent the problem, I helped write a solution and created some of the test data for [Problem C, Cost Of Living](https://naipc19.kattis.com/problems/costofliving). ↵
↵
From the problem setter's perspective, this was intended to be an easy, A-level problem: suppose you have an table of values $a_{y,c}$ that meet the condition that: $a_{y, c} = b_c m_c^y \prod_{k<y} i_k$ for some $m_c > 0$. ↵
↵
If you are given a subset of the values in this table, and a subset of the values for $i_k$, determine whether a set of queried values $a_{y', c'}$ is uniquely determined or not. Note that $a_{0, c} = b_c$.↵
↵
Most contestants immediately realized that above product can be written as a linear combination/sum by taking the logarithm on both sides:↵
↵
$\log{a_{y, c}} = \log{b_c} + y \log{m_c} + \sum_{k<y} \log{i_k}$↵
↵
Each given value thus represents a linear equation in unknowns $\log{b_c}$, $\log{m_c}$, and $\log{i_k}$ (plus some trivial equations for the subset of $i_k$ that may be given.) On the right hand side of the system appear the logarithms of the given table values. The left hand side of the system has only integer coefficients. Each row contains $y+1$ 1's and one coefficient with value $y$.↵
↵
Each query, in turn, can also be written as a linear equation by introducing a variable $q' = \log{a_{y', c'}}$:↵
↵
$\log{b_c} + y \log{m_c} + \sum_{k<y} \log{i_k} - \log{a_{y', c'}} = 0$↵
↵
Now, all that is left is to solve for the query variables using a traditional method (Gaussian Elimination with partial pivoting) and report the results — or so we thought.↵
↵
While top teams disposed of this problem quickly, there was a great deal of uncertainty among some contestants whether this approach would work. One team attempted to solve the problem with a homegrown variant of Gaussian elimination, but got WA because their answer was too far off the requested answer (the answer had to be given with 1e-4 rel tolerance in this problem).↵
↵
When they downloaded the judge data generator scripts, they observed that the amount of error in their implementation changed when they printed the input data with higher precision, which was very confusing to them.↵
↵
For this problem, the input data was not given with full precision because it involves products with up to 20 factors. For instance, if $b_c = m_c = i_k = 1.1$ than $a_{10, c} = 6.72749994932560009201$ (exactly) but the input data would be rounded to $6.7274999493$. If they changed this and printed instead $6.72749994932561090621$ (which is what is computed when double precision floating point is used), their solution would be much closer to the expected answer. Their result became even better when they used a floating point number type that uses more bits internally, such as quad-precision floats or java.math.BigDecimal. Thus, they concluded, they were doomed to begin with because the input data was "broken".↵
↵
What could account for this phenomenon?↵
↵
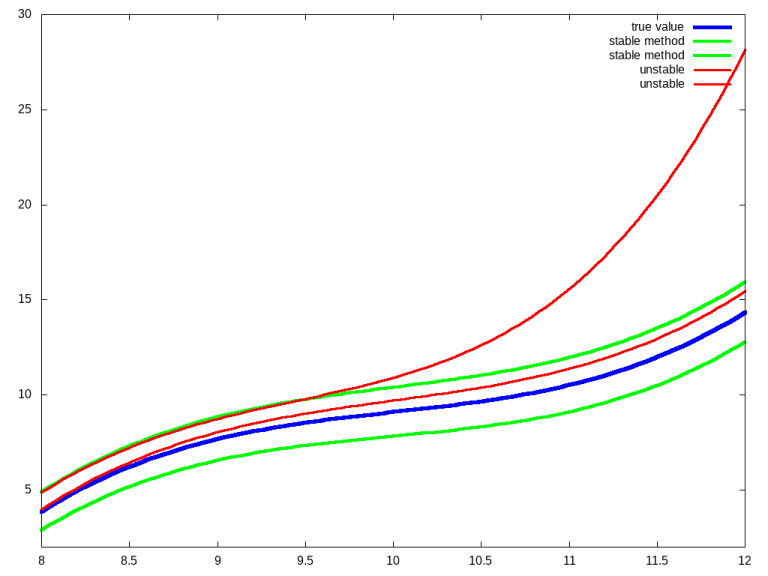
The answer lies in a property of numerical algorithm called [stability](https://en.wikipedia.org/wiki/Numerical_stability). Stability means that an algorithm does not magnify errors (approximations) in the input data; instead, the error in the output is dampened and can be bounded by some factor.↵
The illustration below shows a simplified example:↵
↵
↵
↵
A stable algorithm will produce a bounded error even when starting with approximated input, whereas an unstable method will produce a small output error only for very small input errors.↵
↵
The particular homegrown variant of Gaussian elimination they had attempted to implement avoided division on the left-hand side, keeping all coefficients in integers, which meant that the coefficients could grow large. On the right hand side, this led to an explosive growth in cancellation which increased the relative error in the input manifold — in some cases, so large that transformation back via exp produced values outside of what can be represented with double precision (i.e., positive infinity). It was particularly perplexing to them because they had used integers intentionally in an attempt to produce a better and more accurate solution.↵
↵
Naturally, the question then arose: how could the problem setters be confident that the problem they posed could be solved with standard methods in a numerically stable fashion?↵
↵
In the course of the [discussion](http://codeforces.net/blog/entry/65500), several points of view came to light. Some contestants believed that there's a "95% percent chance" that Gaussian elimination is unstable for at least one problem input, some believed that the risk of instability had increased because the problem required a transform into the log domain and back, some believed that Gaussian problems shouldn't be posed if they involve more than 50 variables, and some contestants thought that Gaussian elimination with partial pivoting was a "randomly" chosen method.↵
↵
In short, there was a great deal of fear and uncertainty, even among otherwise experienced contestants (based on the CF ratings).↵
↵
Here are a few facts regarding Gaussian elimination with partial pivoting contestants should know:↵
↵
- Gaussian elimination (with partial pivoting) is almost always stable in practice, according to standard textbooks.↵
For instance, [Trefethen and Bau](https://www.amazon.com/Numerical-Linear-Algebra-Lloyd-Trefethen/dp/0898713617) write: ↵
_(...) Gaussian elimination with partial pivoting is utterly stable in practice. (...) In fifty years of computing, no matrix problems that excite an explosive instability are known to have arisen under natural circumstances._ ↵
Another textbook, [Golub and van Loan](https://www.amazon.com/Computations-Hopkins-Studies-Mathematical-Sciences/dp/1421407949), writes: _(...) the consensus is that serious element growth in Gaussian elimination with partial pivoting is extremely rare. The method can be used with confidence. (emphasis in the original text)_↵
↵
- The stability of Gaussian elimination depends solely on the elements in the coefficient matrix (it does not depends on any transformations performed on the right-hand side). Different bounds are known, a commonly cited bounds due to Wilkinson states that if Gaussian solves the system $(A + E) y = b$ (which implies a bound on the backward error), then $||E||_{\infty} \le 8 n^{3} G ||A||_{\infty} u + O(u^2)$ where $||E||_{\infty}$ denotes the [maximum absolute row sum norm](http://mathworld.wolfram.com/MaximumAbsoluteRowSumNorm.html). $G$ is the growth factor, defined as the maximum value for the elements $|u_{i, j}| \le G$ arising in the upper-triangular matrix of the decomposition $P A = L U$ induced by the algorithm. $u$ is the machine precision, or machine round-off error (sometimes referred to as $\epsilon$.) ↵
Intuitively, this means that Gaussian is stable unless $||A||_{\infty}$ is very large or serious growth occurs in the divisors used in the algorithm. ↵
The growth factor $G$ can be as large as $2^{n-1}$, leading to potentially explosive instability. In fact, such matrices can be constructed (there's even a Matlab package for it, [gfpp](http://www.math.sjsu.edu/~foster/gfpp.m))↵
↵
- However, it was not until ca. 1994 that matrices that arose in some actual problems were found for which Gaussian with partial pivoting was found to be unstable. See [Foster 1994](http://www.math.sjsu.edu/~foster/geppfail.pdf) and [Wright 1994](https://pdfs.semanticscholar.org/e8bc/c738629dde68ae294424d46de2d1116c0320.pdf). Perhaps unsurprisingly, those matrices look (superficially at least) similar to the classic case pointed out by Wilkinson earlier: lower triangular matrices with negative coefficients below the diagonals.↵
↵
What does this mean for programming contests?↵
↵
- First, your primary intuition should be that Gaussian elimination with partial pivoting _will_ solve the problem, not that it _won't_.↵
↵
- Second, focus on what matters: the coefficients/structure of the matrix, not the values on the right-hand side. ↵
↵
- Third, make sure you do use partial pivoting. There are numerous implementations out there in various teams' hackpacks. For instance, [Stanford ICPC](https://github.com/jaehyunp/stanfordacm/blob/master/code/ReducedRowEchelonForm.cc) or [e-maxx.ru](http://e-maxx.ru/algo/linear_systems_gauss). ↵
Do not try to be clever and roll your own.↵
↵
Overall, this graphic sums it up: when faced with a linear system of equations, you should↵
↵
↵
↵
↵
↵
From the problem setter's perspective, this was intended to be an easy, A-level problem: suppose you have an table of values $a_{y,c}$ that meet the condition that: $a_{y, c} = b_c m_c^y \prod_{k<y} i_k$ for some $m_c > 0$. ↵
↵
If you are given a subset of the values in this table, and a subset of the values for $i_k$, determine whether a set of queried values $a_{y', c'}$ is uniquely determined or not. Note that $a_{0, c} = b_c$.↵
↵
Most contestants immediately realized that above product can be written as a linear combination/sum by taking the logarithm on both sides:↵
↵
$\log{a_{y, c}} = \log{b_c} + y \log{m_c} + \sum_{k<y} \log{i_k}$↵
↵
Each given value thus represents a linear equation in unknowns $\log{b_c}$, $\log{m_c}$, and $\log{i_k}$ (plus some trivial equations for the subset of $i_k$ that may be given.) On the right hand side of the system appear the logarithms of the given table values. The left hand side of the system has only integer coefficients. Each row contains $y+1$ 1's and one coefficient with value $y$.↵
↵
Each query, in turn, can also be written as a linear equation by introducing a variable $q' = \log{a_{y', c'}}$:↵
↵
$\log{b_c} + y \log{m_c} + \sum_{k<y} \log{i_k} - \log{a_{y', c'}} = 0$↵
↵
Now, all that is left is to solve for the query variables using a traditional method (Gaussian Elimination with partial pivoting) and report the results — or so we thought.↵
↵
While top teams disposed of this problem quickly, there was a great deal of uncertainty among some contestants whether this approach would work. One team attempted to solve the problem with a homegrown variant of Gaussian elimination, but got WA because their answer was too far off the requested answer (the answer had to be given with 1e-4 rel tolerance in this problem).↵
↵
When they downloaded the judge data generator scripts, they observed that the amount of error in their implementation changed when they printed the input data with higher precision, which was very confusing to them.↵
↵
For this problem, the input data was not given with full precision because it involves products with up to 20 factors. For instance, if $b_c = m_c = i_k = 1.1$ than $a_{10, c} = 6.72749994932560009201$ (exactly) but the input data would be rounded to $6.7274999493$. If they changed this and printed instead $6.72749994932561090621$ (which is what is computed when double precision floating point is used), their solution would be much closer to the expected answer. Their result became even better when they used a floating point number type that uses more bits internally, such as quad-precision floats or java.math.BigDecimal. Thus, they concluded, they were doomed to begin with because the input data was "broken".↵
↵
What could account for this phenomenon?↵
↵
The answer lies in a property of numerical algorithm called [stability](https://en.wikipedia.org/wiki/Numerical_stability). Stability means that an algorithm does not magnify errors (approximations) in the input data; instead, the error in the output is dampened and can be bounded by some factor.↵
The illustration below shows a simplified example:↵
↵
↵
↵
A stable algorithm will produce a bounded error even when starting with approximated input, whereas an unstable method will produce a small output error only for very small input errors.↵
↵
The particular homegrown variant of Gaussian elimination they had attempted to implement avoided division on the left-hand side, keeping all coefficients in integers, which meant that the coefficients could grow large. On the right hand side, this led to an explosive growth in cancellation which increased the relative error in the input manifold — in some cases, so large that transformation back via exp produced values outside of what can be represented with double precision (i.e., positive infinity). It was particularly perplexing to them because they had used integers intentionally in an attempt to produce a better and more accurate solution.↵
↵
Naturally, the question then arose: how could the problem setters be confident that the problem they posed could be solved with standard methods in a numerically stable fashion?↵
↵
In the course of the [discussion](http://codeforces.net/blog/entry/65500), several points of view came to light. Some contestants believed that there's a "95% percent chance" that Gaussian elimination is unstable for at least one problem input, some believed that the risk of instability had increased because the problem required a transform into the log domain and back, some believed that Gaussian problems shouldn't be posed if they involve more than 50 variables, and some contestants thought that Gaussian elimination with partial pivoting was a "randomly" chosen method.↵
↵
In short, there was a great deal of fear and uncertainty, even among otherwise experienced contestants (based on the CF ratings).↵
↵
Here are a few facts regarding Gaussian elimination with partial pivoting contestants should know:↵
↵
- Gaussian elimination (with partial pivoting) is almost always stable in practice, according to standard textbooks.↵
For instance, [Trefethen and Bau](https://www.amazon.com/Numerical-Linear-Algebra-Lloyd-Trefethen/dp/0898713617) write: ↵
_(...) Gaussian elimination with partial pivoting is utterly stable in practice. (...) In fifty years of computing, no matrix problems that excite an explosive instability are known to have arisen under natural circumstances._ ↵
Another textbook, [Golub and van Loan](https://www.amazon.com/Computations-Hopkins-Studies-Mathematical-Sciences/dp/1421407949), writes: _(...) the consensus is that serious element growth in Gaussian elimination with partial pivoting is extremely rare. The method can be used with confidence. (emphasis in the original text)_↵
↵
- The stability of Gaussian elimination depends solely on the elements in the coefficient matrix (it does not depends on any transformations performed on the right-hand side). Different bounds are known, a commonly cited bounds due to Wilkinson states that if Gaussian solves the system $(A + E) y = b$ (which implies a bound on the backward error), then $||E||_{\infty} \le 8 n^{3} G ||A||_{\infty} u + O(u^2)$ where $||E||_{\infty}$ denotes the [maximum absolute row sum norm](http://mathworld.wolfram.com/MaximumAbsoluteRowSumNorm.html). $G$ is the growth factor, defined as the maximum value for the elements $|u_{i, j}| \le G$ arising in the upper-triangular matrix of the decomposition $P A = L U$ induced by the algorithm. $u$ is the machine precision, or machine round-off error (sometimes referred to as $\epsilon$.) ↵
Intuitively, this means that Gaussian is stable unless $||A||_{\infty}$ is very large or serious growth occurs in the divisors used in the algorithm. ↵
The growth factor $G$ can be as large as $2^{n-1}$, leading to potentially explosive instability. In fact, such matrices can be constructed (there's even a Matlab package for it, [gfpp](http://www.math.sjsu.edu/~foster/gfpp.m))↵
↵
- However, it was not until ca. 1994 that matrices that arose in some actual problems were found for which Gaussian with partial pivoting was found to be unstable. See [Foster 1994](http://www.math.sjsu.edu/~foster/geppfail.pdf) and [Wright 1994](https://pdfs.semanticscholar.org/e8bc/c738629dde68ae294424d46de2d1116c0320.pdf). Perhaps unsurprisingly, those matrices look (superficially at least) similar to the classic case pointed out by Wilkinson earlier: lower triangular matrices with negative coefficients below the diagonals.↵
↵
What does this mean for programming contests?↵
↵
- First, your primary intuition should be that Gaussian elimination with partial pivoting _will_ solve the problem, not that it _won't_.↵
↵
- Second, focus on what matters: the coefficients/structure of the matrix, not the values on the right-hand side. ↵
↵
- Third, make sure you do use partial pivoting. There are numerous implementations out there in various teams' hackpacks. For instance, [Stanford ICPC](https://github.com/jaehyunp/stanfordacm/blob/master/code/ReducedRowEchelonForm.cc) or [e-maxx.ru](http://e-maxx.ru/algo/linear_systems_gauss). ↵
Do not try to be clever and roll your own.↵
↵
Overall, this graphic sums it up: when faced with a linear system of equations, you should↵
↵
↵
↵
↵





