Всем привет! Сегодня обнаружил, что старая статья про остатки от деления на 2^p - 1 недоступна больше по этому адресу, ее нет ни в кэше яндекса, ни в кэше гугла. В ней описывались и доказывались интересные факты о вычислении остатков от делений на числа вида 2^p - 1, а также было указано как и где они применялись. Если эта статья доступна на каком-то другом ресурсе, или вы знаете аналогичную статью, то прошу поделиться в комментариях. Ниже я кратко перескажу то, что помню, чтобы информация не потерялась, вдруг никто не найдет.

Для начала рассмотрим систему счисления по основанию 10 и остатки от деления на 9. Известен признак делимости на 9: число делится на 9, если сумма его цифр делится на 9. Например, число 936 делится на 9, так как сумма его цифр 9 + 3 + 6 = 18 делится на 9. Действительно, 936 = 104·9. Этот признак делимости следует из представления числа в десятичной системе счисления:

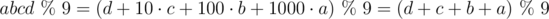
В общем случае, если число представлено в системе счисления по основанию b, то для взятия остатка от деления на b - 1 можно взять остаток от суммы его цифр, так как для любого p верно: .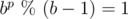

Так как в компьютерах используется двоичная система счисления, то мы можем только при помощи битовых операций брать остатки от деления на числа вида 2^p - 1, представляя числа в системе счисления по основанию 2^p. Это применяется, например, в вычислении полиномиального хеша от строк по модулям 2³¹ - 1 и 2⁶¹ - 1 — простым числам Мерсенна.

Стоит заметить, что если осуществлять только переход от числа к сумме его цифр, то мы будем получать смещенный остаток, то есть число из диапазона [1, 2^p - 1]? Чтобы этого избежать, необходимо на какой-либо итерации прибавить 1, а в конце из результата вычесть 1, чтобы сместить весь диапазон получаемых остатков от деления из [1, 2^p - 1] в [0, 2^p - 2].

Интересный вопрос: сколько раз нужно перейти от числа к его сумме для вычисления остатка от деления? Если мы представим число n в системе счисления по основанию b, то после взятия суммы его цифр, мы получим число, порядка 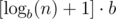, то есть, чисто интуитивно, таких редукций нужно сделать немного.

К счастью, нам не нужно считать это для каких-то абстрактных чисел n и b, посчитаем лучше, сколько нужно редукций, чтобы взять остаток от деления 64-битного числа по модулю 2³¹ - 1. Для этого нужно представить число в системе счисления по основанию 2³¹, получим: a + 2³¹·b + 2⁶²·c. Знаем, что a + b <  = 2·(2³¹ - 1), c <  = 3, получаем a + b + c <  = 2³² + 1 <  = 2³¹·2 + 1. Нам точно понадобится еще одна редукция, и тогда худшим случаем будет, когда сумма цифр данной суммы снова превысит 2³¹ - 1, и нам нужно будет сделать последнюю редукцию, получаем, что 3 — достаточно.

В качестве дополнения, ниже приведены реализации операций сложения, вычитания и умножения по модулю 2⁶¹ - 1, использующиеся в полиномиальном хеше.

typedef unsigned long long ull;

const ull MOD = (ull(1) << 61) - 1;

ull reduction(const ull a) {
// Given 0 <= a < 2^64. Need to get sum of digits in base 2^61.
    return (a & MOD) + (a >> 61);
}

ull mod(const ull a) {
// Given 0 <= a < 2^64. Need to calculate a % MOD
    return reduction(reduction(a)+1)-1;
}

ull add(ull a, const ull b) {
// Given 0 <= a, b < mod. Need to calculate (a + b) % MOD
    return (a += b) >= MOD ? (a -= MOD) : a;
}

ull sub(ull a, const ull b) {
// Given 0 <= a, b < mod. Need to calculate (a - b) % MOD
    return (a -= b) >= MOD ? (a += MOD) : a;
}

ull mul(const ull a, const ull b) {
// Given 0 <= a, b < mod. Need to calculate (a * b) % MOD
// a = a0 + a1 * 2^32
// b = b0 + b1 * 2^32
// a * b = a0 * b0 + (a0 * b1 + a1 * b0) * 2^32 + a1 * b1 * 2^64
    const ull a0 = a & ~0u, a1 = a >> 32;
    const ull b0 = b & ~0u, b1 = b >> 32;
    const ull mid = a0 * b1 + a1 * b0;
    return mod(reduction(a0 * b0) + (a1 * b1 << 3) + (mid >> 29) + (mid << 32 & MOD));
}