Доброго времени суток! Началось все с того, что после прочтения статьи про дерево Фенвика, завязал спор с товарищем Zyrax про его использование для решения задачи RMQ. Безусловно, тема не нова, но, к сожалению, статью, описывающую эту структуру данных с приведенными примерами реализации, я так и не нашел. Перед прочтением данного поста советую ознакомиться с указанной статьей, т.к. на нее будут опираться все дальнейшие рассуждения.

Встречное дерево Фенвика

Для начала, вспомним определение: Встречное дерево Фенвика (англ. counter tree Fenwick) — дерево Фенвика, в котором над каждым столбцом идет столбец такой же высоты, вычисляемый по формуле $$$f_{rev}[i]=\sum\limits_{j=i+1}^{i+2h(i)}a[j]$$$. Сразу сделаю уточнение, что под прямым деревом Фенвика подразумевается массив, посчитанный формуле: $$$f_{for}[i]=\sum\limits_{j=i-2h(i)+1}^i a[j]$$$. Для пущей понятности, прикреплю картинку.

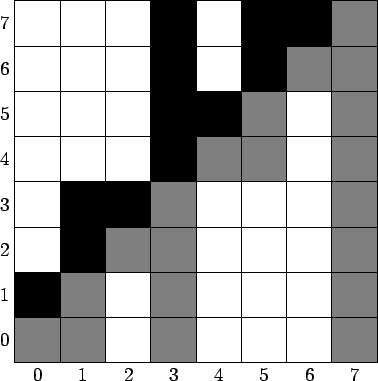
При $$$n=2^k$$$ видно, что отрезки, покрываемые прямым и обратным деревом Фенвика идентичны дереву отрезков длины n. Из этого следуют две вещи:

1. Любой отрезок делится на два других отрезка так, что один из них полностью покрывается прямым деревом Фенвика, а другой — прямым.

2. Встречное дерево Фенвика симметрично прямому.

Зная только это мы уже можем написать код для построения встречного и прямого деревьев Фенвика, где F — функция, значение которой мы хотим считать на отрезках:

void bit_build(int n, int src[]) {
	for(int i = 0; i < n; ++i) {
		a[i] = src[i]; // прямое дерево Фенвика
		b[i] = i+1 < n ? src[i+1] : NEUTRAL; // встречное дерево Фенвика
	}
	for(int i = 0, j; i < n; ++i) 
	if((j=i|i+1) < n) a[j] = F(a[i], a[j]);
	for(int i = m-n+2; i < m; ++i) {
		const int j = i|i+1;
		const int u = m-i, v = m-j;
		if(j < m) b[v] = F(b[v], b[u]);
	}
}

Остается только сопоставить получившееся дерево Фенвика и ДО. Представлю иллюстрацию для случая n=16.

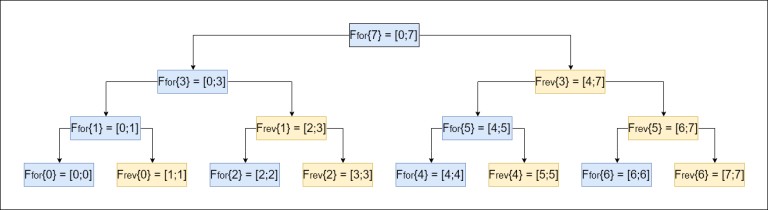
Отсюда становятся очевидными три важных факта:

1. Каждая вершина ДО (кроме листьев) составленная из элементов дерева Фенвика имеет две дочерние вершины, имеющие одинаковые индексы, но одно из них лежит в прямом дереве Фенвике, а другое в обратном.

2. В двоичной системы счисления номера листья оканчиваются на "0", вершины лежащие на втором снизу уровне обладают суффиксом "01", на третьем — "011", четвертом — "0111" и т.д.

3. Номера вершин ДО, лежащих на одном уровне, строго возрастают в порядке слева-направо.

Рассматривая номера вершин на пути от листа $$$v$$$ легко, что все вершины при их записи в двоичной системе счисления будут иметь префикс такой же, как у $$$v$$$, но суффикс будет другим, в зависимости от номера уровня, на котором лежит вершины. Для вершины номер 20.

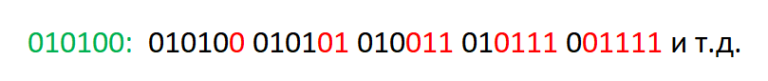
Не буду утруждать дальнейшими рассуждениями, приведу оставшиеся два участка кода, реализующие вышеописанные идеи:

// Обновление произвольного элемента в массиве
void bit_update(int id, int val) {
	if(id&1) id=id^1, b[id] = r; // в зависимости от четности обновляем значение в нужном массиве
	else              a[id] = r;
	for(int j = ~1, t=2, z=1, p=id; ; z=z|t, t=t<<1) {
		j = j^t; const int v = id&j|z; if(v >= n) break;
		// При рассмотрении следующей вершины будем учитывать, что обе дочерние вершины
		// имеют одинаковый индекс, т.е. находить их явно, нам не надо.
		if(id&t) b[v] = a[p] > b[p] ? a[p] : b[p];
		else     a[v] = a[p] > b[p] ? a[p] : b[p];
		p = v;
	}
}

// Ответ на запрос
int bit_ask(int l, int r) {
	int res = NEUTRAL;
	for(; (r&r+1) >= l && r >= l; r=(r&r+1)-1)
		if(res < a[r]) res = a[r];
	for(; (l|l-1) <= r && l && l < n; l=(l|l-1)+1) 
		if(res < b[l-1]) res = b[l-1];
	return res;
}