**[Russian version is in progress now, will be published ASAP]**↵
↵
Hello, CodeForces.↵
↵
I think that matroids are beautiful and powerful concept, however, not really well known in competitive programming.↵
↵
I’ve discovered matroids at 2019 Petrozavodsk Winter Training Camp. There was a problem that clearly cannot be solved using usual techniques I knew, editorial for this problem was just these three words “just matroid intersection”. Back then it took me more than 2 days of upsolving to find all the information and details I need and implement solution that gets AC on this. And it took way longer to actually understand why does it work and exactly how does it work. (I still hesitate in some details.)↵
↵
Of course, it is not hard to google up all the definitions and some related articles, but in my opinion they all are focused more on mathematical part of theory, strict proofs in some not really obvious but short ways, and observing only key points in whole theory, omitting a lot of intermediate results, logical steps and examples. In some article I’ve encountered this heavy-formula proof:↵
↵
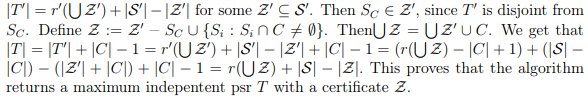↵
↵
That was nowhere close to being clear for me. (Probably I’m not mathematician enough, yet.) But still, I’m sure there is a way to make this more clear and detailed.↵
↵
I am sure, there are a lot of people in CP who will also like to get familiar with matroids. So, I’ve decided to review this topic from very beginning focusing more on explanations, logical steps and providing more examples. This is the goal of this article, and you do not need to know anything about matroids beforehand.↵
↵
[cut]↵
↵
.↵
↵
**Prerequisites.** You are not required to know well everything listed here, but it is good to be familiar with some of these concepts for better and faster understanding:↵
↵
1. Basics of set theory and set operations↵
2. Spanning trees in graphs↵
3. Matchings in bipartite graphs↵
4. Linear independence in vector spaces↵
5. Rank and basis of set of vectors↵
6. Gaussian elimination↵
7. Kruskal’s minimum spanning tree algorithm↵
8. Kuhn’s bipartite matching algorithm↵
9. Enjoying discrete math↵
↵
_All the information that used in this article is my own understanding of this topic, that I’ve learned from other articles found on the web. And as we know, proof by passing various tests is not a proper proof. So if you find something illogical or wrong, that should mean that I’ve made a mistake or misinterpret something, please point it out._↵
↵
What matroid is?↵
------------------↵
↵
Matroid is a structure that abstracts and generalizes the notion of linear independence in vector spaces.↵
↵
Here goes the formal definition. Matroid is a pair $\left\langle X, I \right\rangle$ where $X$ is called ground set and $I$ is set of all _independent_ subsets of $X$. In other words matroid $\left\langle X, I \right\rangle$ gives a classification for each subset of $X$ to be either _independent_ or _dependent_ (included in $I$ or not included in $I$).↵
↵
Of course, we are not speaking about arbitrary classifications. These $3$ properties must hold for any matroid:↵
↵
1. Empty set is independent.↵
2. Any subset of independent set is independent.↵
3. If independent set $A$ has smaller size than independent set $B$, there exist at least one element in $B$ that can be added into $A$ without loss of independency.↵
↵
These are _axiomatic properties_ of matroid. To prove that we are dealing with matroid, we generally have to prove these three properties.↵
↵
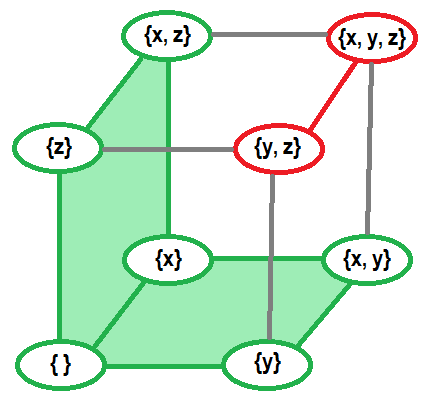
For example, explicit presentation of matroid on ground set $\\{x, y, z\\}$ which considers $\\{y, z\\}$ and $\\{x, y, x\\}$ to be dependent and marked red. Other sets are independent and marked green.↵
↵
↵
↵
From this definition we can derive some other important concepts (examples for all these concepts will be shown later, along with examples of matroids):↵
↵
**Bases.** Any independent set of maximum size is a basis of given matroid. In other words there is not element that can be added to a basis without loss of independency. All bases have equal size (otherwise we can add something to smaller basis from greater basis by third axiomatic property). Directly from previous, no basis is a subset of other basis. Any independent set is a subset of some basis (by third property we can continue increasing its size until reaching some basis), so it is enough to only know about all bases of matroid to completely describe it.↵
↵
**Circuits.** Dependent set is a circuit if all subsets (excluding whole set) of this set are independent. In other words, circuit is dependent set, that does not allow removing any of its elements without gaining independence. No circuit is a subset of another circuit (otherwise we can remove some elements from greater circuit without removing dependence). ↵
↵
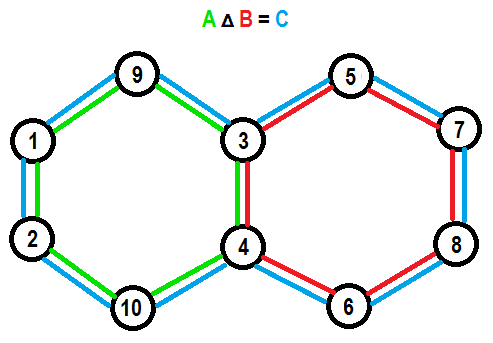
Another important property of circuits, symmetric difference of two different circuits always contain a circuit. Symmetric difference of two sets contains all elements that are included only in one of the sets (formally, $A \Delta B = (A \setminus B) \cup (B \setminus A)$). This property is related to cycle spaces, in case of matroids this can be generalized to “circuit spaces”.↵
↵
**Ranks. Ranking function.** Rank of matroid is size of its bases. But we can directly refer it as size of the basis, why would we need specific definition for such thing? Yes, this is not really a flexible thing (we can refer it as size of basis), to make it more flexible we can define ranking function $r(S)$ that tells maximum size of independent subset for some $S$, which is subset of ground set. Value of ranking function on some subset can be referred as rank of this subset in matroid. This information about subsets can be very helpful in many situations. Some properties of ranking functions: ↵
↵
1. Rank of subset cannot be greater than size of this subset.↵
2. Rank of independent subset is size of this subset.↵
3. Rank of whole ground set is equal to rank of matroid. Rank of empty set is $0$.↵
4. Rank of any subset of set $S$ is not greater than rank of $S$.↵
5. Including $1$ element into set can only increase its rank by $1$ or leave it unchanged. (formally, for some set $S$ and element $x \notin S$ we have $r(S) \leq r(S \cup \\{x\\}) \leq r(S)+1$)↵
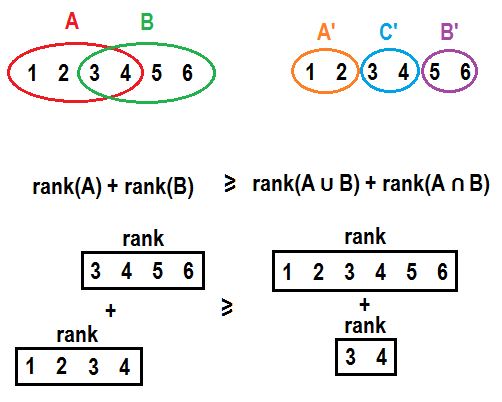
6. Ranking function of matroid is submodular. If we have two sets $A$ and $B$, moving all elements that are present in $B$ but not present in $A$ from $B$ to $A$ will not improve sum of ranks of both sets. Formally, $r(A) + r(B) \geq r(A \cup B) + r(A \cap B)$. In general element will not contribute more to a rank if it is moved to a set with additional elements. This might get more clear if explicitly split $A$ and $B$ into $A’ = A \setminus B$, $C’ = A \cap B$ and $B’ = B \setminus A$ and write it in a form $r(A’ \cup C’) + r(B’ \cup C’) \geq r(A’ \cup B’ \cup C’) + r(C’)$. See pictures below for example:↵
↵
↵
↵
Speaking informally, principle “it is better not to puts many eggs into one basket” works here.↵
↵
**Independence oracle.** Speaking about classifications of subsets, we usually cannot afford storing it as some information about each subset (it will result in exponential memory consumption). We need some other tools to test subsets for independence. If matroid is defined as a consequence of relations among elements in some other structure, we usually (probably, always?) can find algorithm with polynomial running time to test some subset of elements for independence. As we would like to abstract concept of matroids and use them regardless of their underlying independence mechanism, we can define _independence oracle_ as subroutine that tests some subset for independence. And we can measure running time of some algorithms as the number of _oracle calls_. (However, in practice we cannot completely forget about this, because we will miss great opportunities to optimize related algorithms.)↵
↵
#### Examples↵
↵
There are matroids of different types. There are some examples:↵
↵
**Uniform matroid.** Matroid that considers subset $S$ independent if size of $S$ is not greater than some constant $k$ ($|S| \leq k$). Simplest one, this matroid does not really distinguish elements of ground set in any form, it only cares about number of taken elements. All subsets of size $k$ are bases for this matroid, all subsets of size $(k+1)$ are circuits for this matroid. We can also define some specific cases of uniform matroid: ↵
↵
1. Trivial matroid. $k = 0$. Only empty set is considered independent, any element of ground set is considered dependent (any combination of ground set elements is also considered dependent as a consequence).↵
2. Complete matroid. $k = |X|$. All subsets are considered independent including complete ground set itself.↵
↵
**Linear (algebra) matroid.** Ground set consists of vectors of some vector space. Set of vectors is considered independent if it is linearly independent (no vector can be expressed as linear combination of other vectors from that set). This is the matroid from which whole matroid theory originates from. Linear bases of vector set are bases of matroid. Any circuit of this matroid is set of vectors, where each vector can be expressed as combination of all other vectors, but this combination involves all other vectors in circuit. Independence oracle for this matroid can be based on gaussian elimination.↵
↵
**Colorful matroid.** Ground set consists of colored elements. Each element has exactly one color. Set of elements is independent if no pair of included elements share a color. Rank of a set is amount of different colors included into a set. Bases of this matroid are sets that have exactly one element of each color. Circuits of this matroid are all possible pairs of elements of the same color. Colors can be enumerated with integers for practical purposes.↵
↵
**Graphic matroid.** This matroid is defined on edges of some undirected graph. Set of edges is independent if it does not contain a cycle. This type of matroids is the greatest one to show some visual examples, because it can include dependent subsets of a large size and can be represented on a picture at the same time. If graph is connected then any basis of this graph is just a spanning tree of this graph. If graph is not connected then basis is a forest of spanning trees that include one spanning tree for each connected component. Circuits are simple loops of this graph. Independence oracle for this matroid type can be implemented with DFS, BFS (start from each vertex in graph and check that no edge connect a vertex with already visited one) or DSU (keep connected components, start with disjoint vertices, join by all edges and ensure that each edge connected different components upon addition). Here is an example of circuit combinations property in graphic matroid:↵
↵
↵
↵
**Truncated matroid.** We can limit rank of any matroid by some number $k$ without breaking matroid properties. For example, base of truncated colorful matroid is set of elements that include no more than $k$ different colors and all colors are unique. Base of truncated graphic matroid is acyclic set of edges that leaves at least $(n-k)$ connected components in the graph (where $n$ is amount if vertices in a graph). This is possible because third matroid property does not only refer to bases of matroid, but to any independent set in matroid, and when all independent sets with sizes greater than $k$ are simultaneously removed, independent sets of size $k$ become new bases and for any lesser independent set can still find elements from each basis that can be added.↵
↵
**Matroid on a subset of ground set.** We can limit ground set of matroid to its subset without breaking matroid properties. This is possible because rules of dependence does not rely on specific elements being in ground set. If we remove an edge from a graph, we will still have a valid graph. If we remove an element from set (of vectors or colored elements) we will still get a valid set of some element of the same type, and rules will preserve. Now, we can also define rank of subset in matroid as a rank of matroid on a ground set limited to this subset.↵
↵
**Expanded matroid. Direct matroid sum.** We can consider two matroids as one big matroid without any difficulties if elements of ground set of first matroid does not affect independence, neither intersect with elements of ground set of second matroid and vise versa. Think of two graphic matroids on two connected graphs. We can unite their graphs together resulting in graph with two connected components, but it is clear that including some edges in one component have no effect on other component. This is called _direct matroid sum_. Formally, $M_1 = \left\langle X_1, I_1 \right\rangle, M_2 = \left\langle X_2, I_2 \right\rangle, M_1 + M_2 = \left\langle X_1 \cup X_2, I_1 \times I_2 \right\rangle$, where $\times$ means cartesian product of two sets. You can unite as many matroids of as many different types without restrictions as you want (if you can find some use for the result).↵
↵
_This is not the only types of matroids. You can find more information about useful matroid types or even create your own._↵
↵
#### Rado-Edmonds algorithm↵
↵
Now, speaking about practical purposes of matroids. We have the following problem: we need to find a basis in matroid $M = \left\langle X, I \right\rangle$. How do we approach this problem efficiently?↵
↵
According to third matroid property, if we have some independent set $S$ which size is less than size of a basis we can find some element $x$ that can be added to $S$ without loss of independence. So, we can start with empty set that is guaranteed to be independent and add elements one-by-one performing a linear scan over ground set to find next element to add. If we denote $n$ as a size of ground set $X$ and $r$ as a rank of $M$ we have algorithm that runs in $\mathcal{O}(r \cdot n)$ _oracle calls_.↵
↵
But we can do it better, notice that if some element $x$ wasn’t added into $S$ on some step it will never be possible to include it on any future step, because if $S \cup \\{x\\}$ was considered dependent on some step it includes some circuit $C$ and we never exclude elements in this algorithm, so any future expanded version of $S$ will also confirm $S \cup \\{x\\}$ to include some circuit $C$ and be dependent. So we can find a basis in one single scan, if we will take elements greedily (include element into $S$ if it does not break independence of $S$ at the step). So, we have improved runtime to $\mathcal{O}(n)$ _oracle calls_.↵
↵
But, what about weighted case? Let each element $x$ of the ground set have some weight $w(x)$. We want to find a basis in our matroid with minimal sum of weights.↵
↵
_You probably know about Kruskal’s minimum spanning tree algorithm, which actually solves the problem for graphic matroid, but how do you prove it without recalling some of matroid properties?_↵
↵
Keeping in mind greedy ideas, we can try to connect results of $k$-th and $(k+1)$-th steps of algorithm to show something. Let’s assume that $A$ is the minimum weight independent set of size $k$ and $B$ is minimum weight independent set of size $(k+1)$. By third matroid property, we have at least one element $y$ in $B$ that can be added into $A$ without loss of independency. So, we have sets $B \setminus \\{y\\}$ of size $k$ and $A \cup \\{y\\}$ of size $(k+1)$. As we know what are minimum weighted sets, we can write down:↵
↵
$A \leq B \setminus \\{y\\}$↵
↵
$B \leq A \cup \\{y\\}$↵
↵
we add $y$ to both sets in first inequality and get:↵
↵
$A \cup \\{y\\} \leq (B \setminus \\{y\\}) \cup \\{y\\}$↵
↵
$A \cup \\{y\\} \leq B$↵
↵
we can see that↵
↵
$B \leq A \cup \\{y\\} \leq B$↵
↵
which means↵
↵
$B = A \cup \\{y\\}$↵
↵
In other words, we can get minimum weight independent set of size $(k+1)$ from minimum weight independent set of size $k$ by including some element $y$ into it which will not break independence. What if we have multiple of such elements $y$? Greedy answer, $y$ with minimum weight.↵
↵
Combining this with previous result we can present algorithm that will find basis with minimum sum of weights:↵
↵
1. Sort elements of ground set by ascending weight↵
2. Start with empty set $S$↵
3. Iterate elements of ground set in sorted order, at each step include current element into $S$ if it does not make $S$ dependent ↵
↵
Running time is $\mathcal{O}(n \cdot log(n))$ unit operations for sort plus $\mathcal{O}(n)$ _oracle calls_.↵
↵
This is Rado-Edmonds algorithm. As an example for specific matroid type we have Kruskal’s minimum spanning tree algorithm, mentioned above.↵
↵
If finding a basis of any matroid is done greedily and matroids are about generalizing things, probably we can prove that all greedy problems can be reduced to finding a base of some matroid? Well, no. ↵
↵
In greedy solutions we can sometimes not only sort elements, but also create additional elements in process or use some specific comparators or skip / take conditions. Even if we forget about weights and put some additional constraints, we can only use matroids in some specific cases. In general, if you want to prove that matroids are applicable here, you can focus on proving axiomatic properties.↵
↵
Matroid intersection↵
------------------↵
↵
And you may ask “Why would we ever need all these generalizations, if it does not invent anything new, anything that is not covered with other more situational and problem-specific algorithms?” Well, there are some problems that are extremely hard (in my opinion) to solve without using these generalizations. One of these problems is the problem of matroid intersection.↵
↵
More detailed, this problem should be called “finding largest common independent set in intersection of two matroids”. Formally, we are given two matroids $M_1 = \left\langle X, I_1 \right\rangle$ and $M_2 = \left\langle X, I_2 \right\rangle$ and we want to find any set $S$ with $\max\limits_{S \in I_1 \cap I_2} |S|$. In other words largest possible $S$ that is considered independent by both matroids.↵
↵
We can show multiple examples of such problems. I mostly like these: ↵
↵
**Colorful spanning tree.** You are given a graph and a color for each edge in that graph. You have to find spanning tree of this graph that has no more than one edge of each color. Clearly, matroid classifications are “set of edges contains no more than two edges of a same color” and “set of edges contains no cycles”.↵
↵
**Colorful linear basis.** You are given a set of vectors in some vector space and a color for each given vector. You have to find a basis of given set of vectors that includes no more than one vector of each color. Here we go with linear independence on one and unique colors on the other.↵
↵
**Bipartite graph maximum matching.** Well known problem, you are given bipartite graph find subset of edges of maximum size such that no pair of edges from this subset share a vertex. Might not be obvious, what should we do here, but think of easier version of the problem: replace “no pair share a vertex” with ”no pair share a vertex from the left part”. Now we can easily solve that problem with picking one edge for each vertex on a left part with non-zero power, also we can show that it can be done greedily and it forms a proper matroid. And as we have two parts in given graph, we can obtain second matroid for the right part symmetrically and solve intersection problem.↵
↵
Wait, but why exactly two matroids? What about intersecting more? Well, that significantly expands the number of problems that can be reduced to intersection of multiple matroids. In fact this stuff becomes general enough to offer a solution for Hamiltonian path problem. Given directed graph, intersect these three matroids on ground set of edges of a graph:↵
↵
1. Ensure each vertex has at most $1$ outcoming power (can be represented as colorful matroid, paint edges that come out of the same vertex into one color)↵
2. Ensure each vertex has at most $1$ incoming power (just as previous one)↵
3. Ensure there is no loops (forget about edges direction and check that edges form a forest of spanning trees)↵
↵
And… it is NP-complete. Which means we have no idea how to solve it in polynomial time.↵
↵
So, returning to two matroids. How can we approach this problems? Bruteforce exponential solution is pretty obvious (check all the sets from either $I_1$ or $I_2$). Difficulties start from the point that $\left\langle X, I_1 \cap I_2 \right\rangle$ is not guaranteed to form a proper matroid. As we know finding a basis of any matroid can be done greedily and, well, randomly picking edges into a matching is not a great way to solve it. ↵
↵
_Probably, you know about Kuhn’s bipartite matching algorithm and using the fact that these problems are similar you may somehow come to a general solution._↵
↵
We need some observations here. Consider single matroid $M = \left\langle X, I \right\rangle$ and some basis $B$ in it (and this basis is not unique, otherwise that would be a trivial case). We can always find some element $p$ that can be excluded from $B$ and some other element $q$ can be included in $B$ instead, so that it will not break independence (formally, $B \setminus \\{p\\} \cup \\{q\\} \in I$). ↵
↵
For example, considering $M$ is graphic matroid of the following graph, red and yellow edges form a spanning tree, which is a basis of $M$. ↵
↵
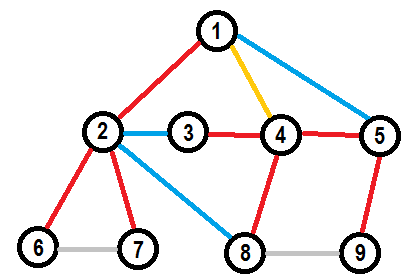↵
↵
We can exchange yellow edge for one of blue edges to get one-edge-different spanning tree. Let’s call this _exchange_ operation. Let’s see if we can find a sequence of exchange operations that will change our basis $B$ to some other valid basis of matroid $M$. ↵
↵
For example, there are two different spanning trees of the same graph:↵
↵
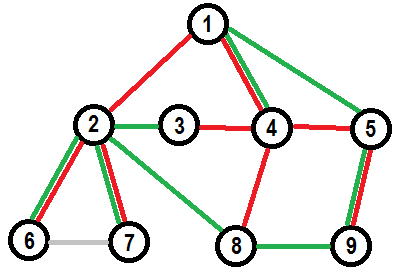↵
↵
We can get green tree from red tree with this sequence of exchanges:↵
↵
1. Exchange $(4,5)$ to $(1,5)$↵
2. Exchange $(4,8)$ to $(8,9)$↵
3. Exchange $(1,2)$ to $(2,3)$↵
4. Exchange $(3,4)$ to $(2,8)$↵
↵
Note, that swapped pairs and sequence of operations if important. We cannot exchange $(3,4)$ to $(2,8)$ earlier than $(1,2)$ to $(2,3)$ as it will result in leaving vertex $3$ isolated and creating a cycle in other part of a graph. Also, we cannot start with swapping $(4, 5)$ to $(2, 8)$.↵
↵
<spoiler summary="General algorithm for finding such sequence for graphic matroid">↵
↵
We have connected graph $G$ with $n$ vertices and two spanning trees of $G$, let’s call them white tree and black tree. We need to find some sequence of exchanges, than will one-by-one replace all white edges with all black edges, maintaining valid spanning tree after each operation.↵
↵
Notice that we have two equal criterias for forming a spanning tree from a set of $(n-1)$ edges:↵
↵
1. There is no cycles in it↵
2. All $n$ vertices are forming a single connected component with these edges↵
↵
So, we can focus only on one of them. We can check forming a single connected component.↵
↵
Root white spanning tree in some vertex $r$. Now there is at least one leaf (vertex that does not have any children) in white rooted tree. Consider any leaf $l$, it is connected by exactly one white edge with it’s parent and at least one black edge with some other vertex in $G$. Exchange this white edge to any black edge $(l, p)$ connected with this leaf. Now, we can see that our leaf will always be connected with $p$ for all the future operations (we do not want to cancel addition of black edge). As we care only about connectivity, compress $l$ and $p$ together. Now we have eliminated one vertex of a graph and one white edge and we now have a tree of $(n-1)$ vertices and $(n-2)$ white edges to exchange. ↵
↵
Again, we can find and eliminate one leaf with an edge to it as described above. We can continue doing it until we have single vertex left and all white edges are exchanged.↵
↵
</spoiler>↵
↵
It appears that we can _always_ find a sequence of exchange operations that will change our basis $B$ to _any_ other valid basis of matroid $M$ regardless of its type. This property is called “strong basis exchange” lemma and can be strictly proven in general form. We can generalize strong basis exchange to exchange of any independent sets of equal size, using the fact that they are valid bases of truncated version of matroid $M$.↵
↵
Knowing this, we want to find a good representation for all possible exchanges of ground set elements for some independent set $S$. Possible exchange is a relation between two elements: $x$ in $S$ and $y$ not in $S$. Well known fact, graphs are great way to represent relations between pairs of elements. We can define a structure called _exchange graph_ $D_M (S)$ of independent set $S$ in matroid $M$ as bipartite graph which contains edge $(x, y)$ if we can exchange $x$ to $y$ in $S$ without loss of independency (formally, $D_M (S)$ contains edge $(x, y)$ if $x \in S, y \in X \setminus S, S \setminus \\{x\\} \cup \\{y\\} \in I$). ↵
↵
For future I will refer part that contains elements in $S$ as “left” part and part that contains elements not in $S$ as “right” (that will be consistent with pictures).↵
↵
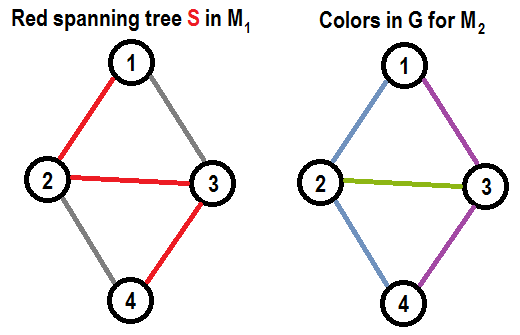
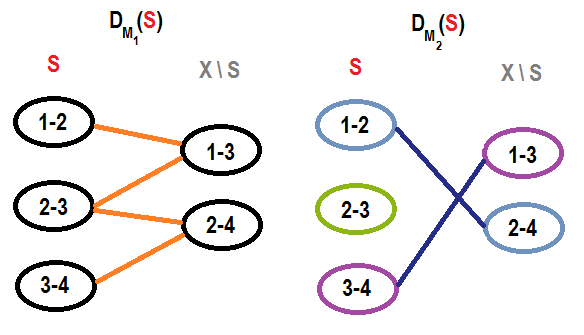
For example, there is some small graph $G$, red spanning tree $S$ and it’s exchange graph $D_M (S)$ on a graphic matroid $M$ of $G$:↵
↵
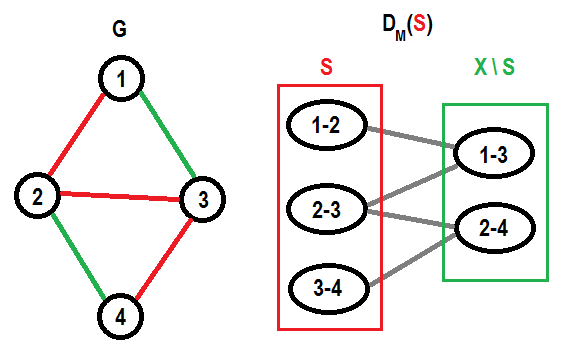↵
↵
What does exchange graph offer to us? As first, consider some other independent set $T$ with equal size ($|S| = |T|$). There exists a perfect matching in $D_M (S)$ between $S \setminus T$ and $T \setminus S$ (between elements that are included in one set, but not included in other and their symmetry). By generalization of strong basis exchange we can swap elements one-by-one forming this perfect matching one edge per step.↵
↵
However, the opposite does not hold. We cannot guarantee that we can choose any matching in exchange graph, perform changes associated with selected edges and get independent set. Showing this for colorful matroid is trivial, we can change any element to element of unused color $c$, but we cannot change any two elements (not of color $c$) to two elements of color $c$ simultaneously. For graphic matroid consider the following acyclic red set of edges in given graph:↵
↵
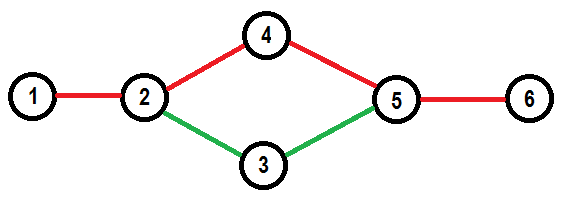↵
↵
We can exchange $(1, 2)$ to $(2, 3)$, symmetrically we can exchange $(5, 6)$ to $(3, 5)$. However we cannot perform these changes simultaneously.↵
↵
So, how can we understand whether changes can break things or they will preserve independence? We can notice that there are multiple ways to shuffle in some circuit $C$ into our independent set $S$ following exchange edges in $D_M (S)$. In example above we can also obtain the same circuit $(2-3-5-4)$ exchanging $(5, 6)$ to $(2, 3)$ and $(1, 2)$ to $(3, 5)$. Is it always the case? ↵
↵
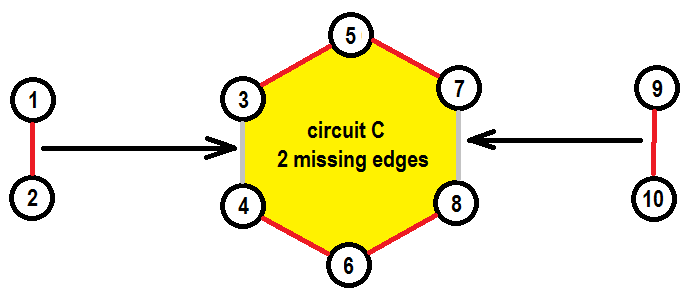
Let’s try to construct a case when there is only one way to get a dependent set by following edges in $D_M (S)$. So, we are looking for some circuit $C$ to be formed in result of exchanges. We are not interested in exchange edges connecting two elements of $C$ as picking any of them into matching will immediately break circuit $C$ (there is no way to insert removed element back). This $C$ must have at least $2$ “vacant” places for elements to exchange into (at least two elements of $C$ must not be in $C$, $|C \setminus S| \geq 2$).If there is only “vacant” place there will be no edge in exchange graph to this element from any element that does not belong to $C$, because including this element will result in immediate completion of circuit $C$ and loss of dependency, this is not allowed by construction of exchange graph. So, we are generally looking for some structure of this form:↵
↵
↵
↵
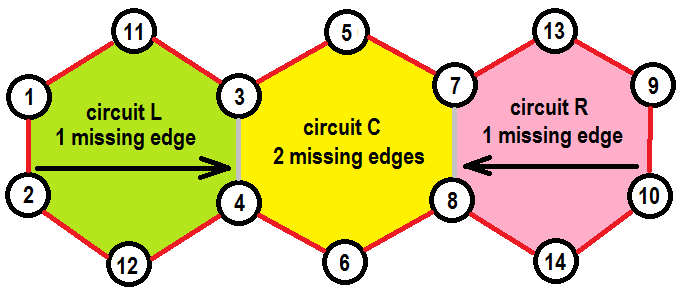
Here, edges of independent set $S$ are marked red, edges not included in $S$ are marked gray, planned edge exchanges are marked with black arrows. Circuit $C$ contains all edges that form the border of yellow area ($C$ is $(3-5-7-8-6-4)$). Now, there are two ways to exchange edges to complete $C$. We want to find a way to restrict exchanging $(9, 10)$ to $(3, 4)$ and $(1, 2)$ to $(7, 8)$. The only way of doing this in terms of exchange graph is to construct additional circuit $L$ around $(3, 4)$ that would include edge $(1, 2)$ and not include $(9, 10)$ and put all edges from $L$ into $S$ except $(3, 4)$. This way exchanging $(9, 10)$ to $(3, 4)$ will lead to completing $L$, but exchanging $(1, 2)$ to $(3, 4)$ will still be possible. Symmetrically, we can construct circuit $R$ around $(7, 8)$.↵
↵
↵
↵
That’s it? Huh, something actually went wrong, as these actions led us to including a great circuit formed by all red edges into $S$. But $S$ must be independent. That happened because in terms of linear combinations some element $x$ plays the same role as some circuit $L$ that includes element $x$ without given element $x$ ($L \setminus \\{x\\}$). That is why it is actually called a circuit. Note, that vertices $3$ and $4$ can be connected with direct edge $(3,4)$, but also with remaining part of circuit $L$ which is $(3-11-1-2-12-4)$. Increasing the number of elements in $C$ not included in $S$ will not help, because we will still need a circuit connecting endpoints for each missing edge. Changing the type of matroid will not help either, properties of linear combinations will preserve.↵
↵
So, there is no way to restrict number of ways to include circuit $C$ to $1$ by edges of exchange graph. This means that there are _always_ at least $2$ ways to include any circuit into our set using exchange graph. That also means if there is only one way to get some other set $T$ from $S$ using $D_M (S)$, it is guaranteed for $T$ to be independent. In other words, we can say that $T$ will be independent if matching between $S \setminus T$ and $T \setminus S$ in $D_M (S)$ is _unique_.↵
↵
_All articles that I’ve seen prove this fact in other way that seems less obvious for me, but that may not be the case for you._↵
↵
Now that’s clear how we can reliably obtain some other independent sets of equal size. But remember that we need to do this for two matroids at the same time and also would like to somehow obtain the maximum size independent set, not just equal all the time.↵
↵
Considering two matroids $M_1 = \left\langle X, I_1 \right\rangle$ and $M_2 = \left\langle X, I_2 \right\rangle$ and some set $S$ independent for both ($S \in I_1 \cap I_2$), we can see that exchange graphs $D_{M_1} (S)$ and $D_{M_2} (S)$ have same vertices and bipartition. That’s good, these graphs only differ in set of edges, so we can meld them together resulting in a single graph with edges of two types. Let’s call this graph $D_{(M_1, M_2)} (S)$. Now we can say that some set $T$ is also independent for both matroids if there exists a perfect matching between $S \setminus T$ and $T \setminus S$ for both types of edges in $D_{(M_1, M_2)} (S)$. ↵
↵
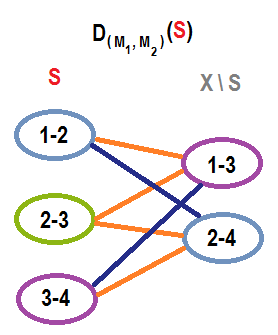
For example, consider a problem of colorful spanning tree on this small colorful graph $G$ and multiple exchange graphs built for colorful spanning tree $S$ (marked with red). $M_1$ refers to graphic matroid, $M_2$ refers to colorful matroid.↵
↵
↵
↵
↵
↵
↵
↵
There are only two colorful spanning trees of this graph ($S = \\{(1, 2), (2, 3), (3, 4)\\}$ and $T = \\{(1, 3), (2, 3), (2, 4)\\}$) and there exist a perfect matching between $S \setminus T = \\{(1, 2), (3,4)\\}$ and $T \setminus S = \\{(1, 3), (2, 4)\\}$ in both types of edges of $D_{(M_1, M_2)} (S)$.↵
↵
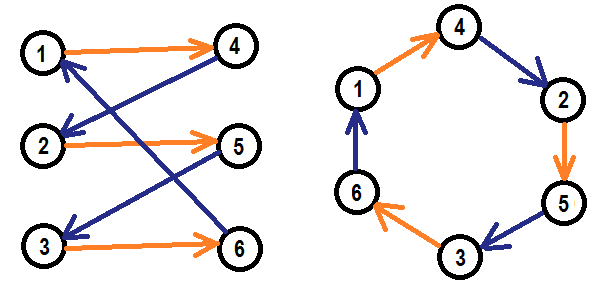
There is a cool way to generate a perfect matching within two sets of edges in bipartite graph between two sets of edges in different parts. Orient one type of edges from left part to right, and second type of edges from right part to left, and find a cycle containing all required vertices. Take a look at the example:↵
↵
↵
↵
Each vertex in a loop touches exactly one odd and one even edge. Edges in a loop will have their types according to their parity. This loop will always have odd length, so decomposition into two perfect matchings in edges of different types is obvious.↵
↵
Now we need to think about increasing the size of our independent set $S$. In a single matroid if independent set $S$ is not a basis we can always find at least one element that can be added into $S$ without loss of independence (by the third axiomatic property of matroids). Now, let’s group all elements that can be added into $S$ keeping it independent in $M_1$ into set $Y_1$ (formally, $x \in Y_1$ if $x \notin S, S \cup \\{x\\} \in I_1$).The same for $Y_2$ in $M_2$.↵
↵
Let’s see what can we do with this information. Firstly, if there is an element $x$ that belongs to both $Y_1$ and $Y_2$, that’s the jackpot, perfect option to include in $S$ immediately! Secondly, if $Y_1$ is empty or $Y_2$ is empty we can conclude that we have reached the basis in one of matroids and no future growth available for $S$. ↵
↵
But what should we do in general case? Let’s orient edges in $D_{(M_1, M_2)} (S)$. Edges from $D_{M_1} (S)$ from left to right, edges from $D_{M_2} (S)$ from right to left and find a… cycle? No. A path from any vertex in $Y_1$ to any vertex in $Y_2$. This will serve us two purposes at the same time. But why and how is this supposed to work?↵
↵
Firstly, selecting a path without shortcuts guarantees us uniqueness of perfect matchings along the path. Until there is a shortcut for some path, let’s use it and then we will eventually end up with path, where the $i$-th vertex in that path is connected only with $(i+1)$-th and probably with any subset of previous vertices, but it is not considered to be a shortcut because graph is oriented. Let’s call path from any vertex in $Y_1$ to any vertex in $Y_2$ without shortcuts to be _augmenting path_. But members of $Y_1$ and $Y_2$ are both in a right part, so the path will have odd length, matching will not include all vertices from the right part. Well, yes, but it will include all vertices from the left part, and will not include one vertex from the right part. For edges of $D_{M_1} (S)$ matching will not include first vertex of augmenting path, for edges of $D_{M_2} (S)$ last vertex of the path will not be included.↵
↵
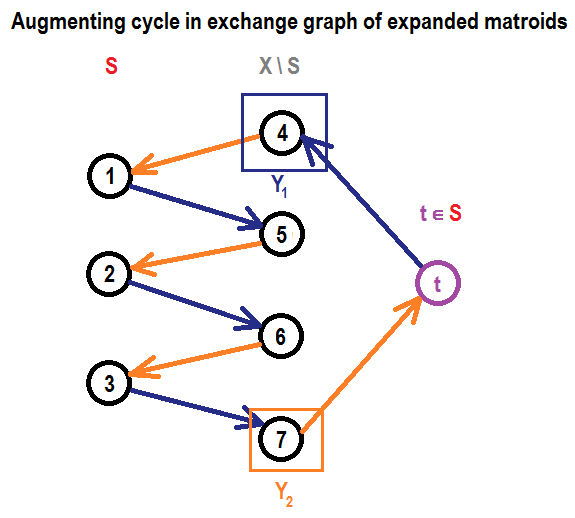
And here second purpose comes in play, which is increasing size of $S$. Let’s expand ground set of both matroids with one temporary vertex $t$ which is completely independent from all other elements for both matroids and include it into $S$. There will be an edge between $t$ and members of $Y_1$ in $D_{M_1} (S)$ and between $t$ and members of $Y_2$ in $D_{M_2} (S)$. So we can complete our augmenting path to cycle, connecting last vertex to $t$ and $t$ to first vertex. So, the whole picture will look like this (for clarity, only edges included into cycle are shown)↵
↵
↵
↵
There will be unique matching in this cycle, as a consequence of uniqueness of matching in selected path, so we can perform a set of exchanges associated with selected edges (in fact selected vertices). We have included a temporary vertex $t$, that will be removed from $S$ after performing selected exchanges. So we get an independent set $S$ on expanded matroids but without usage of $t$, which means we can forget about $t$ and say that we increased size of $S$ by $1$ performing these operations on original matroids.↵
↵
Now we established the way of increasing size of $S$ by one. So we can start with empty $S$ and go ahead until we are able to find valid augmenting path.↵
↵
Fine, but what about sufficiency? How can we show that we will not fail to augment our independent set earlier than reaching its maximum size? If either $Y_1$ or $Y_2$ is empty, that means we have reached basis in one of matroids and this is clearly the maximum for intersection (due to third axiomatic matroid property we can always find an element that can be added to independent set if it is smaller than basis).↵
↵
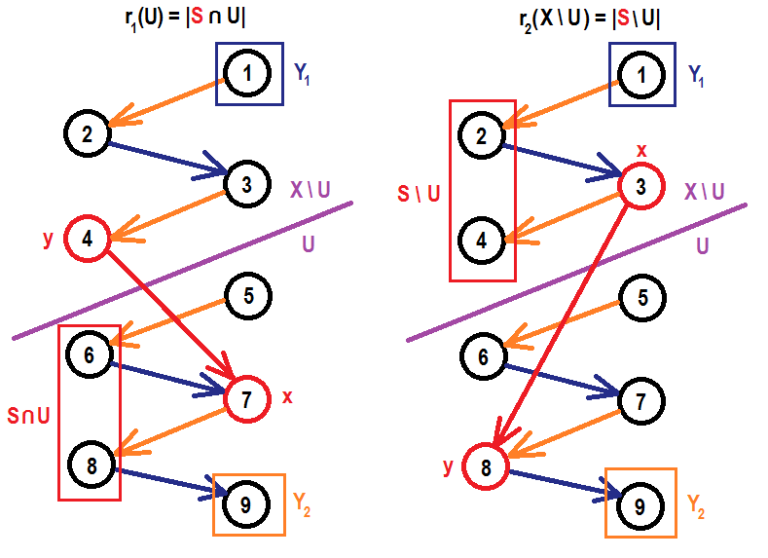
What about the case, when we haven’t reached any of bases, but fail to find augmenting path? We need some theory here. Consider some set $S$ that is independent for both matroids $M_1$ and $M_2$ with rank functions $r_1$ and $r_2$, respectively. Now split ground set $X$ into two parts $U$ and $X \setminus U$. Elements of $S$ that were split into the same part must be independent for both matroids, speaking in terms of ranking functions we can write down $4$ inequalities:↵
↵
1. $|S \cap U| \leq r_1(U)$↵
2. $|S \cap U| \leq r_2(U)$↵
3. $|S \cap (X \setminus U)| \leq r_1(X \setminus U)$↵
4. $|S \cap (X \setminus U)| \leq r_2(X \setminus U)$↵
↵
combining $1$ and $4$ we can get↵
↵
$|S \cap U| + |S \cap (X \setminus U)| \leq r_1(U) + r_2(X \setminus U)$↵
↵
$|S| \leq r_1(U) + r_2(X \setminus U)$↵
↵
considering all possible splits (all possible $U$) and independent set $S$ of maximum size we get↵
↵
$\max\limits_{S \in I_1 \cap I_2} |S| \leq \min\limits_{U \subseteq X} (r_1(U) + r_2(X \setminus U))$↵
↵
Seems complicated enough, but we are entering all these difficulties to show reaching limit. If we can show equality that will confirm that we have reached this limit and cannot get any better result. So, we want to prove:↵
↵
$\max\limits_{S \in I_1 \cap I_2} |S| = \min\limits_{U \subseteq X} (r_1(U) + r_2(X \setminus U))$↵
↵
This theoretical limit is known as Edmonds-Lawler theorem or matroid intersection min-max relation. ↵
↵
Note, that with equality we do not care about minimum in the right part, it is enough for us for find any partition $U$ that will satisfy equality (in fact, that will be the minimum because right part cannot be less than left). We want to analyze the case, when we have no path from $Y_1$ to $Y_2$, so we can consider a split that is based on reachability of $Y_2$. Let vertex $x$ be included in $U$ if there is a path from $x$ to some vertex in $Y_2$. Now, we can split equality back↵
↵
$|S| = |S \cap U| + |S \setminus U| = r_1(U) + r_2(X \setminus U)$↵
↵
into↵
↵
$|S \cap U| = r_1(U)$↵
$|S \setminus U| = r_2(X \setminus U)$↵
↵
Suppose $r_1(U) > |S \cap U|$, that would mean that there exists another independent set $T$ in $U$ which is larger than $S \cap U$. By matroids property, there exists some element $x$ in $T$ that can be added into $S \cap U$ without loss of independence in $M_1$, generalizing $U$ to $X$ we cannot guarantee that $S \cup \\{x\\}$ will be independent in $M_1$, but it will include at most one circuit $C$ that will have some element $y$ not from $U$ (otherwise we cannot satisfy existence of greater independent set $T$ in $U$). If there is no circuit $C$ then any element $y$ not from $U$ can be exchanged to add $x$. But that means that there exists directed edge $(y, x)$ in exchange graph $D_{(M_1, M_2)} (S)$, that would mean that we can reach $Y_2$ from $y$ through that edge and vertex $x$, but we made an assumption that $y$ is not in $U$, so there is no path from $y$ to $Y_2$. We got a contradiction, so that proves $r_1(U) = |S \cap U|$.↵
↵
Symmetrically, we can prove that $r_2(X \setminus U) = |S \setminus U|$. ↵
↵
These contradictions are visualized on pictures of exchange graph below. Set $U$ splits ground set $X$ into two parts (below and above purple line), vertex in $Y_2$ can be reached from each vertex below the line and cannot be reached from any vertex above the line. In other words there is no edge that comes from upper part and goes to lower part crossing purple line, which shows that red edge cannot exist.↵
↵
↵
↵
Proving both equalities, we prove Edmonds-Lawler theorem and prove that we always reach optimal solution with this algorithm.↵
↵
Matroid intersection problem can be generalized to weighted case. Also there are a lot of interesting related stuff that is worth mentioning, but this theoretical part is already vast and I do not want to make it even larger. Check resources from “Useful links” chapter for more.↵
↵
Implementation and complexity, oracles↵
------------------↵
↵
Now, we have all the theory we need to actually implement a solution for matroid intersection problem.↵
↵
Remember, we are given two matroids $M_1 = \left\langle X, I_1 \right\rangle$ and $M_2 = \left\langle X, I_2 \right\rangle$ with ranking functions $r_1$ and $r_2$ respectively and independence oracles with running times $C_1$ and $C_2$ respectively. We need to find largest set $S$ that is independent for both matroids.↵
↵
According to algorithm we need to start with empty $S$ and then repeat the following until we fail to do this:↵
↵
1. Build exchange graph $D_{(M_1, M_2)} (S)$↵
2. Find “free to include vertices” sets $Y_1$ and $Y_2$↵
3. Find augmenting path without shortcuts $P$ from any element in $Y_1$ to any element in $Y_2$↵
4. Alternate inclusion into $S$ of all elements in $P$↵
↵
Let $r$ be the size of the result, $r = |S|$. Let $n$ be the size of ground set, $n = |X|$. We can safely assume that $r \leq min(r_1(X), r_2(X))$ because common independent set cannot be larger than size of bases in both intersecting matroids. So, main loop (augmentation process) will be repeated $r$ times.↵
↵
On each iteration we have $4$ steps:↵
↵
1. Building exchange graph is actually checking presence of all edges in bipartite graph with partition $S$ and $X \setminus S$. We measure their sizes as $|S| = \mathcal{O}(r)$ and $|X \setminus S| = \mathcal{O}(n)$. Between each pair of vertices from different parts there are two edges possible (one is from left to right, other is from right to left). Checking their presence requires $1$ oracle call for both matroids. So checking presence all edges, will be $\mathcal{O}(r) \cdot \mathcal{O}(n) \cdot (C_1 + C_2) = \mathcal{O}(r \cdot n \cdot (C_1 \cdot C_2))$.↵
2. Building $Y_1$ requires $1$ first oracle call for each vertex from right part $X \setminus S$, that gives runtime $\mathcal{O}(n \cdot C_1)$. Symmetrically, building $Y_2$ requires $1$ first oracle call for each vertex from right part $X \setminus S$, that gives runtime $\mathcal{O}(n \cdot C_2)$. Combining we get $\mathcal{O}(n \cdot (C_1 + C_2)).$↵
3. Hm, finding “a path without shortcuts”. Shortest path will do the trick. So, here we go with breadth-first search. Runtime is $\mathcal{O}(V + E) = \mathcal{O}(n + r \cdot n) = \mathcal{O}(r \cdot n).$↵
4. That’s the fastest one. Size of the shortest path cannot be greater than number of vertices in the graph. So, runtime is $\mathcal{O}(n)$.↵
↵
Without any cross-steps optimizations we have total running time $\mathcal{O}(r^2 \cdot n \cdot (C_1 + C_2))$. That is already good enough for some problems, but we can definitely go further this result.↵
↵
We can easily see that bottleneck for this algorithm is step $1$. Also we can see that this step does not require checking independence in arbitrary sets. We only need to take some independent set $S$ and exchange one pair of elements at a time. In general we need to remove at most 1 element and add at most 1 element and then check independence.↵
↵
We can find optimized matroid-type-specific solutions:↵
↵
**Colorful matroid.** We have elements of different colors, check whether we have more than $1$ element at the same time. Number of different colors cannot exceed $n$, we can use count array that will in $\mathcal{O}(1)$ tell us number of included elements of $i$-th color, add and remove elements. We generally do not need to do anything specific here, $\mathcal{O}(1)$ check is obvious combination of these operations.↵
↵
**Graphic matroid.** We have a forest of spanning trees, we need to check that exchanging edges does not include a loop. ↵
↵
We can $r$ times remove one edge and enumerate connected components and for each vertex find a connected component this vertex belongs to in $\mathcal{O}(n)$, and then we can add edge if and only if that edge connects different connected components. This requires $\mathcal{O}(r \cdot n)$ to prepare and allows checking presence of edge in $\mathcal{O}(1)$. Great balance between prepare and query parts, but generally it doesn’t allow doing anything more and seems to require $\mathcal{O}(r \cdot n)$ memory.↵
↵
We can try another approach. If added edge connects two different trees it will not break independence. If it connects two vertices in the same tree, then there is a loop, so we need to remove some other edge from that tree that belongs to this loop. So, if we add edge that connects $(x, y)$ we are fine only if we remove some other edge that belongs to a unique path in a tree between $x$ and $y$. We can reduce checking presence of edge in exchange graph to one query to check that some edge $(x, y)$ belongs to a path between some vertices $a$ and $b$. We can approach this problem with binary lifting, resulting in $\mathcal{O}(n \cdot log(n))$ precalc and $\mathcal{O}(log(n))$ per edge. Memory consumption can be reduced to $\mathcal{O}(n \cdot log(n))$.↵
↵
I haven’t tested which one is better. I think that the first way should perform better in practice unless memory limit is a problem.↵
↵
**Linear matroid.** We have a set of independent vectors in some vector space. We need to check whether we can remove one vector and add another. General approach is gaussian elimination, well known runtime is $\mathcal{O}(r^2 \cdot m)$, where $m$ is amount of dimensions of vector space. If vector space is $\mathbb{Z}_2^m$ we can apply bitset optimization achieving $\mathcal{O}(\frac{r^2 \cdot m}{w})$, where $w$ is size of machine word. But we can check loss of independency after addition of a single vector to a set faster if we have calculated basis of this set, we can do it in $\mathcal{O}(r \cdot m)$, because we only need to eliminate a single vector. We cannot find a way to remove a vector from a set after gaussian elimination was applied (I guess we can do something, but that won’t be easy and fast). But we can precalculate bases for each vector that can be removed and then eliminate a single vector instead of a whole set of vectors. Resulting runtime will be $\mathcal{O}(r^3 \cdot m)$ precalc and $\mathcal{O}(r \cdot m)$ per edge.↵
↵
But algorithm-specific oracles is not the only possible optimization here.↵
↵
We can notice that roles of matroids in exchange graph are not completely symmetrical. But it does not matter for solving the original problem. So, we can try swapping M_1 with M_2, and this may affect the runtime.↵
↵
To find a shortest path in a graph in general we don’t need to know the whole structure of a graph. If our oracles don’t take profits of building whole exchange graph at a time we can build it lazily, we can check presence of edges only when BFS tries to use them. We might think that it just improves the constant factor but article referenced in links under number $3$ contains this:↵
↵
_Cunningham has shown that we can find a maximum independent set with $\mathcal{O}(r^{1.5} \cdot n)$ oracle calls. The idea is to take a shortest augmenting path each time._↵
↵
Turns out this optimization actually improves complexity. In total we need $\mathcal{O}(\sqrt{r})$ times less oracle calls, when we construct exchange graphs lazily.↵
↵
Problem “Pick Your Own Nim“↵
------------------↵
↵
Sadly, I only know one problem that is directly involves algorithms that operate explicitly with matroids. I do not count applications of Rado-Edmonds algorithms and usage of matroid theory in proofs of correctness.↵
↵
_If you know some interesting problems about matroids, it would be great if you share them in comments._↵
↵
This problem is [problem:102156D] from [contest:102156].↵
↵
Shortly, problem gives us few boxes with numbers and asks us to choose exactly one number from each box in such way that we cannot choose non-empty subset of selected numbers with xor-sum equal to $0$. Or say that this is impossible. (Statement involves information about Nim game and Sprague-Grundy theorem but all the information we need to solve this problem is given in statement, and we do not need to care about it.) ↵
↵
Key observation here is that we cannot choose subset of numbers with zero xor-sum if and only if these numbers form independent set as vectors in $\mathbb{Z}_2^{60}$. Now reduction to matroid intersection comes obvious: ↵
↵
1. we want our set of numbers to be linearly independent, so we can use linear matroid↵
2. we want to choose exactly one number from each box. Colorful matroid can do the trick: assign the same color for all numbers in one box, different colors for different boxes.↵
↵
Now we can find largest independent set for both matroids and check that each color is used.↵
↵
So, this is the example of colorful linear basis problem. Involving some optimizations it can be solved in $\mathcal{O}(\frac{r^4 \cdot 60}{w} + \frac{r^{2.5} \cdot 60 \cdot n}{w})$. Assuming $\frac{60}{w}$ is $1$ or a small constant we can simplify it to $\mathcal{O}(r^4 + r^{2.5} \cdot n)$. Considering $r \leq 60, n \leq 5000$ it is about $10^7$ operations.↵
↵
<spoiler summary="Solution source code">↵
↵
~~~~~↵
#include <bits/stdc++.h>↵
↵
using namespace std;↵
↵
typedef long long int Z2Vector;↵
↵
struct GroundSetElement {↵
int color;↵
Z2Vector vector;↵
bool in_independent_set;↵
int independent_set_position;↵
int bfs_parent;↵
};↵
↵
struct Z2Basis {↵
vector<Z2Vector> vectors;↵
↵
void add_vector(Z2Vector new_vector) {↵
vectors.push_back(new_vector);↵
}↵
↵
void reset() {↵
vectors.clear();↵
}↵
↵
int size() {↵
return vectors.size();↵
}↵
↵
void gaussian_elimination() {↵
for (int i = 0; i < size(); i++) {↵
for (int j = i; j < size(); j++) {↵
if (vectors[i] < vectors[j]) swap(vectors[i], vectors[j]);↵
}↵
↵
for (int j = i+1; j < size(); j++) {↵
vectors[j] = min(vectors[j], vectors[j] ^ vectors[i]);↵
}↵
}↵
}↵
↵
bool independent_with(Z2Vector new_vector) {↵
for (auto v : vectors) new_vector = min(new_vector, new_vector ^ v);↵
↵
return new_vector > 0;↵
}↵
};↵
↵
int n;↵
int m;↵
↵
int color_count;↵
bool color_used[60+60];↵
↵
vector<GroundSetElement> ground_set;↵
vector<int> independent_set; /// as indexes of ground set↵
Z2Basis basis; /// of independent set↵
Z2Basis basis_without[60+60];↵
↵
bool linear_oracle(int inserted) {↵
return basis.independent_with(ground_set[inserted].vector);↵
}↵
↵
bool linear_oracle(int inserted, int removed) {↵
int wi = ground_set[removed].independent_set_position;↵
↵
return basis_without[wi].independent_with(ground_set[inserted].vector);↵
}↵
↵
void prepare_linear_oracle() {↵
basis.reset();↵
↵
for (int i = 0; i < independent_set.size(); i++) {↵
basis_without[i].reset();↵
}↵
↵
for (int i = 0; i < independent_set.size(); i++) {↵
basis.add_vector(ground_set[independent_set[i]].vector);↵
for (int j = 0; j < independent_set.size(); j++) {↵
if (i != j) basis_without[j].add_vector(ground_set[independent_set[i]].vector);↵
}↵
}↵
↵
basis.gaussian_elimination();↵
for (int i = 0; i < independent_set.size(); i++) {↵
basis_without[i].gaussian_elimination();↵
}↵
}↵
↵
bool colorful_oracle(int inserted) {↵
int inserted_color = ground_set[inserted].color;↵
↵
return !color_used[inserted_color];↵
}↵
↵
bool colorful_oracle(int inserted, int removed) {↵
int inserted_color = ground_set[inserted].color;↵
int removed_color = ground_set[removed].color;↵
↵
if (!color_used[inserted_color]) return true;↵
↵
return inserted_color == removed_color;↵
}↵
↵
void prepare_colorful_oracle() {↵
for (int c = 0; c < color_count; c++) {↵
color_used[c] = false;↵
}↵
↵
for (auto idx : independent_set) {↵
color_used[ground_set[idx].color] = true;↵
}↵
}↵
↵
bool augment() {↵
prepare_linear_oracle();↵
prepare_colorful_oracle();↵
↵
const int SOURCE = -1;↵
const int NOT_VISITED = -2;↵
const int NOT_FOUND = -3;↵
↵
for (int i = 0; i < ground_set.size(); i++) {↵
ground_set[i].bfs_parent = NOT_VISITED;↵
}↵
↵
int endpoint = NOT_FOUND;↵
↵
queue<int> q;↵
↵
for (int i = 0; i < ground_set.size(); i++) {↵
if (colorful_oracle(i)) {↵
ground_set[i].bfs_parent = SOURCE;↵
q.push(i);↵
}↵
}↵
↵
while (q.size()) {↵
int cur = q.front();↵
q.pop();↵
↵
if (ground_set[cur].in_independent_set) {↵
for (int to = 0; to < ground_set.size(); to++) {↵
if (ground_set[to].bfs_parent != NOT_VISITED) continue;↵
if (!colorful_oracle(cur, to)) continue;↵
↵
ground_set[to].bfs_parent = cur;↵
q.push(to);↵
}↵
} else {↵
if (linear_oracle(cur)) {↵
endpoint = cur;↵
break;↵
}↵
↵
for (auto to : independent_set) {↵
if (ground_set[to].bfs_parent != NOT_VISITED) continue;↵
if (!linear_oracle(cur, to)) continue;↵
↵
ground_set[to].bfs_parent = cur;↵
q.push(to);↵
}↵
}↵
}↵
↵
if (endpoint == NOT_FOUND) return false;↵
↵
do {↵
ground_set[endpoint].in_independent_set ^= true;↵
endpoint = ground_set[endpoint].bfs_parent;↵
} while (endpoint != SOURCE);↵
↵
independent_set.clear();↵
for (int i = 0; i < ground_set.size(); i++) {↵
if (ground_set[i].in_independent_set) {↵
ground_set[i].independent_set_position = independent_set.size();↵
independent_set.push_back(i);↵
}↵
}↵
↵
return true;↵
}↵
↵
void solve() {↵
cin >> n;↵
for (int i = 0; i < n; i++) {↵
ground_set.emplace_back();↵
ground_set.back().color = i;↵
ground_set.back().in_independent_set = false;↵
↵
cin >> ground_set.back().vector;↵
}↵
↵
cin >> m;↵
for (int i = 0; i < m; i++) {↵
int k;↵
cin >> k;↵
while (k--) {↵
ground_set.emplace_back();↵
ground_set.back().color = n+i;↵
ground_set.back().in_independent_set = false;↵
↵
cin >> ground_set.back().vector;↵
}↵
}↵
↵
color_count = n+m;↵
↵
while (augment()) ;↵
↵
if (independent_set.size() < color_count) {↵
cout << "-1\n";↵
return;↵
}↵
↵
for (int i = n; i < ground_set.size(); i++) {↵
if (ground_set[i].in_independent_set) cout << ground_set[i].vector << "\n";↵
}↵
}↵
↵
int main() {↵
solve();↵
}↵
~~~~~↵
↵
</spoiler>↵
↵
Useful links↵
------------------↵
↵
Surely, you can find all the information in google with queries like “matroid”, “matroid theory”, “matroid intersection” and “matroid intersection algorithm”. But I will list all important sources of information that helped me to learn matroids and prepare this article.↵
↵
1. [Wikipedia matroid page](https://en.wikipedia.org/wiki/Matroid). English version of this page contains a lot of information about the definitions, examples and related problems. ↵
2. [NEERC IFMO Wiki Matroids category](https://neerc.ifmo.ru/wiki/index.php?title=Категория:Матроиды) of about 20 useful articles. Some of them do not explain thing in details, including only most important points, but you can find some great images related to the topic here. _This seems to be only in russian._↵
3. [MIT lecture notes](https://math.mit.edu/~goemans/18438F09/lec11.pdf) about matroid intersection including all the theory, that is required to construct and prove being optimal algorithm of matroid intersection, also it’s running time and Cunningham optimization. Includes additional information of weighted case problem and matroid unions.↵
4. [More MIT lecture notes](http://math.mit.edu/~goemans/18433S11/matroid-intersect-notes.pdf) about matroid intersection, but this one is more theoretical and contains different information from the previous source.↵
5. [Article](https://web.cs.elte.hu/egres/tr/egres-08-10.pdf) that contains long formula-heavy proof from the beginning. ↵
↵
Thanks for reading. I hope this article will help to those, who want get started with matroid theory in competitive programming.↵
↵
↵
↵
↵
Hello, CodeForces.↵
↵
I think that matroids are beautiful and powerful concept, however, not really well known in competitive programming.↵
↵
I’ve discovered matroids at 2019 Petrozavodsk Winter Training Camp. There was a problem that clearly cannot be solved using usual techniques I knew, editorial for this problem was just these three words “just matroid intersection”. Back then it took me more than 2 days of upsolving to find all the information and details I need and implement solution that gets AC on this. And it took way longer to actually understand why does it work and exactly how does it work. (I still hesitate in some details.)↵
↵
Of course, it is not hard to google up all the definitions and some related articles, but in my opinion they all are focused more on mathematical part of theory, strict proofs in some not really obvious but short ways, and observing only key points in whole theory, omitting a lot of intermediate results, logical steps and examples. In some article I’ve encountered this heavy-formula proof:↵
↵
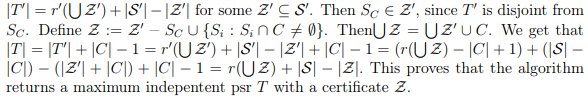↵
↵
That was nowhere close to being clear for me. (Probably I’m not mathematician enough, yet.) But still, I’m sure there is a way to make this more clear and detailed.↵
↵
I am sure, there are a lot of people in CP who will also like to get familiar with matroids. So, I’ve decided to review this topic from very beginning focusing more on explanations, logical steps and providing more examples. This is the goal of this article, and you do not need to know anything about matroids beforehand.↵
↵
[cut]↵
↵
.↵
↵
**Prerequisites.** You are not required to know well everything listed here, but it is good to be familiar with some of these concepts for better and faster understanding:↵
↵
1. Basics of set theory and set operations↵
2. Spanning trees in graphs↵
3. Matchings in bipartite graphs↵
4. Linear independence in vector spaces↵
5. Rank and basis of set of vectors↵
6. Gaussian elimination↵
7. Kruskal’s minimum spanning tree algorithm↵
8. Kuhn’s bipartite matching algorithm↵
9. Enjoying discrete math↵
↵
_All the information that used in this article is my own understanding of this topic, that I’ve learned from other articles found on the web. And as we know, proof by passing various tests is not a proper proof. So if you find something illogical or wrong, that should mean that I’ve made a mistake or misinterpret something, please point it out._↵
↵
What matroid is?↵
------------------↵
↵
Matroid is a structure that abstracts and generalizes the notion of linear independence in vector spaces.↵
↵
Here goes the formal definition. Matroid is a pair $\left\langle X, I \right\rangle$ where $X$ is called ground set and $I$ is set of all _independent_ subsets of $X$. In other words matroid $\left\langle X, I \right\rangle$ gives a classification for each subset of $X$ to be either _independent_ or _dependent_ (included in $I$ or not included in $I$).↵
↵
Of course, we are not speaking about arbitrary classifications. These $3$ properties must hold for any matroid:↵
↵
1. Empty set is independent.↵
2. Any subset of independent set is independent.↵
3. If independent set $A$ has smaller size than independent set $B$, there exist at least one element in $B$ that can be added into $A$ without loss of independency.↵
↵
These are _axiomatic properties_ of matroid. To prove that we are dealing with matroid, we generally have to prove these three properties.↵
↵
For example, explicit presentation of matroid on ground set $\\{x, y, z\\}$ which considers $\\{y, z\\}$ and $\\{x, y, x\\}$ to be dependent and marked red. Other sets are independent and marked green.↵
↵
↵
↵
From this definition we can derive some other important concepts (examples for all these concepts will be shown later, along with examples of matroids):↵
↵
**Bases.** Any independent set of maximum size is a basis of given matroid. In other words there is not element that can be added to a basis without loss of independency. All bases have equal size (otherwise we can add something to smaller basis from greater basis by third axiomatic property). Directly from previous, no basis is a subset of other basis. Any independent set is a subset of some basis (by third property we can continue increasing its size until reaching some basis), so it is enough to only know about all bases of matroid to completely describe it.↵
↵
**Circuits.** Dependent set is a circuit if all subsets (excluding whole set) of this set are independent. In other words, circuit is dependent set, that does not allow removing any of its elements without gaining independence. No circuit is a subset of another circuit (otherwise we can remove some elements from greater circuit without removing dependence). ↵
↵
Another important property of circuits, symmetric difference of two different circuits always contain a circuit. Symmetric difference of two sets contains all elements that are included only in one of the sets (formally, $A \Delta B = (A \setminus B) \cup (B \setminus A)$). This property is related to cycle spaces, in case of matroids this can be generalized to “circuit spaces”.↵
↵
**Ranks. Ranking function.** Rank of matroid is size of its bases. But we can directly refer it as size of the basis, why would we need specific definition for such thing? Yes, this is not really a flexible thing (we can refer it as size of basis), to make it more flexible we can define ranking function $r(S)$ that tells maximum size of independent subset for some $S$, which is subset of ground set. Value of ranking function on some subset can be referred as rank of this subset in matroid. This information about subsets can be very helpful in many situations. Some properties of ranking functions: ↵
↵
1. Rank of subset cannot be greater than size of this subset.↵
2. Rank of independent subset is size of this subset.↵
3. Rank of whole ground set is equal to rank of matroid. Rank of empty set is $0$.↵
4. Rank of any subset of set $S$ is not greater than rank of $S$.↵
5. Including $1$ element into set can only increase its rank by $1$ or leave it unchanged. (formally, for some set $S$ and element $x \notin S$ we have $r(S) \leq r(S \cup \\{x\\}) \leq r(S)+1$)↵
6. Ranking function of matroid is submodular. If we have two sets $A$ and $B$, moving all elements that are present in $B$ but not present in $A$ from $B$ to $A$ will not improve sum of ranks of both sets. Formally, $r(A) + r(B) \geq r(A \cup B) + r(A \cap B)$. In general element will not contribute more to a rank if it is moved to a set with additional elements. This might get more clear if explicitly split $A$ and $B$ into $A’ = A \setminus B$, $C’ = A \cap B$ and $B’ = B \setminus A$ and write it in a form $r(A’ \cup C’) + r(B’ \cup C’) \geq r(A’ \cup B’ \cup C’) + r(C’)$. See pictures below for example:↵
↵
↵
↵
Speaking informally, principle “it is better not to puts many eggs into one basket” works here.↵
↵
**Independence oracle.** Speaking about classifications of subsets, we usually cannot afford storing it as some information about each subset (it will result in exponential memory consumption). We need some other tools to test subsets for independence. If matroid is defined as a consequence of relations among elements in some other structure, we usually (probably, always?) can find algorithm with polynomial running time to test some subset of elements for independence. As we would like to abstract concept of matroids and use them regardless of their underlying independence mechanism, we can define _independence oracle_ as subroutine that tests some subset for independence. And we can measure running time of some algorithms as the number of _oracle calls_. (However, in practice we cannot completely forget about this, because we will miss great opportunities to optimize related algorithms.)↵
↵
#### Examples↵
↵
There are matroids of different types. There are some examples:↵
↵
**Uniform matroid.** Matroid that considers subset $S$ independent if size of $S$ is not greater than some constant $k$ ($|S| \leq k$). Simplest one, this matroid does not really distinguish elements of ground set in any form, it only cares about number of taken elements. All subsets of size $k$ are bases for this matroid, all subsets of size $(k+1)$ are circuits for this matroid. We can also define some specific cases of uniform matroid: ↵
↵
1. Trivial matroid. $k = 0$. Only empty set is considered independent, any element of ground set is considered dependent (any combination of ground set elements is also considered dependent as a consequence).↵
2. Complete matroid. $k = |X|$. All subsets are considered independent including complete ground set itself.↵
↵
**Linear (algebra) matroid.** Ground set consists of vectors of some vector space. Set of vectors is considered independent if it is linearly independent (no vector can be expressed as linear combination of other vectors from that set). This is the matroid from which whole matroid theory originates from. Linear bases of vector set are bases of matroid. Any circuit of this matroid is set of vectors, where each vector can be expressed as combination of all other vectors, but this combination involves all other vectors in circuit. Independence oracle for this matroid can be based on gaussian elimination.↵
↵
**Colorful matroid.** Ground set consists of colored elements. Each element has exactly one color. Set of elements is independent if no pair of included elements share a color. Rank of a set is amount of different colors included into a set. Bases of this matroid are sets that have exactly one element of each color. Circuits of this matroid are all possible pairs of elements of the same color. Colors can be enumerated with integers for practical purposes.↵
↵
**Graphic matroid.** This matroid is defined on edges of some undirected graph. Set of edges is independent if it does not contain a cycle. This type of matroids is the greatest one to show some visual examples, because it can include dependent subsets of a large size and can be represented on a picture at the same time. If graph is connected then any basis of this graph is just a spanning tree of this graph. If graph is not connected then basis is a forest of spanning trees that include one spanning tree for each connected component. Circuits are simple loops of this graph. Independence oracle for this matroid type can be implemented with DFS, BFS (start from each vertex in graph and check that no edge connect a vertex with already visited one) or DSU (keep connected components, start with disjoint vertices, join by all edges and ensure that each edge connected different components upon addition). Here is an example of circuit combinations property in graphic matroid:↵
↵
↵
↵
**Truncated matroid.** We can limit rank of any matroid by some number $k$ without breaking matroid properties. For example, base of truncated colorful matroid is set of elements that include no more than $k$ different colors and all colors are unique. Base of truncated graphic matroid is acyclic set of edges that leaves at least $(n-k)$ connected components in the graph (where $n$ is amount if vertices in a graph). This is possible because third matroid property does not only refer to bases of matroid, but to any independent set in matroid, and when all independent sets with sizes greater than $k$ are simultaneously removed, independent sets of size $k$ become new bases and for any lesser independent set can still find elements from each basis that can be added.↵
↵
**Matroid on a subset of ground set.** We can limit ground set of matroid to its subset without breaking matroid properties. This is possible because rules of dependence does not rely on specific elements being in ground set. If we remove an edge from a graph, we will still have a valid graph. If we remove an element from set (of vectors or colored elements) we will still get a valid set of some element of the same type, and rules will preserve. Now, we can also define rank of subset in matroid as a rank of matroid on a ground set limited to this subset.↵
↵
**Expanded matroid. Direct matroid sum.** We can consider two matroids as one big matroid without any difficulties if elements of ground set of first matroid does not affect independence, neither intersect with elements of ground set of second matroid and vise versa. Think of two graphic matroids on two connected graphs. We can unite their graphs together resulting in graph with two connected components, but it is clear that including some edges in one component have no effect on other component. This is called _direct matroid sum_. Formally, $M_1 = \left\langle X_1, I_1 \right\rangle, M_2 = \left\langle X_2, I_2 \right\rangle, M_1 + M_2 = \left\langle X_1 \cup X_2, I_1 \times I_2 \right\rangle$, where $\times$ means cartesian product of two sets. You can unite as many matroids of as many different types without restrictions as you want (if you can find some use for the result).↵
↵
_This is not the only types of matroids. You can find more information about useful matroid types or even create your own._↵
↵
#### Rado-Edmonds algorithm↵
↵
Now, speaking about practical purposes of matroids. We have the following problem: we need to find a basis in matroid $M = \left\langle X, I \right\rangle$. How do we approach this problem efficiently?↵
↵
According to third matroid property, if we have some independent set $S$ which size is less than size of a basis we can find some element $x$ that can be added to $S$ without loss of independence. So, we can start with empty set that is guaranteed to be independent and add elements one-by-one performing a linear scan over ground set to find next element to add. If we denote $n$ as a size of ground set $X$ and $r$ as a rank of $M$ we have algorithm that runs in $\mathcal{O}(r \cdot n)$ _oracle calls_.↵
↵
But we can do it better, notice that if some element $x$ wasn’t added into $S$ on some step it will never be possible to include it on any future step, because if $S \cup \\{x\\}$ was considered dependent on some step it includes some circuit $C$ and we never exclude elements in this algorithm, so any future expanded version of $S$ will also confirm $S \cup \\{x\\}$ to include some circuit $C$ and be dependent. So we can find a basis in one single scan, if we will take elements greedily (include element into $S$ if it does not break independence of $S$ at the step). So, we have improved runtime to $\mathcal{O}(n)$ _oracle calls_.↵
↵
But, what about weighted case? Let each element $x$ of the ground set have some weight $w(x)$. We want to find a basis in our matroid with minimal sum of weights.↵
↵
_You probably know about Kruskal’s minimum spanning tree algorithm, which actually solves the problem for graphic matroid, but how do you prove it without recalling some of matroid properties?_↵
↵
Keeping in mind greedy ideas, we can try to connect results of $k$-th and $(k+1)$-th steps of algorithm to show something. Let’s assume that $A$ is the minimum weight independent set of size $k$ and $B$ is minimum weight independent set of size $(k+1)$. By third matroid property, we have at least one element $y$ in $B$ that can be added into $A$ without loss of independency. So, we have sets $B \setminus \\{y\\}$ of size $k$ and $A \cup \\{y\\}$ of size $(k+1)$. As we know what are minimum weighted sets, we can write down:↵
↵
$A \leq B \setminus \\{y\\}$↵
↵
$B \leq A \cup \\{y\\}$↵
↵
we add $y$ to both sets in first inequality and get:↵
↵
$A \cup \\{y\\} \leq (B \setminus \\{y\\}) \cup \\{y\\}$↵
↵
$A \cup \\{y\\} \leq B$↵
↵
we can see that↵
↵
$B \leq A \cup \\{y\\} \leq B$↵
↵
which means↵
↵
$B = A \cup \\{y\\}$↵
↵
In other words, we can get minimum weight independent set of size $(k+1)$ from minimum weight independent set of size $k$ by including some element $y$ into it which will not break independence. What if we have multiple of such elements $y$? Greedy answer, $y$ with minimum weight.↵
↵
Combining this with previous result we can present algorithm that will find basis with minimum sum of weights:↵
↵
1. Sort elements of ground set by ascending weight↵
2. Start with empty set $S$↵
3. Iterate elements of ground set in sorted order, at each step include current element into $S$ if it does not make $S$ dependent ↵
↵
Running time is $\mathcal{O}(n \cdot log(n))$ unit operations for sort plus $\mathcal{O}(n)$ _oracle calls_.↵
↵
This is Rado-Edmonds algorithm. As an example for specific matroid type we have Kruskal’s minimum spanning tree algorithm, mentioned above.↵
↵
If finding a basis of any matroid is done greedily and matroids are about generalizing things, probably we can prove that all greedy problems can be reduced to finding a base of some matroid? Well, no. ↵
↵
In greedy solutions we can sometimes not only sort elements, but also create additional elements in process or use some specific comparators or skip / take conditions. Even if we forget about weights and put some additional constraints, we can only use matroids in some specific cases. In general, if you want to prove that matroids are applicable here, you can focus on proving axiomatic properties.↵
↵
Matroid intersection↵
------------------↵
↵
And you may ask “Why would we ever need all these generalizations, if it does not invent anything new, anything that is not covered with other more situational and problem-specific algorithms?” Well, there are some problems that are extremely hard (in my opinion) to solve without using these generalizations. One of these problems is the problem of matroid intersection.↵
↵
More detailed, this problem should be called “finding largest common independent set in intersection of two matroids”. Formally, we are given two matroids $M_1 = \left\langle X, I_1 \right\rangle$ and $M_2 = \left\langle X, I_2 \right\rangle$ and we want to find any set $S$ with $\max\limits_{S \in I_1 \cap I_2} |S|$. In other words largest possible $S$ that is considered independent by both matroids.↵
↵
We can show multiple examples of such problems. I mostly like these: ↵
↵
**Colorful spanning tree.** You are given a graph and a color for each edge in that graph. You have to find spanning tree of this graph that has no more than one edge of each color. Clearly, matroid classifications are “set of edges contains no more than two edges of a same color” and “set of edges contains no cycles”.↵
↵
**Colorful linear basis.** You are given a set of vectors in some vector space and a color for each given vector. You have to find a basis of given set of vectors that includes no more than one vector of each color. Here we go with linear independence on one and unique colors on the other.↵
↵
**Bipartite graph maximum matching.** Well known problem, you are given bipartite graph find subset of edges of maximum size such that no pair of edges from this subset share a vertex. Might not be obvious, what should we do here, but think of easier version of the problem: replace “no pair share a vertex” with ”no pair share a vertex from the left part”. Now we can easily solve that problem with picking one edge for each vertex on a left part with non-zero power, also we can show that it can be done greedily and it forms a proper matroid. And as we have two parts in given graph, we can obtain second matroid for the right part symmetrically and solve intersection problem.↵
↵
Wait, but why exactly two matroids? What about intersecting more? Well, that significantly expands the number of problems that can be reduced to intersection of multiple matroids. In fact this stuff becomes general enough to offer a solution for Hamiltonian path problem. Given directed graph, intersect these three matroids on ground set of edges of a graph:↵
↵
1. Ensure each vertex has at most $1$ outcoming power (can be represented as colorful matroid, paint edges that come out of the same vertex into one color)↵
2. Ensure each vertex has at most $1$ incoming power (just as previous one)↵
3. Ensure there is no loops (forget about edges direction and check that edges form a forest of spanning trees)↵
↵
And… it is NP-complete. Which means we have no idea how to solve it in polynomial time.↵
↵
So, returning to two matroids. How can we approach this problems? Bruteforce exponential solution is pretty obvious (check all the sets from either $I_1$ or $I_2$). Difficulties start from the point that $\left\langle X, I_1 \cap I_2 \right\rangle$ is not guaranteed to form a proper matroid. As we know finding a basis of any matroid can be done greedily and, well, randomly picking edges into a matching is not a great way to solve it. ↵
↵
_Probably, you know about Kuhn’s bipartite matching algorithm and using the fact that these problems are similar you may somehow come to a general solution._↵
↵
We need some observations here. Consider single matroid $M = \left\langle X, I \right\rangle$ and some basis $B$ in it (and this basis is not unique, otherwise that would be a trivial case). We can always find some element $p$ that can be excluded from $B$ and some other element $q$ can be included in $B$ instead, so that it will not break independence (formally, $B \setminus \\{p\\} \cup \\{q\\} \in I$). ↵
↵
For example, considering $M$ is graphic matroid of the following graph, red and yellow edges form a spanning tree, which is a basis of $M$. ↵
↵
↵
↵
We can exchange yellow edge for one of blue edges to get one-edge-different spanning tree. Let’s call this _exchange_ operation. Let’s see if we can find a sequence of exchange operations that will change our basis $B$ to some other valid basis of matroid $M$. ↵
↵
For example, there are two different spanning trees of the same graph:↵
↵
↵
↵
We can get green tree from red tree with this sequence of exchanges:↵
↵
1. Exchange $(4,5)$ to $(1,5)$↵
2. Exchange $(4,8)$ to $(8,9)$↵
3. Exchange $(1,2)$ to $(2,3)$↵
4. Exchange $(3,4)$ to $(2,8)$↵
↵
Note, that swapped pairs and sequence of operations if important. We cannot exchange $(3,4)$ to $(2,8)$ earlier than $(1,2)$ to $(2,3)$ as it will result in leaving vertex $3$ isolated and creating a cycle in other part of a graph. Also, we cannot start with swapping $(4, 5)$ to $(2, 8)$.↵
↵
<spoiler summary="General algorithm for finding such sequence for graphic matroid">↵
↵
We have connected graph $G$ with $n$ vertices and two spanning trees of $G$, let’s call them white tree and black tree. We need to find some sequence of exchanges, than will one-by-one replace all white edges with all black edges, maintaining valid spanning tree after each operation.↵
↵
Notice that we have two equal criterias for forming a spanning tree from a set of $(n-1)$ edges:↵
↵
1. There is no cycles in it↵
2. All $n$ vertices are forming a single connected component with these edges↵
↵
So, we can focus only on one of them. We can check forming a single connected component.↵
↵
Root white spanning tree in some vertex $r$. Now there is at least one leaf (vertex that does not have any children) in white rooted tree. Consider any leaf $l$, it is connected by exactly one white edge with it’s parent and at least one black edge with some other vertex in $G$. Exchange this white edge to any black edge $(l, p)$ connected with this leaf. Now, we can see that our leaf will always be connected with $p$ for all the future operations (we do not want to cancel addition of black edge). As we care only about connectivity, compress $l$ and $p$ together. Now we have eliminated one vertex of a graph and one white edge and we now have a tree of $(n-1)$ vertices and $(n-2)$ white edges to exchange. ↵
↵
Again, we can find and eliminate one leaf with an edge to it as described above. We can continue doing it until we have single vertex left and all white edges are exchanged.↵
↵
</spoiler>↵
↵
It appears that we can _always_ find a sequence of exchange operations that will change our basis $B$ to _any_ other valid basis of matroid $M$ regardless of its type. This property is called “strong basis exchange” lemma and can be strictly proven in general form. We can generalize strong basis exchange to exchange of any independent sets of equal size, using the fact that they are valid bases of truncated version of matroid $M$.↵
↵
Knowing this, we want to find a good representation for all possible exchanges of ground set elements for some independent set $S$. Possible exchange is a relation between two elements: $x$ in $S$ and $y$ not in $S$. Well known fact, graphs are great way to represent relations between pairs of elements. We can define a structure called _exchange graph_ $D_M (S)$ of independent set $S$ in matroid $M$ as bipartite graph which contains edge $(x, y)$ if we can exchange $x$ to $y$ in $S$ without loss of independency (formally, $D_M (S)$ contains edge $(x, y)$ if $x \in S, y \in X \setminus S, S \setminus \\{x\\} \cup \\{y\\} \in I$). ↵
↵
For future I will refer part that contains elements in $S$ as “left” part and part that contains elements not in $S$ as “right” (that will be consistent with pictures).↵
↵
For example, there is some small graph $G$, red spanning tree $S$ and it’s exchange graph $D_M (S)$ on a graphic matroid $M$ of $G$:↵
↵
↵
↵
What does exchange graph offer to us? As first, consider some other independent set $T$ with equal size ($|S| = |T|$). There exists a perfect matching in $D_M (S)$ between $S \setminus T$ and $T \setminus S$ (between elements that are included in one set, but not included in other and their symmetry). By generalization of strong basis exchange we can swap elements one-by-one forming this perfect matching one edge per step.↵
↵
However, the opposite does not hold. We cannot guarantee that we can choose any matching in exchange graph, perform changes associated with selected edges and get independent set. Showing this for colorful matroid is trivial, we can change any element to element of unused color $c$, but we cannot change any two elements (not of color $c$) to two elements of color $c$ simultaneously. For graphic matroid consider the following acyclic red set of edges in given graph:↵
↵
↵
↵
We can exchange $(1, 2)$ to $(2, 3)$, symmetrically we can exchange $(5, 6)$ to $(3, 5)$. However we cannot perform these changes simultaneously.↵
↵
So, how can we understand whether changes can break things or they will preserve independence? We can notice that there are multiple ways to shuffle in some circuit $C$ into our independent set $S$ following exchange edges in $D_M (S)$. In example above we can also obtain the same circuit $(2-3-5-4)$ exchanging $(5, 6)$ to $(2, 3)$ and $(1, 2)$ to $(3, 5)$. Is it always the case? ↵
↵
Let’s try to construct a case when there is only one way to get a dependent set by following edges in $D_M (S)$. So, we are looking for some circuit $C$ to be formed in result of exchanges. We are not interested in exchange edges connecting two elements of $C$ as picking any of them into matching will immediately break circuit $C$ (there is no way to insert removed element back). This $C$ must have at least $2$ “vacant” places for elements to exchange into (at least two elements of $C$ must not be in $C$, $|C \setminus S| \geq 2$).If there is only “vacant” place there will be no edge in exchange graph to this element from any element that does not belong to $C$, because including this element will result in immediate completion of circuit $C$ and loss of dependency, this is not allowed by construction of exchange graph. So, we are generally looking for some structure of this form:↵
↵
↵
↵
Here, edges of independent set $S$ are marked red, edges not included in $S$ are marked gray, planned edge exchanges are marked with black arrows. Circuit $C$ contains all edges that form the border of yellow area ($C$ is $(3-5-7-8-6-4)$). Now, there are two ways to exchange edges to complete $C$. We want to find a way to restrict exchanging $(9, 10)$ to $(3, 4)$ and $(1, 2)$ to $(7, 8)$. The only way of doing this in terms of exchange graph is to construct additional circuit $L$ around $(3, 4)$ that would include edge $(1, 2)$ and not include $(9, 10)$ and put all edges from $L$ into $S$ except $(3, 4)$. This way exchanging $(9, 10)$ to $(3, 4)$ will lead to completing $L$, but exchanging $(1, 2)$ to $(3, 4)$ will still be possible. Symmetrically, we can construct circuit $R$ around $(7, 8)$.↵
↵
↵
↵
That’s it? Huh, something actually went wrong, as these actions led us to including a great circuit formed by all red edges into $S$. But $S$ must be independent. That happened because in terms of linear combinations some element $x$ plays the same role as some circuit $L$ that includes element $x$ without given element $x$ ($L \setminus \\{x\\}$). That is why it is actually called a circuit. Note, that vertices $3$ and $4$ can be connected with direct edge $(3,4)$, but also with remaining part of circuit $L$ which is $(3-11-1-2-12-4)$. Increasing the number of elements in $C$ not included in $S$ will not help, because we will still need a circuit connecting endpoints for each missing edge. Changing the type of matroid will not help either, properties of linear combinations will preserve.↵
↵
So, there is no way to restrict number of ways to include circuit $C$ to $1$ by edges of exchange graph. This means that there are _always_ at least $2$ ways to include any circuit into our set using exchange graph. That also means if there is only one way to get some other set $T$ from $S$ using $D_M (S)$, it is guaranteed for $T$ to be independent. In other words, we can say that $T$ will be independent if matching between $S \setminus T$ and $T \setminus S$ in $D_M (S)$ is _unique_.↵
↵
_All articles that I’ve seen prove this fact in other way that seems less obvious for me, but that may not be the case for you._↵
↵
Now that’s clear how we can reliably obtain some other independent sets of equal size. But remember that we need to do this for two matroids at the same time and also would like to somehow obtain the maximum size independent set, not just equal all the time.↵
↵
Considering two matroids $M_1 = \left\langle X, I_1 \right\rangle$ and $M_2 = \left\langle X, I_2 \right\rangle$ and some set $S$ independent for both ($S \in I_1 \cap I_2$), we can see that exchange graphs $D_{M_1} (S)$ and $D_{M_2} (S)$ have same vertices and bipartition. That’s good, these graphs only differ in set of edges, so we can meld them together resulting in a single graph with edges of two types. Let’s call this graph $D_{(M_1, M_2)} (S)$. Now we can say that some set $T$ is also independent for both matroids if there exists a perfect matching between $S \setminus T$ and $T \setminus S$ for both types of edges in $D_{(M_1, M_2)} (S)$. ↵
↵
For example, consider a problem of colorful spanning tree on this small colorful graph $G$ and multiple exchange graphs built for colorful spanning tree $S$ (marked with red). $M_1$ refers to graphic matroid, $M_2$ refers to colorful matroid.↵
↵
↵
↵
↵
↵
↵
↵
There are only two colorful spanning trees of this graph ($S = \\{(1, 2), (2, 3), (3, 4)\\}$ and $T = \\{(1, 3), (2, 3), (2, 4)\\}$) and there exist a perfect matching between $S \setminus T = \\{(1, 2), (3,4)\\}$ and $T \setminus S = \\{(1, 3), (2, 4)\\}$ in both types of edges of $D_{(M_1, M_2)} (S)$.↵
↵
There is a cool way to generate a perfect matching within two sets of edges in bipartite graph between two sets of edges in different parts. Orient one type of edges from left part to right, and second type of edges from right part to left, and find a cycle containing all required vertices. Take a look at the example:↵
↵
↵
↵
Each vertex in a loop touches exactly one odd and one even edge. Edges in a loop will have their types according to their parity. This loop will always have odd length, so decomposition into two perfect matchings in edges of different types is obvious.↵
↵
Now we need to think about increasing the size of our independent set $S$. In a single matroid if independent set $S$ is not a basis we can always find at least one element that can be added into $S$ without loss of independence (by the third axiomatic property of matroids). Now, let’s group all elements that can be added into $S$ keeping it independent in $M_1$ into set $Y_1$ (formally, $x \in Y_1$ if $x \notin S, S \cup \\{x\\} \in I_1$).The same for $Y_2$ in $M_2$.↵
↵
Let’s see what can we do with this information. Firstly, if there is an element $x$ that belongs to both $Y_1$ and $Y_2$, that’s the jackpot, perfect option to include in $S$ immediately! Secondly, if $Y_1$ is empty or $Y_2$ is empty we can conclude that we have reached the basis in one of matroids and no future growth available for $S$. ↵
↵
But what should we do in general case? Let’s orient edges in $D_{(M_1, M_2)} (S)$. Edges from $D_{M_1} (S)$ from left to right, edges from $D_{M_2} (S)$ from right to left and find a… cycle? No. A path from any vertex in $Y_1$ to any vertex in $Y_2$. This will serve us two purposes at the same time. But why and how is this supposed to work?↵
↵
Firstly, selecting a path without shortcuts guarantees us uniqueness of perfect matchings along the path. Until there is a shortcut for some path, let’s use it and then we will eventually end up with path, where the $i$-th vertex in that path is connected only with $(i+1)$-th and probably with any subset of previous vertices, but it is not considered to be a shortcut because graph is oriented. Let’s call path from any vertex in $Y_1$ to any vertex in $Y_2$ without shortcuts to be _augmenting path_. But members of $Y_1$ and $Y_2$ are both in a right part, so the path will have odd length, matching will not include all vertices from the right part. Well, yes, but it will include all vertices from the left part, and will not include one vertex from the right part. For edges of $D_{M_1} (S)$ matching will not include first vertex of augmenting path, for edges of $D_{M_2} (S)$ last vertex of the path will not be included.↵
↵
And here second purpose comes in play, which is increasing size of $S$. Let’s expand ground set of both matroids with one temporary vertex $t$ which is completely independent from all other elements for both matroids and include it into $S$. There will be an edge between $t$ and members of $Y_1$ in $D_{M_1} (S)$ and between $t$ and members of $Y_2$ in $D_{M_2} (S)$. So we can complete our augmenting path to cycle, connecting last vertex to $t$ and $t$ to first vertex. So, the whole picture will look like this (for clarity, only edges included into cycle are shown)↵
↵
↵
↵
There will be unique matching in this cycle, as a consequence of uniqueness of matching in selected path, so we can perform a set of exchanges associated with selected edges (in fact selected vertices). We have included a temporary vertex $t$, that will be removed from $S$ after performing selected exchanges. So we get an independent set $S$ on expanded matroids but without usage of $t$, which means we can forget about $t$ and say that we increased size of $S$ by $1$ performing these operations on original matroids.↵
↵
Now we established the way of increasing size of $S$ by one. So we can start with empty $S$ and go ahead until we are able to find valid augmenting path.↵
↵
Fine, but what about sufficiency? How can we show that we will not fail to augment our independent set earlier than reaching its maximum size? If either $Y_1$ or $Y_2$ is empty, that means we have reached basis in one of matroids and this is clearly the maximum for intersection (due to third axiomatic matroid property we can always find an element that can be added to independent set if it is smaller than basis).↵
↵
What about the case, when we haven’t reached any of bases, but fail to find augmenting path? We need some theory here. Consider some set $S$ that is independent for both matroids $M_1$ and $M_2$ with rank functions $r_1$ and $r_2$, respectively. Now split ground set $X$ into two parts $U$ and $X \setminus U$. Elements of $S$ that were split into the same part must be independent for both matroids, speaking in terms of ranking functions we can write down $4$ inequalities:↵
↵
1. $|S \cap U| \leq r_1(U)$↵
2. $|S \cap U| \leq r_2(U)$↵
3. $|S \cap (X \setminus U)| \leq r_1(X \setminus U)$↵
4. $|S \cap (X \setminus U)| \leq r_2(X \setminus U)$↵
↵
combining $1$ and $4$ we can get↵
↵
$|S \cap U| + |S \cap (X \setminus U)| \leq r_1(U) + r_2(X \setminus U)$↵
↵
$|S| \leq r_1(U) + r_2(X \setminus U)$↵
↵
considering all possible splits (all possible $U$) and independent set $S$ of maximum size we get↵
↵
$\max\limits_{S \in I_1 \cap I_2} |S| \leq \min\limits_{U \subseteq X} (r_1(U) + r_2(X \setminus U))$↵
↵
Seems complicated enough, but we are entering all these difficulties to show reaching limit. If we can show equality that will confirm that we have reached this limit and cannot get any better result. So, we want to prove:↵
↵
$\max\limits_{S \in I_1 \cap I_2} |S| = \min\limits_{U \subseteq X} (r_1(U) + r_2(X \setminus U))$↵
↵
This theoretical limit is known as Edmonds-Lawler theorem or matroid intersection min-max relation. ↵
↵
Note, that with equality we do not care about minimum in the right part, it is enough for us for find any partition $U$ that will satisfy equality (in fact, that will be the minimum because right part cannot be less than left). We want to analyze the case, when we have no path from $Y_1$ to $Y_2$, so we can consider a split that is based on reachability of $Y_2$. Let vertex $x$ be included in $U$ if there is a path from $x$ to some vertex in $Y_2$. Now, we can split equality back↵
↵
$|S| = |S \cap U| + |S \setminus U| = r_1(U) + r_2(X \setminus U)$↵
↵
into↵
↵
$|S \cap U| = r_1(U)$↵
$|S \setminus U| = r_2(X \setminus U)$↵
↵
Suppose $r_1(U) > |S \cap U|$, that would mean that there exists another independent set $T$ in $U$ which is larger than $S \cap U$. By matroids property, there exists some element $x$ in $T$ that can be added into $S \cap U$ without loss of independence in $M_1$, generalizing $U$ to $X$ we cannot guarantee that $S \cup \\{x\\}$ will be independent in $M_1$, but it will include at most one circuit $C$ that will have some element $y$ not from $U$ (otherwise we cannot satisfy existence of greater independent set $T$ in $U$). If there is no circuit $C$ then any element $y$ not from $U$ can be exchanged to add $x$. But that means that there exists directed edge $(y, x)$ in exchange graph $D_{(M_1, M_2)} (S)$, that would mean that we can reach $Y_2$ from $y$ through that edge and vertex $x$, but we made an assumption that $y$ is not in $U$, so there is no path from $y$ to $Y_2$. We got a contradiction, so that proves $r_1(U) = |S \cap U|$.↵
↵
Symmetrically, we can prove that $r_2(X \setminus U) = |S \setminus U|$. ↵
↵
These contradictions are visualized on pictures of exchange graph below. Set $U$ splits ground set $X$ into two parts (below and above purple line), vertex in $Y_2$ can be reached from each vertex below the line and cannot be reached from any vertex above the line. In other words there is no edge that comes from upper part and goes to lower part crossing purple line, which shows that red edge cannot exist.↵
↵
↵
↵
Proving both equalities, we prove Edmonds-Lawler theorem and prove that we always reach optimal solution with this algorithm.↵
↵
Matroid intersection problem can be generalized to weighted case. Also there are a lot of interesting related stuff that is worth mentioning, but this theoretical part is already vast and I do not want to make it even larger. Check resources from “Useful links” chapter for more.↵
↵
Implementation and complexity, oracles↵
------------------↵
↵
Now, we have all the theory we need to actually implement a solution for matroid intersection problem.↵
↵
Remember, we are given two matroids $M_1 = \left\langle X, I_1 \right\rangle$ and $M_2 = \left\langle X, I_2 \right\rangle$ with ranking functions $r_1$ and $r_2$ respectively and independence oracles with running times $C_1$ and $C_2$ respectively. We need to find largest set $S$ that is independent for both matroids.↵
↵
According to algorithm we need to start with empty $S$ and then repeat the following until we fail to do this:↵
↵
1. Build exchange graph $D_{(M_1, M_2)} (S)$↵
2. Find “free to include vertices” sets $Y_1$ and $Y_2$↵
3. Find augmenting path without shortcuts $P$ from any element in $Y_1$ to any element in $Y_2$↵
4. Alternate inclusion into $S$ of all elements in $P$↵
↵
Let $r$ be the size of the result, $r = |S|$. Let $n$ be the size of ground set, $n = |X|$. We can safely assume that $r \leq min(r_1(X), r_2(X))$ because common independent set cannot be larger than size of bases in both intersecting matroids. So, main loop (augmentation process) will be repeated $r$ times.↵
↵
On each iteration we have $4$ steps:↵
↵
1. Building exchange graph is actually checking presence of all edges in bipartite graph with partition $S$ and $X \setminus S$. We measure their sizes as $|S| = \mathcal{O}(r)$ and $|X \setminus S| = \mathcal{O}(n)$. Between each pair of vertices from different parts there are two edges possible (one is from left to right, other is from right to left). Checking their presence requires $1$ oracle call for both matroids. So checking presence all edges, will be $\mathcal{O}(r) \cdot \mathcal{O}(n) \cdot (C_1 + C_2) = \mathcal{O}(r \cdot n \cdot (C_1 \cdot C_2))$.↵
2. Building $Y_1$ requires $1$ first oracle call for each vertex from right part $X \setminus S$, that gives runtime $\mathcal{O}(n \cdot C_1)$. Symmetrically, building $Y_2$ requires $1$ first oracle call for each vertex from right part $X \setminus S$, that gives runtime $\mathcal{O}(n \cdot C_2)$. Combining we get $\mathcal{O}(n \cdot (C_1 + C_2)).$↵
3. Hm, finding “a path without shortcuts”. Shortest path will do the trick. So, here we go with breadth-first search. Runtime is $\mathcal{O}(V + E) = \mathcal{O}(n + r \cdot n) = \mathcal{O}(r \cdot n).$↵
4. That’s the fastest one. Size of the shortest path cannot be greater than number of vertices in the graph. So, runtime is $\mathcal{O}(n)$.↵
↵
Without any cross-steps optimizations we have total running time $\mathcal{O}(r^2 \cdot n \cdot (C_1 + C_2))$. That is already good enough for some problems, but we can definitely go further this result.↵
↵
We can easily see that bottleneck for this algorithm is step $1$. Also we can see that this step does not require checking independence in arbitrary sets. We only need to take some independent set $S$ and exchange one pair of elements at a time. In general we need to remove at most 1 element and add at most 1 element and then check independence.↵
↵
We can find optimized matroid-type-specific solutions:↵
↵
**Colorful matroid.** We have elements of different colors, check whether we have more than $1$ element at the same time. Number of different colors cannot exceed $n$, we can use count array that will in $\mathcal{O}(1)$ tell us number of included elements of $i$-th color, add and remove elements. We generally do not need to do anything specific here, $\mathcal{O}(1)$ check is obvious combination of these operations.↵
↵
**Graphic matroid.** We have a forest of spanning trees, we need to check that exchanging edges does not include a loop. ↵
↵
We can $r$ times remove one edge and enumerate connected components and for each vertex find a connected component this vertex belongs to in $\mathcal{O}(n)$, and then we can add edge if and only if that edge connects different connected components. This requires $\mathcal{O}(r \cdot n)$ to prepare and allows checking presence of edge in $\mathcal{O}(1)$. Great balance between prepare and query parts, but generally it doesn’t allow doing anything more and seems to require $\mathcal{O}(r \cdot n)$ memory.↵
↵
We can try another approach. If added edge connects two different trees it will not break independence. If it connects two vertices in the same tree, then there is a loop, so we need to remove some other edge from that tree that belongs to this loop. So, if we add edge that connects $(x, y)$ we are fine only if we remove some other edge that belongs to a unique path in a tree between $x$ and $y$. We can reduce checking presence of edge in exchange graph to one query to check that some edge $(x, y)$ belongs to a path between some vertices $a$ and $b$. We can approach this problem with binary lifting, resulting in $\mathcal{O}(n \cdot log(n))$ precalc and $\mathcal{O}(log(n))$ per edge. Memory consumption can be reduced to $\mathcal{O}(n \cdot log(n))$.↵
↵
I haven’t tested which one is better. I think that the first way should perform better in practice unless memory limit is a problem.↵
↵
**Linear matroid.** We have a set of independent vectors in some vector space. We need to check whether we can remove one vector and add another. General approach is gaussian elimination, well known runtime is $\mathcal{O}(r^2 \cdot m)$, where $m$ is amount of dimensions of vector space. If vector space is $\mathbb{Z}_2^m$ we can apply bitset optimization achieving $\mathcal{O}(\frac{r^2 \cdot m}{w})$, where $w$ is size of machine word. But we can check loss of independency after addition of a single vector to a set faster if we have calculated basis of this set, we can do it in $\mathcal{O}(r \cdot m)$, because we only need to eliminate a single vector. We cannot find a way to remove a vector from a set after gaussian elimination was applied (I guess we can do something, but that won’t be easy and fast). But we can precalculate bases for each vector that can be removed and then eliminate a single vector instead of a whole set of vectors. Resulting runtime will be $\mathcal{O}(r^3 \cdot m)$ precalc and $\mathcal{O}(r \cdot m)$ per edge.↵
↵
But algorithm-specific oracles is not the only possible optimization here.↵
↵
We can notice that roles of matroids in exchange graph are not completely symmetrical. But it does not matter for solving the original problem. So, we can try swapping M_1 with M_2, and this may affect the runtime.↵
↵
To find a shortest path in a graph in general we don’t need to know the whole structure of a graph. If our oracles don’t take profits of building whole exchange graph at a time we can build it lazily, we can check presence of edges only when BFS tries to use them. We might think that it just improves the constant factor but article referenced in links under number $3$ contains this:↵
↵
_Cunningham has shown that we can find a maximum independent set with $\mathcal{O}(r^{1.5} \cdot n)$ oracle calls. The idea is to take a shortest augmenting path each time._↵
↵
Turns out this optimization actually improves complexity. In total we need $\mathcal{O}(\sqrt{r})$ times less oracle calls, when we construct exchange graphs lazily.↵
↵
Problem “Pick Your Own Nim“↵
------------------↵
↵
Sadly, I only know one problem that is directly involves algorithms that operate explicitly with matroids. I do not count applications of Rado-Edmonds algorithms and usage of matroid theory in proofs of correctness.↵
↵
_If you know some interesting problems about matroids, it would be great if you share them in comments._↵
↵
This problem is [problem:102156D] from [contest:102156].↵
↵
Shortly, problem gives us few boxes with numbers and asks us to choose exactly one number from each box in such way that we cannot choose non-empty subset of selected numbers with xor-sum equal to $0$. Or say that this is impossible. (Statement involves information about Nim game and Sprague-Grundy theorem but all the information we need to solve this problem is given in statement, and we do not need to care about it.) ↵
↵
Key observation here is that we cannot choose subset of numbers with zero xor-sum if and only if these numbers form independent set as vectors in $\mathbb{Z}_2^{60}$. Now reduction to matroid intersection comes obvious: ↵
↵
1. we want our set of numbers to be linearly independent, so we can use linear matroid↵
2. we want to choose exactly one number from each box. Colorful matroid can do the trick: assign the same color for all numbers in one box, different colors for different boxes.↵
↵
Now we can find largest independent set for both matroids and check that each color is used.↵
↵
So, this is the example of colorful linear basis problem. Involving some optimizations it can be solved in $\mathcal{O}(\frac{r^4 \cdot 60}{w} + \frac{r^{2.5} \cdot 60 \cdot n}{w})$. Assuming $\frac{60}{w}$ is $1$ or a small constant we can simplify it to $\mathcal{O}(r^4 + r^{2.5} \cdot n)$. Considering $r \leq 60, n \leq 5000$ it is about $10^7$ operations.↵
↵
<spoiler summary="Solution source code">↵
↵
~~~~~↵
#include <bits/stdc++.h>↵
↵
using namespace std;↵
↵
typedef long long int Z2Vector;↵
↵
struct GroundSetElement {↵
int color;↵
Z2Vector vector;↵
bool in_independent_set;↵
int independent_set_position;↵
int bfs_parent;↵
};↵
↵
struct Z2Basis {↵
vector<Z2Vector> vectors;↵
↵
void add_vector(Z2Vector new_vector) {↵
vectors.push_back(new_vector);↵
}↵
↵
void reset() {↵
vectors.clear();↵
}↵
↵
int size() {↵
return vectors.size();↵
}↵
↵
void gaussian_elimination() {↵
for (int i = 0; i < size(); i++) {↵
for (int j = i; j < size(); j++) {↵
if (vectors[i] < vectors[j]) swap(vectors[i], vectors[j]);↵
}↵
↵
for (int j = i+1; j < size(); j++) {↵
vectors[j] = min(vectors[j], vectors[j] ^ vectors[i]);↵
}↵
}↵
}↵
↵
bool independent_with(Z2Vector new_vector) {↵
for (auto v : vectors) new_vector = min(new_vector, new_vector ^ v);↵
↵
return new_vector > 0;↵
}↵
};↵
↵
int n;↵
int m;↵
↵
int color_count;↵
bool color_used[60+60];↵
↵
vector<GroundSetElement> ground_set;↵
vector<int> independent_set; /// as indexes of ground set↵
Z2Basis basis; /// of independent set↵
Z2Basis basis_without[60+60];↵
↵
bool linear_oracle(int inserted) {↵
return basis.independent_with(ground_set[inserted].vector);↵
}↵
↵
bool linear_oracle(int inserted, int removed) {↵
int wi = ground_set[removed].independent_set_position;↵
↵
return basis_without[wi].independent_with(ground_set[inserted].vector);↵
}↵
↵
void prepare_linear_oracle() {↵
basis.reset();↵
↵
for (int i = 0; i < independent_set.size(); i++) {↵
basis_without[i].reset();↵
}↵
↵
for (int i = 0; i < independent_set.size(); i++) {↵
basis.add_vector(ground_set[independent_set[i]].vector);↵
for (int j = 0; j < independent_set.size(); j++) {↵
if (i != j) basis_without[j].add_vector(ground_set[independent_set[i]].vector);↵
}↵
}↵
↵
basis.gaussian_elimination();↵
for (int i = 0; i < independent_set.size(); i++) {↵
basis_without[i].gaussian_elimination();↵
}↵
}↵
↵
bool colorful_oracle(int inserted) {↵
int inserted_color = ground_set[inserted].color;↵
↵
return !color_used[inserted_color];↵
}↵
↵
bool colorful_oracle(int inserted, int removed) {↵
int inserted_color = ground_set[inserted].color;↵
int removed_color = ground_set[removed].color;↵
↵
if (!color_used[inserted_color]) return true;↵
↵
return inserted_color == removed_color;↵
}↵
↵
void prepare_colorful_oracle() {↵
for (int c = 0; c < color_count; c++) {↵
color_used[c] = false;↵
}↵
↵
for (auto idx : independent_set) {↵
color_used[ground_set[idx].color] = true;↵
}↵
}↵
↵
bool augment() {↵
prepare_linear_oracle();↵
prepare_colorful_oracle();↵
↵
const int SOURCE = -1;↵
const int NOT_VISITED = -2;↵
const int NOT_FOUND = -3;↵
↵
for (int i = 0; i < ground_set.size(); i++) {↵
ground_set[i].bfs_parent = NOT_VISITED;↵
}↵
↵
int endpoint = NOT_FOUND;↵
↵
queue<int> q;↵
↵
for (int i = 0; i < ground_set.size(); i++) {↵
if (colorful_oracle(i)) {↵
ground_set[i].bfs_parent = SOURCE;↵
q.push(i);↵
}↵
}↵
↵
while (q.size()) {↵
int cur = q.front();↵
q.pop();↵
↵
if (ground_set[cur].in_independent_set) {↵
for (int to = 0; to < ground_set.size(); to++) {↵
if (ground_set[to].bfs_parent != NOT_VISITED) continue;↵
if (!colorful_oracle(cur, to)) continue;↵
↵
ground_set[to].bfs_parent = cur;↵
q.push(to);↵
}↵
} else {↵
if (linear_oracle(cur)) {↵
endpoint = cur;↵
break;↵
}↵
↵
for (auto to : independent_set) {↵
if (ground_set[to].bfs_parent != NOT_VISITED) continue;↵
if (!linear_oracle(cur, to)) continue;↵
↵
ground_set[to].bfs_parent = cur;↵
q.push(to);↵
}↵
}↵
}↵
↵
if (endpoint == NOT_FOUND) return false;↵
↵
do {↵
ground_set[endpoint].in_independent_set ^= true;↵
endpoint = ground_set[endpoint].bfs_parent;↵
} while (endpoint != SOURCE);↵
↵
independent_set.clear();↵
for (int i = 0; i < ground_set.size(); i++) {↵
if (ground_set[i].in_independent_set) {↵
ground_set[i].independent_set_position = independent_set.size();↵
independent_set.push_back(i);↵
}↵
}↵
↵
return true;↵
}↵
↵
void solve() {↵
cin >> n;↵
for (int i = 0; i < n; i++) {↵
ground_set.emplace_back();↵
ground_set.back().color = i;↵
ground_set.back().in_independent_set = false;↵
↵
cin >> ground_set.back().vector;↵
}↵
↵
cin >> m;↵
for (int i = 0; i < m; i++) {↵
int k;↵
cin >> k;↵
while (k--) {↵
ground_set.emplace_back();↵
ground_set.back().color = n+i;↵
ground_set.back().in_independent_set = false;↵
↵
cin >> ground_set.back().vector;↵
}↵
}↵
↵
color_count = n+m;↵
↵
while (augment()) ;↵
↵
if (independent_set.size() < color_count) {↵
cout << "-1\n";↵
return;↵
}↵
↵
for (int i = n; i < ground_set.size(); i++) {↵
if (ground_set[i].in_independent_set) cout << ground_set[i].vector << "\n";↵
}↵
}↵
↵
int main() {↵
solve();↵
}↵
~~~~~↵
↵
</spoiler>↵
↵
Useful links↵
------------------↵
↵
Surely, you can find all the information in google with queries like “matroid”, “matroid theory”, “matroid intersection” and “matroid intersection algorithm”. But I will list all important sources of information that helped me to learn matroids and prepare this article.↵
↵
1. [Wikipedia matroid page](https://en.wikipedia.org/wiki/Matroid). English version of this page contains a lot of information about the definitions, examples and related problems. ↵
2. [NEERC IFMO Wiki Matroids category](https://neerc.ifmo.ru/wiki/index.php?title=Категория:Матроиды) of about 20 useful articles. Some of them do not explain thing in details, including only most important points, but you can find some great images related to the topic here. _This seems to be only in russian._↵
3. [MIT lecture notes](https://math.mit.edu/~goemans/18438F09/lec11.pdf) about matroid intersection including all the theory, that is required to construct and prove being optimal algorithm of matroid intersection, also it’s running time and Cunningham optimization. Includes additional information of weighted case problem and matroid unions.↵
4. [More MIT lecture notes](http://math.mit.edu/~goemans/18433S11/matroid-intersect-notes.pdf) about matroid intersection, but this one is more theoretical and contains different information from the previous source.↵
5. [Article](https://web.cs.elte.hu/egres/tr/egres-08-10.pdf) that contains long formula-heavy proof from the beginning. ↵
↵
Thanks for reading. I hope this article will help to those, who want get started with matroid theory in competitive programming.↵
↵
↵
↵






