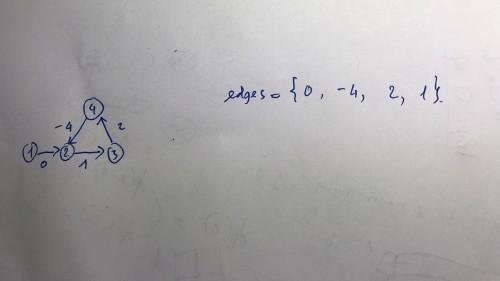I have solved UVa-10499 Traffic.
The problem ask to find out all shortest path from vertex 1, if vertices are affected by negative cycle, it means the shortest path become undefined and we print ?. I solved it with Bellman-Ford algorithm and it passed but I feel my approach is incorrect and I found a counter-example.

My approach: In the nth-relaxation, if vertices are shorten, I assign shortest path to them equal $$$-\infty$$$.

for(auto e:edges){
    int u, v, w; tie(u, v, w) = e;
    if (d[u]+w < d[v]) {
        d[v] = -INF;
    }
}

My fully solution: https://ideone.com/TfuoGz
For example, I have this graph and edges are stored in this order, the weight of edges represent the edges.

and in the n-th relaxation, I am just able to assign $$$-\infty$$$ to vertex 3, but vertex 2 and 4 are also affected by negative cycle.
Does the system test is weak or I understand something wrong? Could you suggest me the approach to solve this kind of problems.
Thank you!