[Апрельский кубок Санкт-Петербургской олимпиады по программированию 2020](https://codeforces.net/group/a6606NKaXI/contests) прошел вместо очной олимпиады Санкт-Петербурга для 3-7 классов (но мы планируем все-таки провести ее, когда карантин закончится!)↵
↵
Социальная дистанция (первая лига A)↵
------------------------------------↵
↵
Если $d\ge x$, то условие уже соблюдается, поэтому ответ 0, иначе ответ равен $x-d$.↵
↵
↵
Пример кода на языке Python:↵
↵
~~~~~↵
d = int(input())↵
x = int(input())↵
if d >= x:↵
print(0)↵
else:↵
print(x - d)↵
~~~~~↵
↵
Три оценки (первая лига B)↵
--------------------------↵
↵
Для того, чтобы сделать сумму второй и третьей оценки как можно больше, нужно стараться сделать первую оценку как можно меньше. ↵
↵
Если $n\le 11$, то можно сделать первую оценку равной 1, а остаток распределить между второй и третьей оценкой, только надо делать это аккуратно, чтобы обе оценки были от 1 до 5. Один из способов это сделать — разделить на две примерно равные части, как сделано в приведенном ниже коде.↵
↵
Если $n\ge 11$, то можно последние две оценки сделать равными 5, а остаток сделать первой оценкой.↵
↵
Пример кода на языке Python:↵
↵
~~~~~↵
n = int(input())↵
if n <= 11:↵
print(1, (n - 1) // 2, n // 2)↵
else:↵
print(n - 10, 5, 5)↵
~~~~~↵
↵
Делим конфетки (первая лига C, высшая лига A)↵
---------------------------------------------↵
↵
Для того, чтобы распределить конфеты между $n$ участниками так, чтобы они получили различное число конфет, нужно как минимум $s=1+2+\ldots\+n$ конфет. Эту сумму можно посчитать либо циклом, либо по формуле суммы арифметической прогрессии, как в коде ниже. Если у нас конфет меньше, чем $s$, то распределить не получится. Если же больше, чем $s$, то можно лишние конфеты отдать участнику на первом месте, и после этого все еще все будут получать различное число. Таким образом, нам нужно просто проверить, что $m\ge s$.↵
↵
Пример кода на языке Python:↵
↵
~~~~~↵
n = int(input())↵
m = int(input())↵
s = n * (n + 1) // 2↵
if m >= s:↵
print("Yes")↵
else:↵
print("No")↵
~~~~~↵
↵
Игрушечная машинка (первая лига D, высшая лига B)↵
-------------------------------------------------↵
↵
Давайте переберем все секунды, когда двигалась машинка, и будем поддерживать переменную $v$ равной текущей скорости машинки. Каждый раз смотрим на очередной символ строки, и либо увеличиваем, либо уменьшаем $v$ на единицу. Одновременно с этим в переменной $l$ будем считать суммарное расстояние, которое проехала машинка. Для этого просто будем каждую секунду прибавлять к $l$ значение переменной $v$.↵
↵
Пример кода на языке Python:↵
↵
~~~~~↵
n = int(input())↵
s = input()↵
v = 0↵
l = 0↵
for c in s:↵
if c == '+':↵
v += 1↵
elif v > 0:↵
v -= 1↵
l += v↵
print(l)↵
~~~~~↵
↵
Пилообразная последовательность (первая лига E, высшая лига C)↵
--------------------------------------------------------------↵
↵
Задача получилась неожиданно сложной. Решение этой задачи — это жадный алгоритм. Посмотрим на первые два числа. Если для них условие $a_1 < a_2$ не выполняется, то для того, чтобы оно стало выполняться, нужно либо уменьшить первое число, либо увеличить второе. Оба действия приближают нас к результату одинаково, но второе (увеличение второго числа) так же приближает нас к соблюдению следующего условия ($a_2 > a_3$), если оно еще не выполнено, поэтому будем увеличивать второе число, а не уменьшать первое. Далее продолжим по той же схеме добиваться того, чтобы выполнялось второе условие, и т. д.↵
↵
В приведенном ниже коде в переменной $x$ мы вычисляем значение, до которого нужно увеличить или уменьшить элемент $a_i$, чтобы выполнялось условие для $a_{i-1}$ и $a_i$. Далее прибавляем к ответу число действий, которое нужно сделать, чтобы $a_i$ стало равным $x$, и затем заменяем $a_i$ на $x$.↵
↵
Пример кода на языке Python:↵
↵
~~~~~↵
n = int(input())↵
a = [int(x) for x in input().split()]↵
s = 0↵
for i in range(1, n):↵
if i % 2 == 1:↵
x = max(a[i], a[i - 1] + 1)↵
else:↵
x = min(a[i], a[i - 1] - 1)↵
s += abs(a[i] - x)↵
a[i] = x↵
print(s)↵
~~~~~↵
↵
Коллекционирование карт (первая лига F, высшая лига D)↵
------------------------------------------------------↵
↵
Для начала переведем все времена в числа (число секунд от полуночи). Далее перебираем все времена и храним последний момент, когда мы получили новую карту. Если очередной момент времени отличается от него как минимум на $x$, то мы получаем новую карту: увеличиваем счетчик и запоминаем новое время.↵
↵
↵
Пример кода на языке Python:↵
↵
~~~~~↵
n, x = map(int, input().split())↵
a = []↵
for i in range(n):↵
s = input()↵
a.append(int(s[0:2]) * 60 * 60 + int(s[3:5]) * 60 + int(s[6:8]))↵
↵
res = 1↵
t = a[0]↵
for i in range(n):↵
if a[i] >= t + x:↵
t = a[i]↵
res += 1↵
↵
print(res)↵
~~~~~↵
↵
Кролики (первая лига G, высшая лига E)↵
--------------------------------------↵
↵
Если немного поиграть и посмотреть, как могут двигаться кролики, то становится понятно, что кролики двигаются парами. Действительно, посмотрим на два самых правых кролика. Пусть это кролики A и B. Тогда сначала единственное действие, которое можно сделать — это A перепрыгивает через B. После этого A находится правее B, и единственное действие, которое может сделать кролик B — перепрыгнуть через A, и т. д. Таким образом, если кроликов нечетное число, то решения нет, потому что у самого левого кролика не будет пары. Иначе Разбиваем кроликов на пары и двигаем их вправо одну за другой.↵
↵
Пример кода на языке Python:↵
↵
~~~~~↵
n, k = map(int, input().split())↵
if k % 2 == 1:↵
print(-1)↵
exit()↵
↵
print((n - k) * k // 2)↵
for i in range(k // 2):↵
for j in range(n - k):↵
print(k + j - i * 2 - 1, end=" ")↵
~~~~~↵
↵
Падающие буквы (первая лига H, высшая лига F)↵
---------------------------------------------↵
↵
Есть много способов решать эту задачу, например такой. Будем двигаться по каждому столбцу $j$ снизу вверх, при этом будем хранить в переменной $k$ номер клетки, на которую должна упасть очередная буква. Изначально $k=n-1$ (нумерация с 0). Если видим букву, то перемещаем ее на клетку $k$ и уменьшаем $k$ на единицу. Проделываем такую операцию с каждым столбцом по отдельности, в результате получим нужную таблицу.↵
↵
Пример кода на языке Python:↵
↵
~~~~~↵
n, m = map(int, input().split())↵
a = [list(input()) for x in range(n)]↵
for j in range(m):↵
k = n - 1↵
for i in range(n - 1, -1, -1):↵
if a[i][j] != '.':↵
a[k][j], a[i][j] = a[i][j], a[k][j]↵
k -= 1↵
for i in range(n):↵
print("".join(a[i]))↵
~~~~~↵
↵
Прыжки (высшая лига G)↵
----------------------↵
↵
В этой задаче нужна небольшая математическая интуиция. ↵
↵
Давайте сначала поймем, для каких $k$ точно не получится допрыгать до точки $x$. Пусть $s=1+2+\ldots+k$. Если $s<x$, то допрыгать не получится, потому что суммарной дальности прыжков не достаточно. Во вторых, если четности $s$ и $x$ не совпадают, то мы также не сможем допрыгать, потому что на каждом прыжке четность меняется одинаково, вне зависимости от того, прыгаем мы влево или вправо. ↵
↵
Давайте найдем минимальное $k$, для которого не выполняется ни одно из этих ограничений. Покажем, что для этого $k$ существует способ допрыгать до $x$. Действительно, сделаем сначала все прыжки вправо, попадем в точку $s$. Теперь посмотрим на разность $d = s-x$, она должна быть четным числом. Сделаем прыжок на $d/2$ не вправо, а влево, тогда общее перемещение уменьшится как раз на $d$, и мы попадем в точку $x$ (на самом деле, нужно еще показать, что $d/2 \le k$, но это оставлю вам в качестве упражнения). ↵
↵
UPD: [user:BlackBear,2020-04-24] справедливо отметил, что в предыдущем абзаце написана неправда, может быть такое, что $d/2 > k$. В этом случае нужно развернуть несколько прыжков, в сумме составляющих $d/2$. ↵
↵
Более простой способ решения такой: найдем минимальное подходящее $k$, дальше будем двигаться с конца, от точки $x$, делая прыжки на $k, k-1, \ldots 1$, при этом каждый раз будем делать прыжок в сторону 0 (то есть, если стоим в положительной точке, двигаемся влево, а если в отрицательной, то вправо). Можно показать, что если выполняются оба условия на $k$, описанные выше, то этот процесс приведет нас в конце в точку 0. После этого осталось развернуть массив точек, которые мы посетили, и получим ответ.↵
↵
Пример кода на языке Python:↵
↵
~~~~~↵
x = int(input())↵
s = 1↵
k = 1↵
while s < x or s % 2 != x % 2:↵
k += 1↵
s += k↵
↵
p = [x]↵
for i in range(k, 1, -1):↵
if p[-1] > 0:↵
p.append(p[-1] - i)↵
else:↵
p.append(p[-1] + i)↵
p = p[::-1]↵
print(len(p))↵
print(*p)↵
~~~~~↵
↵
Развороты скобок (высшая лига H)↵
--------------------------------↵
↵
Это была действительно сложная задача, в ней требовалось не только разобраться, как работает предложенная модель, и придумать алгоритм, но и написать достаточно много кода.↵
↵
Для начала скажем, что ограничение на пять операций было избыточным, наше решение всегда будет делать не более трех операций (есть решение, которое делает не более двух операций, попробуйте его придумать сами).↵
↵
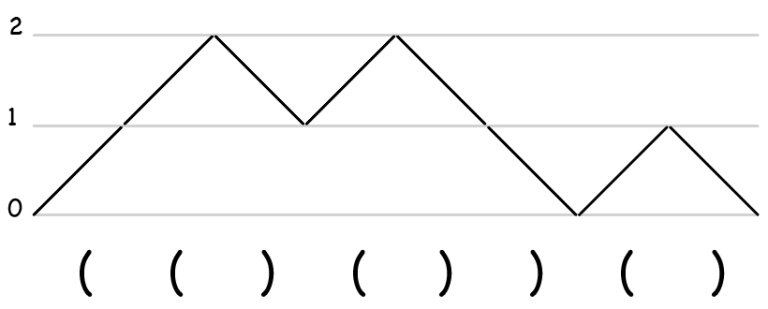
Чтобы было проще понять решение, давайте представлять скобочную последовательность в виде ломаной, которая начинается в точке 0, идет вверх, когда скобка открывается, и вниз, когда закрывается. Например, для скобочной последовательности `(()())()` получим такую ломаную:↵
↵
↵
↵
Скобочная последовательность будет правильной, если выполняется два условия: во-первых, ломаная должна заканчиваться на уровне 0 (то есть все открытые скобки закрылись), а во-вторых, ломаная не может уходить ниже 0 (это бы означало, что закрывается скобка, которая еще не была открыта до этого)↵
↵
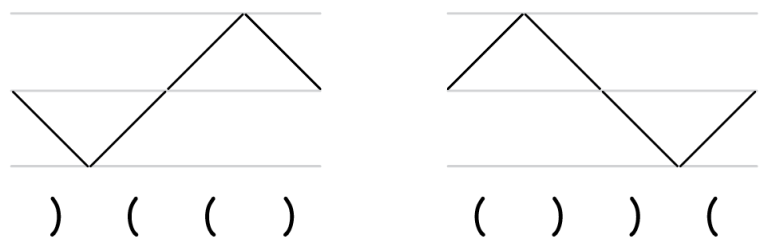
Теперь посмотрим, что же делает операция разворота отрезка. Она берет кусок ломаной и зеркально отражает его:↵
↵
↵
↵
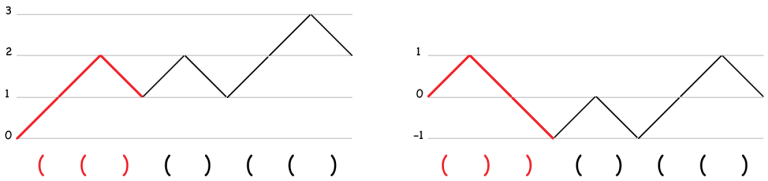
Давайте попробуем такими операциями сделать так, чтобы соблюдались оба условия. Сначала сделаем, чтобы соблюдалось первое. Для этого посмотрим, на какой высоте заканчивается ломаная, пусть это число $b$. Найдем такое начало ломаной, на котором высота ломаной равна $b/2$, и развернем это начало. После этого конец ломаной переместится в точку 0.↵
↵
↵
↵
Теперь сделаем так, чтобы соблюдалось второе условие. Для этого найдем самую низкую вершину ломаной, и развернем куски ломаной до нее и после нее. После этого оба условия будут соблюдаться, и мы получим правильную скобочную последовательность.↵
↵
↵
↵
Пример кода на языке Python:↵
↵
~~~~~↵
s = list(input())↵
n = len(s)↵
res = []↵
↵
↵
def reverse(l, r):↵
ss = s[l:r]↵
ss.reverse()↵
s[l:r] = ss↵
for i in range(l, r):↵
if s[i] == '(':↵
s[i] = ')'↵
else:↵
s[i] = '('↵
res.append("".join(s))↵
↵
↵
b = 0↵
for i in range(n):↵
if s[i] == '(':↵
b += 1↵
else:↵
b -= 1↵
↵
if b != 0:↵
c = 0↵
for i in range(n):↵
if s[i] == '(':↵
c += 1↵
else:↵
c -= 1↵
if c == b // 2:↵
reverse(0, i + 1)↵
break↵
↵
b = 0↵
minb = 0↵
mini = 0↵
for i in range(n):↵
if b < minb:↵
minb = b↵
mini = i↵
if s[i] == '(':↵
b += 1↵
else:↵
b -= 1↵
↵
if minb < 0:↵
reverse(0, mini)↵
reverse(mini, n)↵
↵
print(len(res))↵
for x in res:↵
print(x)↵
~~~~~↵
↵
↵
Социальная дистанция (первая лига A)↵
------------------------------------↵
↵
Если $d\ge x$, то условие уже соблюдается, поэтому ответ 0, иначе ответ равен $x-d$.↵
↵
↵
Пример кода на языке Python:↵
↵
~~~~~↵
d = int(input())↵
x = int(input())↵
if d >= x:↵
print(0)↵
else:↵
print(x - d)↵
~~~~~↵
↵
Три оценки (первая лига B)↵
--------------------------↵
↵
Для того, чтобы сделать сумму второй и третьей оценки как можно больше, нужно стараться сделать первую оценку как можно меньше. ↵
↵
Если $n\le 11$, то можно сделать первую оценку равной 1, а остаток распределить между второй и третьей оценкой, только надо делать это аккуратно, чтобы обе оценки были от 1 до 5. Один из способов это сделать — разделить на две примерно равные части, как сделано в приведенном ниже коде.↵
↵
Если $n\ge 11$, то можно последние две оценки сделать равными 5, а остаток сделать первой оценкой.↵
↵
Пример кода на языке Python:↵
↵
~~~~~↵
n = int(input())↵
if n <= 11:↵
print(1, (n - 1) // 2, n // 2)↵
else:↵
print(n - 10, 5, 5)↵
~~~~~↵
↵
Делим конфетки (первая лига C, высшая лига A)↵
---------------------------------------------↵
↵
Для того, чтобы распределить конфеты между $n$ участниками так, чтобы они получили различное число конфет, нужно как минимум $s=1+2+\ldots\+n$ конфет. Эту сумму можно посчитать либо циклом, либо по формуле суммы арифметической прогрессии, как в коде ниже. Если у нас конфет меньше, чем $s$, то распределить не получится. Если же больше, чем $s$, то можно лишние конфеты отдать участнику на первом месте, и после этого все еще все будут получать различное число. Таким образом, нам нужно просто проверить, что $m\ge s$.↵
↵
Пример кода на языке Python:↵
↵
~~~~~↵
n = int(input())↵
m = int(input())↵
s = n * (n + 1) // 2↵
if m >= s:↵
print("Yes")↵
else:↵
print("No")↵
~~~~~↵
↵
Игрушечная машинка (первая лига D, высшая лига B)↵
-------------------------------------------------↵
↵
Давайте переберем все секунды, когда двигалась машинка, и будем поддерживать переменную $v$ равной текущей скорости машинки. Каждый раз смотрим на очередной символ строки, и либо увеличиваем, либо уменьшаем $v$ на единицу. Одновременно с этим в переменной $l$ будем считать суммарное расстояние, которое проехала машинка. Для этого просто будем каждую секунду прибавлять к $l$ значение переменной $v$.↵
↵
Пример кода на языке Python:↵
↵
~~~~~↵
n = int(input())↵
s = input()↵
v = 0↵
l = 0↵
for c in s:↵
if c == '+':↵
v += 1↵
elif v > 0:↵
v -= 1↵
l += v↵
print(l)↵
~~~~~↵
↵
Пилообразная последовательность (первая лига E, высшая лига C)↵
--------------------------------------------------------------↵
↵
Задача получилась неожиданно сложной. Решение этой задачи — это жадный алгоритм. Посмотрим на первые два числа. Если для них условие $a_1 < a_2$ не выполняется, то для того, чтобы оно стало выполняться, нужно либо уменьшить первое число, либо увеличить второе. Оба действия приближают нас к результату одинаково, но второе (увеличение второго числа) так же приближает нас к соблюдению следующего условия ($a_2 > a_3$), если оно еще не выполнено, поэтому будем увеличивать второе число, а не уменьшать первое. Далее продолжим по той же схеме добиваться того, чтобы выполнялось второе условие, и т. д.↵
↵
В приведенном ниже коде в переменной $x$ мы вычисляем значение, до которого нужно увеличить или уменьшить элемент $a_i$, чтобы выполнялось условие для $a_{i-1}$ и $a_i$. Далее прибавляем к ответу число действий, которое нужно сделать, чтобы $a_i$ стало равным $x$, и затем заменяем $a_i$ на $x$.↵
↵
Пример кода на языке Python:↵
↵
~~~~~↵
n = int(input())↵
a = [int(x) for x in input().split()]↵
s = 0↵
for i in range(1, n):↵
if i % 2 == 1:↵
x = max(a[i], a[i - 1] + 1)↵
else:↵
x = min(a[i], a[i - 1] - 1)↵
s += abs(a[i] - x)↵
a[i] = x↵
print(s)↵
~~~~~↵
↵
Коллекционирование карт (первая лига F, высшая лига D)↵
------------------------------------------------------↵
↵
Для начала переведем все времена в числа (число секунд от полуночи). Далее перебираем все времена и храним последний момент, когда мы получили новую карту. Если очередной момент времени отличается от него как минимум на $x$, то мы получаем новую карту: увеличиваем счетчик и запоминаем новое время.↵
↵
↵
Пример кода на языке Python:↵
↵
~~~~~↵
n, x = map(int, input().split())↵
a = []↵
for i in range(n):↵
s = input()↵
a.append(int(s[0:2]) * 60 * 60 + int(s[3:5]) * 60 + int(s[6:8]))↵
↵
res = 1↵
t = a[0]↵
for i in range(n):↵
if a[i] >= t + x:↵
t = a[i]↵
res += 1↵
↵
print(res)↵
~~~~~↵
↵
Кролики (первая лига G, высшая лига E)↵
--------------------------------------↵
↵
Если немного поиграть и посмотреть, как могут двигаться кролики, то становится понятно, что кролики двигаются парами. Действительно, посмотрим на два самых правых кролика. Пусть это кролики A и B. Тогда сначала единственное действие, которое можно сделать — это A перепрыгивает через B. После этого A находится правее B, и единственное действие, которое может сделать кролик B — перепрыгнуть через A, и т. д. Таким образом, если кроликов нечетное число, то решения нет, потому что у самого левого кролика не будет пары. Иначе Разбиваем кроликов на пары и двигаем их вправо одну за другой.↵
↵
Пример кода на языке Python:↵
↵
~~~~~↵
n, k = map(int, input().split())↵
if k % 2 == 1:↵
print(-1)↵
exit()↵
↵
print((n - k) * k // 2)↵
for i in range(k // 2):↵
for j in range(n - k):↵
print(k + j - i * 2 - 1, end=" ")↵
~~~~~↵
↵
Падающие буквы (первая лига H, высшая лига F)↵
---------------------------------------------↵
↵
Есть много способов решать эту задачу, например такой. Будем двигаться по каждому столбцу $j$ снизу вверх, при этом будем хранить в переменной $k$ номер клетки, на которую должна упасть очередная буква. Изначально $k=n-1$ (нумерация с 0). Если видим букву, то перемещаем ее на клетку $k$ и уменьшаем $k$ на единицу. Проделываем такую операцию с каждым столбцом по отдельности, в результате получим нужную таблицу.↵
↵
Пример кода на языке Python:↵
↵
~~~~~↵
n, m = map(int, input().split())↵
a = [list(input()) for x in range(n)]↵
for j in range(m):↵
k = n - 1↵
for i in range(n - 1, -1, -1):↵
if a[i][j] != '.':↵
a[k][j], a[i][j] = a[i][j], a[k][j]↵
k -= 1↵
for i in range(n):↵
print("".join(a[i]))↵
~~~~~↵
↵
Прыжки (высшая лига G)↵
----------------------↵
↵
В этой задаче нужна небольшая математическая интуиция. ↵
↵
Давайте сначала поймем, для каких $k$ точно не получится допрыгать до точки $x$. Пусть $s=1+2+\ldots+k$. Если $s<x$, то допрыгать не получится, потому что суммарной дальности прыжков не достаточно. Во вторых, если четности $s$ и $x$ не совпадают, то мы также не сможем допрыгать, потому что на каждом прыжке четность меняется одинаково, вне зависимости от того, прыгаем мы влево или вправо. ↵
↵
Давайте найдем минимальное $k$, для которого не выполняется ни одно из этих ограничений. Покажем, что для этого $k$ существует способ допрыгать до $x$. Действительно, сделаем сначала все прыжки вправо, попадем в точку $s$. Теперь посмотрим на разность $d = s-x$, она должна быть четным числом. Сделаем прыжок на $d/2$ не вправо, а влево, тогда общее перемещение уменьшится как раз на $d$, и мы попадем в точку $x$ (на самом деле, нужно еще показать, что $d/2 \le k$, но это оставлю вам в качестве упражнения). ↵
↵
UPD: [user:BlackBear,2020-04-24] справедливо отметил, что в предыдущем абзаце написана неправда, может быть такое, что $d/2 > k$. В этом случае нужно развернуть несколько прыжков, в сумме составляющих $d/2$. ↵
↵
Более простой способ решения такой: найдем минимальное подходящее $k$, дальше будем двигаться с конца, от точки $x$, делая прыжки на $k, k-1, \ldots 1$, при этом каждый раз будем делать прыжок в сторону 0 (то есть, если стоим в положительной точке, двигаемся влево, а если в отрицательной, то вправо). Можно показать, что если выполняются оба условия на $k$, описанные выше, то этот процесс приведет нас в конце в точку 0. После этого осталось развернуть массив точек, которые мы посетили, и получим ответ.↵
↵
Пример кода на языке Python:↵
↵
~~~~~↵
x = int(input())↵
s = 1↵
k = 1↵
while s < x or s % 2 != x % 2:↵
k += 1↵
s += k↵
↵
p = [x]↵
for i in range(k, 1, -1):↵
if p[-1] > 0:↵
p.append(p[-1] - i)↵
else:↵
p.append(p[-1] + i)↵
p = p[::-1]↵
print(len(p))↵
print(*p)↵
~~~~~↵
↵
Развороты скобок (высшая лига H)↵
--------------------------------↵
↵
Это была действительно сложная задача, в ней требовалось не только разобраться, как работает предложенная модель, и придумать алгоритм, но и написать достаточно много кода.↵
↵
Для начала скажем, что ограничение на пять операций было избыточным, наше решение всегда будет делать не более трех операций (есть решение, которое делает не более двух операций, попробуйте его придумать сами).↵
↵
Чтобы было проще понять решение, давайте представлять скобочную последовательность в виде ломаной, которая начинается в точке 0, идет вверх, когда скобка открывается, и вниз, когда закрывается. Например, для скобочной последовательности `(()())()` получим такую ломаную:↵
↵
↵
↵
Скобочная последовательность будет правильной, если выполняется два условия: во-первых, ломаная должна заканчиваться на уровне 0 (то есть все открытые скобки закрылись), а во-вторых, ломаная не может уходить ниже 0 (это бы означало, что закрывается скобка, которая еще не была открыта до этого)↵
↵
Теперь посмотрим, что же делает операция разворота отрезка. Она берет кусок ломаной и зеркально отражает его:↵
↵
↵
↵
Давайте попробуем такими операциями сделать так, чтобы соблюдались оба условия. Сначала сделаем, чтобы соблюдалось первое. Для этого посмотрим, на какой высоте заканчивается ломаная, пусть это число $b$. Найдем такое начало ломаной, на котором высота ломаной равна $b/2$, и развернем это начало. После этого конец ломаной переместится в точку 0.↵
↵
↵
↵
Теперь сделаем так, чтобы соблюдалось второе условие. Для этого найдем самую низкую вершину ломаной, и развернем куски ломаной до нее и после нее. После этого оба условия будут соблюдаться, и мы получим правильную скобочную последовательность.↵
↵
↵
↵
Пример кода на языке Python:↵
↵
~~~~~↵
s = list(input())↵
n = len(s)↵
res = []↵
↵
↵
def reverse(l, r):↵
ss = s[l:r]↵
ss.reverse()↵
s[l:r] = ss↵
for i in range(l, r):↵
if s[i] == '(':↵
s[i] = ')'↵
else:↵
s[i] = '('↵
res.append("".join(s))↵
↵
↵
b = 0↵
for i in range(n):↵
if s[i] == '(':↵
b += 1↵
else:↵
b -= 1↵
↵
if b != 0:↵
c = 0↵
for i in range(n):↵
if s[i] == '(':↵
c += 1↵
else:↵
c -= 1↵
if c == b // 2:↵
reverse(0, i + 1)↵
break↵
↵
b = 0↵
minb = 0↵
mini = 0↵
for i in range(n):↵
if b < minb:↵
minb = b↵
mini = i↵
if s[i] == '(':↵
b += 1↵
else:↵
b -= 1↵
↵
if minb < 0:↵
reverse(0, mini)↵
reverse(mini, n)↵
↵
print(len(res))↵
for x in res:↵
print(x)↵
~~~~~↵
↵





