Note: This is **NOT** an official proof of the derived solution, as it is incoherent. It's rather a personal note for my illogical brain. It contains a derivation to the solution and the solution of [Educational Codeforces Round 87](https://codeforces.net/contest/1354) [C2](https://codeforces.net/contest/1354/problem/C2) at the bottom.↵
↵
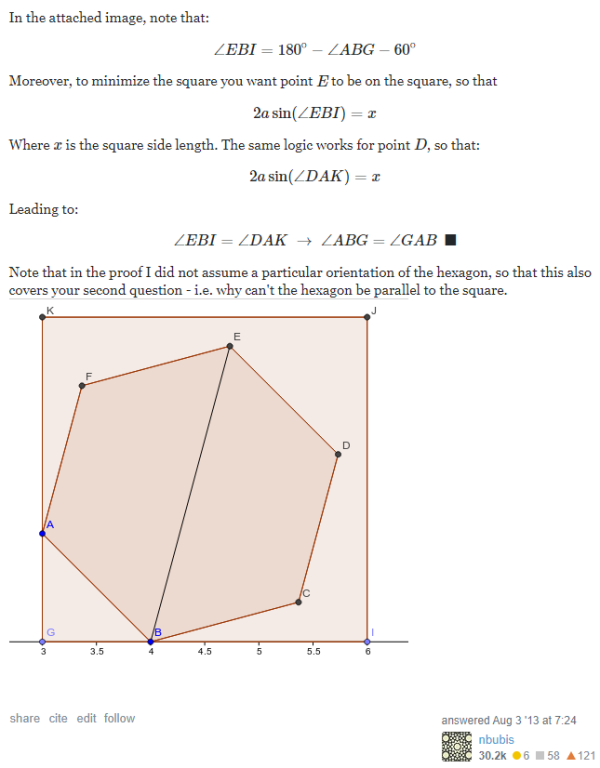↵
↵
Source: https://math.stackexchange.com/a/458593/496530↵
↵
From the above observation, 4 points of the polygon must be on the 4 sides of the minimal square. Each of 2 pairs, whose 2 points are on the opposite sides of the square, has the center of the polygon as its midpoint.↵
↵
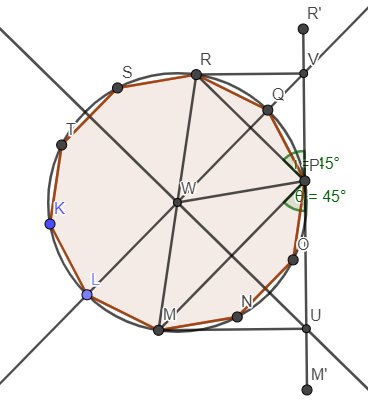
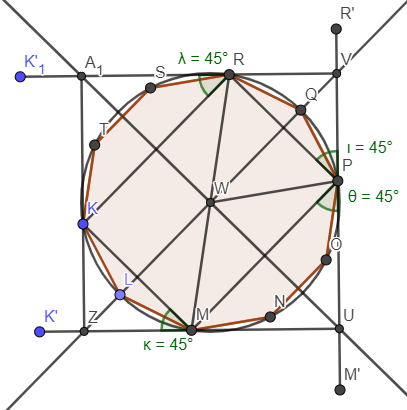
Below figures illustrate the minimal square when $n=5$. Half square on the left, full square on the right.↵
↵
↵
↵
↵
Recall:↵
$n$ is odd. Let $d$ be the length of the longest diagonal.↵
↵
Consider the point of interest to be $P$. Let's say $P$ is $k$ sides away from R, and $n-k$ sides away from M measured along the polygon circumference, where $k\in [0;n]$. Consider the left figure, $WU$ is the perpendicular bisector of $MP$, $WV$ is the perpendicular bisector of $RP$. Select $U$ where $\measuredangle{MPU}=45^{\circ}$. Select $V$ where $\measuredangle{RPV}=45^{\circ}$.↵
↵
WRecall that $n$ is odd, when $k=\lfloor\frac{n}{2}\rfloor+1$, $VU$ is the side of the minimal square containing the polygon.↵
↵
Let $d=RM$ be the diagonal of the polygon.↵
↵
But, $|VU|=d*\sin(\measuredangle{RMU})$, $|VU|$ should be smaller with smaller $\measuredangle{RMU}$ by using $k+1,k+2,..,n$. Why do these fail?↵
↵
Because, when $k>\lfloor\frac{n}{2}\rfloor+1$, from the way the square was built, some points are outside of the square.↵
↵
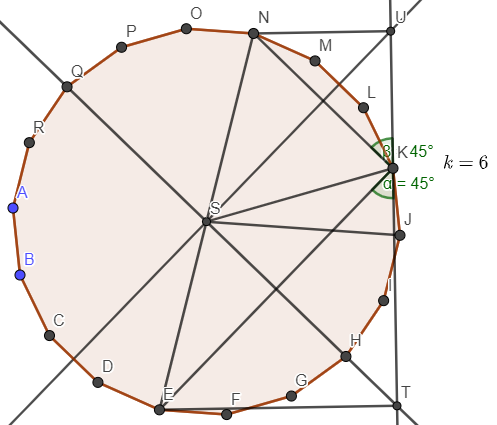
We can visualize these failed cases by considering 1 of them in the figure below where $n=9$, $k=6$ i.e. $k>\lfloor\frac{n}{2}\rfloor+1$:↵
↵
↵
↵
We can show that the point immediately below the chosen point ($K$) is out of the square by proving $\measuredangle{EKJ}>45^{\circ}$.↵
↵
**Proof:**↵
↵
Recall that $K$ is $k$ sides away from $E$ along the polygon circumference. In failed cases, $k>\lfloor\frac{n}{2}\rfloor+1$.↵
↵
$\measuredangle{SKE}=90^{\circ}-\frac{1}{2}.\frac{180^{\circ}.k}{n}$↵
↵
$\measuredangle{EKJ}=(180^{\circ}-\frac{180^{\circ}}{n}).\frac{1}{2}-\angle{SKE}=\frac{90^{\circ}}{n}.(k-1)$↵
↵
From $k>\lfloor\frac{n}{2}\rfloor+1$, since $n$ is odd and $k$ is integer, therefore $k-1>\frac{n}{2}$, so:↵
↵
$\measuredangle{EKJ}>\frac{90^{\circ}}{n}.\frac{n}{2}=45^{\circ} \blacksquare$↵
↵
Therefore $J$ (hence $F$) will be outside of the _bounding_ square.↵
↵
Now for the satisfied $k$:↵
↵
$k=\lfloor\frac{n}{2}\rfloor+1\implies\measuredangle{EKJ}=\frac{90^{\circ}}{n}.\lfloor\frac{n}{2}\rfloor<\frac{90^{\circ}}{n}.\frac{n}{2}=45^{\circ}$↵
↵
This guarantees $J$ (hence $F$ and other points in between) will be inside of the bounding square.↵
↵
End of reasoning.↵
↵
### Begin of derivation:↵
↵
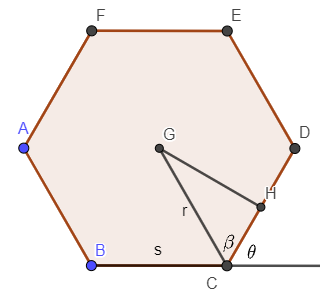↵
↵
Let:↵
↵
- $r$ be the radius of the circumscribed circle of the polygon↵
↵
- $s$ be the length of the polygon side↵
↵
- $\beta$ be the angle formed by a radius and a polygon side↵
↵
- $\theta$ be the exterior angle of the polygon↵
↵
- $m$ be the number of sides of the polygon↵
↵
- $v$, $u$ be the length of the upper and lower segment of the side of the minimal square, separated by the chosen vertex ($k$ polygon sides away from the top intersection of polygon & minimal square, in second figure: $v=PV$, $u=PU$)↵
↵
- $k=\lfloor\frac{n}{2}\rfloor$ which is symmetrical to $k=\lfloor\frac{n}{2}\rfloor+1$ in the polygon↵
↵
$\theta=\frac{360^{\circ}}{m}=\frac{360^{\circ}}{2n}$↵
↵
$r.\cos{\beta}=\frac{s}{2}{\implies}r=\frac{s}{2\cos{\beta}}=\frac{s}{2\cos{(\frac{\pi}{2}-\frac{\theta}{2})}}=\frac{s}{2\sin{(\frac{\theta}{2})}}$↵
↵
$v=r.\sin{(\frac{1}{2}.\frac{{\pi}k}{n})}.\sqrt{2}=r.\sin{(\frac{\pi}{2n}.\lfloor\frac{n}{2}\rfloor)}.\sqrt{2}$↵
↵
$u=r.\sin{(\frac{1}{2}.\frac{\pi(n-k)}{n})}.\sqrt{2}$↵
↵
$ans=v+u$↵
↵
For [Educational Codeforces Round 87](https://codeforces.net/contest/1354) [C2](https://codeforces.net/contest/1354/problem/C2):↵
↵
```c++↵
double r = 1.0/(2.0*sin(PI/(2*n)));↵
double v = r*sin(PI/(2*n)*(n/2))*sqrt(2);↵
double u = r*sin(PI/(2*n)*(n-n/2))*sqrt(2);↵
double ans = v + u;↵
```↵
↵
We can further simplify $v+u$:↵
↵
$v=r\sqrt{2}\sin{(\frac{\pi}{2n}.\frac{n-1}{2})}$↵
↵
$u=r\sqrt{2}\sin{(\frac{\pi}{2n}.(n-\frac{n-1}{2}))}$↵
↵
$ans=v+u=r\sqrt{2}[\sin{(\frac{\pi}{4}-\frac{\pi}{4n})}+\sin{(\frac{\pi}{4}+\frac{\pi}{4n})}]=\frac{\sqrt{2}}{2\sin{\frac{\theta}{2}}}.2\sin{\frac{\pi}{4}}\cos{\frac{-\pi}{4n}}$↵
↵
$\implies ans=\frac{s.\cos{\frac{\pi}{4n}}}{\sin{\frac{\pi}{2n}}}$↵
↵
As a solution to [1354C2](https://codeforces.net/contest/1354/problem/C2):↵
↵
```c++↵
double ans = cos(PI/(4*n))/(sin(PI/(2*n)));↵
```↵
↵
All figures above (except the 1st figure) were drawn in [GeoGebra Geometry](https://www.geogebra.org/geometry). Additionally, [GeoGebra](https://www.geogebra.org/) is a a free dynamic mathematics software containing several apps:↵
↵
- Graphing calculator↵
↵
- Geometry↵
↵
- 3D Calculator↵
↵
- CAS Calculator↵
↵
- Scientific Calculator↵
↵
↵
↵
Source: https://math.stackexchange.com/a/458593/496530↵
↵
From the above observation, 4 points of the polygon must be on the 4 sides of the minimal square. Each of 2 pairs, whose 2 points are on the opposite sides of the square, has the center of the polygon as its midpoint.↵
↵
Below figures illustrate the minimal square when $n=5$. Half square on the left, full square on the right.↵
↵
↵
↵
↵
$n$ is odd. Let $d$ be the length of the longest diagonal.↵
↵
↵
↵
Let $d=RM$ be the diagonal of the polygon.↵
↵
But, $|VU|=d*\sin(\measuredangle{RMU})$, $|VU|$ should be smaller with smaller $\measuredangle{RMU}$ by using $k+1,k+2,..,n$. Why do these fail?↵
↵
Because, when $k>\lfloor\frac{n}{2}\rfloor+1$, from the way the square was built, some points are outside of the square.↵
↵
We can visualize these failed cases by considering 1 of them in the figure below where $n=9$, $k=6$ i.e. $k>\lfloor\frac{n}{2}\rfloor+1$:↵
↵
↵
↵
We can show that the point immediately below the chosen point ($K$) is out of the square by proving $\measuredangle{EKJ}>45^{\circ}$.↵
↵
**Proof:**↵
↵
Recall that $K$ is $k$ sides away from $E$ along the polygon circumference. In failed cases, $k>\lfloor\frac{n}{2}\rfloor+1$.↵
↵
$\measuredangle{SKE}=90^{\circ}-\frac{1}{2}.\frac{180^{\circ}.k}{n}$↵
↵
$\measuredangle{EKJ}=(180^{\circ}-\frac{180^{\circ}}{n}).\frac{1}{2}-\angle{SKE}=\frac{90^{\circ}}{n}.(k-1)$↵
↵
From $k>\lfloor\frac{n}{2}\rfloor+1$, since $n$ is odd and $k$ is integer, therefore $k-1>\frac{n}{2}$, so:↵
↵
$\measuredangle{EKJ}>\frac{90^{\circ}}{n}.\frac{n}{2}=45^{\circ} \blacksquare$↵
↵
Therefore $J$ (hence $F$) will be outside of the _bounding_ square.↵
↵
Now for the satisfied $k$:↵
↵
$k=\lfloor\frac{n}{2}\rfloor+1\implies\measuredangle{EKJ}=\frac{90^{\circ}}{n}.\lfloor\frac{n}{2}\rfloor<\frac{90^{\circ}}{n}.\frac{n}{2}=45^{\circ}$↵
↵
This guarantees $J$ (hence $F$ and other points in between) will be inside of the bounding square.↵
↵
End of reasoning.↵
↵
### Begin of derivation:↵
↵
↵
↵
Let:↵
↵
- $r$ be the radius of the circumscribed circle of the polygon↵
↵
- $s$ be the length of the polygon side↵
↵
- $\beta$ be the angle formed by a radius and a polygon side↵
↵
- $\theta$ be the exterior angle of the polygon↵
↵
- $m$ be the number of sides of the polygon↵
↵
- $v$, $u$ be the length of the upper and lower segment of the side of the minimal square, separated by the chosen vertex ($k$ polygon sides away from the top intersection of polygon & minimal square, in second figure: $v=PV$, $u=PU$)↵
↵
- $k=\lfloor\frac{n}{2}\rfloor$ which is symmetrical to $k=\lfloor\frac{n}{2}\rfloor+1$ in the polygon↵
↵
$\theta=\frac{360^{\circ}}{m}=\frac{360^{\circ}}{2n}$↵
↵
$r.\cos{\beta}=\frac{s}{2}{\implies}r=\frac{s}{2\cos{\beta}}=\frac{s}{2\cos{(\frac{\pi}{2}-\frac{\theta}{2})}}=\frac{s}{2\sin{(\frac{\theta}{2})}}$↵
↵
$v=r.\sin{(\frac{1}{2}.\frac{{\pi}k}{n})}.\sqrt{2}=r.\sin{(\frac{\pi}{2n}.\lfloor\frac{n}{2}\rfloor)}.\sqrt{2}$↵
↵
$u=r.\sin{(\frac{1}{2}.\frac{\pi(n-k)}{n})}.\sqrt{2}$↵
↵
$ans=v+u$↵
↵
For [Educational Codeforces Round 87](https://codeforces.net/contest/1354) [C2](https://codeforces.net/contest/1354/problem/C2):↵
↵
```c++↵
double r = 1.0/(2.0*sin(PI/(2*n)));↵
double v = r*sin(PI/(2*n)*(n/2))*sqrt(2);↵
double u = r*sin(PI/(2*n)*(n-n/2))*sqrt(2);↵
double ans = v + u;↵
```↵
↵
We can further simplify $v+u$:↵
↵
$v=r\sqrt{2}\sin{(\frac{\pi}{2n}.\frac{n-1}{2})}$↵
↵
$u=r\sqrt{2}\sin{(\frac{\pi}{2n}.(n-\frac{n-1}{2}))}$↵
↵
$ans=v+u=r\sqrt{2}[\sin{(\frac{\pi}{4}-\frac{\pi}{4n})}+\sin{(\frac{\pi}{4}+\frac{\pi}{4n})}]=\frac{\sqrt{2}}{2\sin{\frac{\theta}{2}}}.2\sin{\frac{\pi}{4}}\cos{\frac{-\pi}{4n}}$↵
↵
$\implies ans=\frac{s.\cos{\frac{\pi}{4n}}}{\sin{\frac{\pi}{2n}}}$↵
↵
As a solution to [1354C2](https://codeforces.net/contest/1354/problem/C2):↵
↵
```c++↵
double ans = cos(PI/(4*n))/(sin(PI/(2*n)));↵
```↵
↵
All figures above (except the 1st figure) were drawn in [GeoGebra Geometry](https://www.geogebra.org/geometry). Additionally, [GeoGebra](https://www.geogebra.org/) is a a free dynamic mathematics software containing several apps:↵
↵
- Graphing calculator↵
↵
- Geometry↵
↵
- 3D Calculator↵
↵
- CAS Calculator↵
↵
- Scientific Calculator↵





