I encountered a problem about probability in a local contest but cannot figure out how to solve it.
Here is the problem statement (since they have removed the online pdf file):
There are N inclusive ranges $$$[a_i, b_i]$$$, i=1, 2, 3, ... N. Now for every range choose a random real number, find the probability that the range i gives the highest result. In case there are two or more highest results, there is no winner.
Constraints: $$$1<=N<=300$$$, $$$0<=a_i, b_i<=1e9$$$
Up until now, my thinking goes like this: I will compose a set of non-intersecting smaller ranges such that for every i the range $$$[a_i, b_i]$$$ can be formed by combining some ranges in the set.
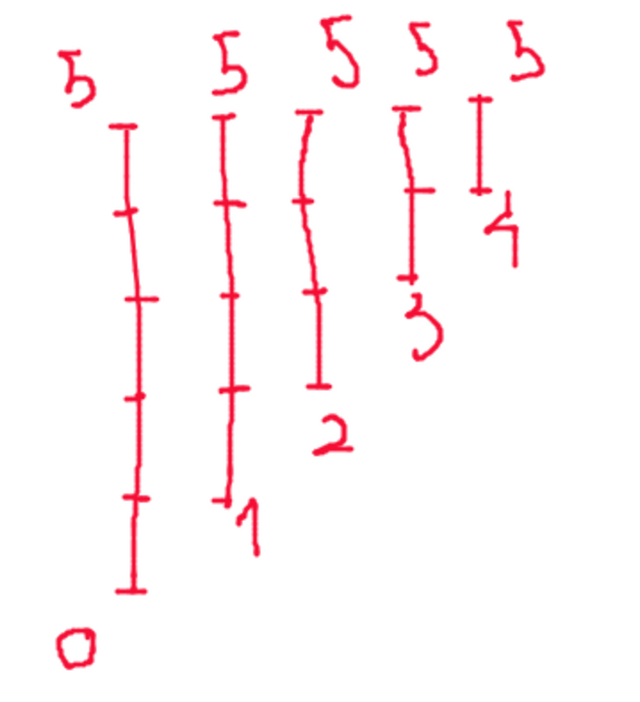
For example the test: N = 5; [0, 5]; [1, 5]; [2, 5]; [3, 5]; [4, 5];
The set is: S = {[0, 1], [1, 2], [2, 3], [3, 4], [4, 5]}
Some visual:
There is around O(N) ranges in this set. The for every i, I will check the probability of it winning if the number chosen is from some range in S. For example, in the above test, I will find the probability of 1 winning by considering if the number is chosen from [0,1], [1, 2]... seperately. Then find the answer for i by summing them up. This solution is O(N^3).
However this is where I have got a Wrong Answer doing it on paper. Maybe I have some mistakes using the calculus,
Anyone please help me with this problem. Thanks in advance.