Hello, Codeforces!

This blog is heavily inspired by TLE's blog using merging segment tree to solve problems about sorted list. I don't know exactly how well known this data structure is, but I thought it would be nice to share it anyway, along with some more operations that are possible with it.

What it can do

We want a data structure that we can think of a set/multiset of non-negative integers, or even as a sorted array. We want to support all of the following operations:

1. Create an empty structure;
2. Insert an element to the structure;
3. Remove an element from the structure;
4. Print the $$$k$$$'th smallest element (if we think of the structure as a sorted array $$$a$$$, we are asking for $$$a[k]$$$);
5. Print how many numbers less than $$$x$$$ there are in the set (similar to lower_bound in a std::vector);
6. Split the structure into two: one containing the $$$k$$$ smallest elements, and the other containing the rest;
7. Merge two structures into one (no extra conditions required).

Turns out that, if all elements are not greater than $$$N$$$, we can perform any sequence of $$$t$$$ such operations in $$$\mathcal{O}(t \log N)$$$, meaning that each operation costs $$$\mathcal{O}(\log N)$$$ amortized (as we will see, all operations except for (7) have worst case $$$\mathcal{O}(\log N)$$$).

How it works

We are going to use a dynamic segment tree to represent the elements. Think of each of them as an index, a leaf on a segment tree. We want the segment tree do be dynamic (we only create the nodes when we need them).

So, initially, there are no nodes on the structure (grey nodes are not present in the structure):

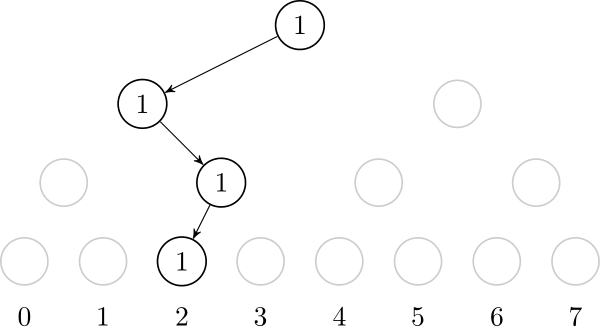
If we insert the value $$$2$$$, we need to create the path from the root to the leaf that represents $$$2$$$. It is also useful to store, on each node, the number of created leafs on that node's subtree.

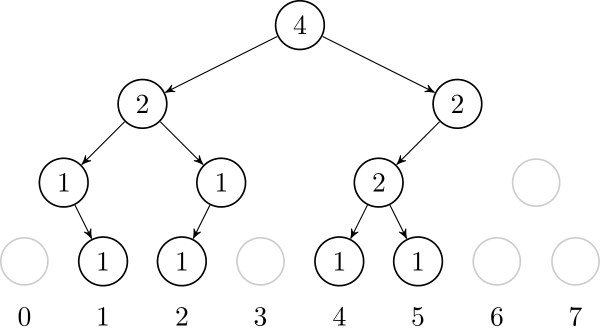
Let's also add $$$1$$$, $$$4$$$ and $$$5$$$. In the end, the tree will look like this:

Using this representation, it is very straightforward to implement operations (1), (2) and (3). Operations (4) and (5) are also easy, they are classic segtree operations. To do operation (6), we can go down the tree and either call recursively to the left or right child. Here is a pseudocode of this operation:

node* split(node*& i, int k) {
    if (!k or !i) return NULL;
    node* ret = new node();
    if (i is a leaf) {
        i->cnt -= k; // assuming multiset
        ret->cnt += k;
    } else {
        if (k <= i->left->cnt) ret->left = split(i->left, k); // split the left
        else { // take everything from the left and split the right
            ret->left = i->left;
            ret->right = split(i->right, k - i->left->cnt);
            i->left = NULL;
        }
    }
    return ret;
}

It is clear that all these operations cost $$$\mathcal{O}(\log N)$$$. On operation (6), note that we only go down recursively to the left or to the right child.

But what about operation (7)? It turns out that we can merge two structures in the following way: to merge the subtrees defined by nodes l and r, if one of them is empty, just return the other. Otherwise, recursively merge l->left and r->left, and l->right and r->right. After that, we can delete either l or r, because they are now redundant: we only need one of them.

Now let's see why any sequence of $$$t$$$ operations will take $$$\mathcal{O}(t \log N)$$$ time. The number of nodes we create is bounded by $$$\mathcal{O}(t \log N)$$$, because each operation creates at most $$$\mathcal{O}(\log N)$$$ nodes. Now note that the merge algorithm either returns in $$$\mathcal{O}(1)$$$, or it deletes one node. So total number of times the algorithm doesn't return in $$$\mathcal{O}(1)$$$ is bounded by the total number of created nodes, so it is $$$\mathcal{O}(t \log N)$$$.

Implementation

There are some implementation tricks that make the code easier to write and use. Firstly, we don't need to set $$$N$$$ as a constant. Instead, we can have $$$N = 2^k-1$$$ for some $$$k$$$, and if we want to insert an element larger than $$$N$$$, we can just increase $$$k$$$, and update the segment tree (we will only need to create a new root, and set its left child to the old root).

Also, it's easy to change between set and multiset representation. It is also easy to insert $$$x$$$ occurrences of an element at once, just increase the cnt variable of the respective leaf accordingly.

This implementation uses $$$\mathcal{O}(t \log N)$$$ of memory, for $$$t$$$ operations.

template<typename T, bool MULTI=false, typename SIZE_T=int> struct sms {
	struct node {
		node *l, *r; // left and right childs
		SIZE_T cnt; // subtree leaf count
		node() : l(NULL), r(NULL), cnt(0) {}
		void update() { // update subtree leaf count
			cnt = 0;
			if (l) cnt += l->cnt;
			if (r) cnt += r->cnt;
		}
	};

	node* root;
	T N;

	sms() : root(NULL), N(0) {}
	sms(T v) : sms() { while (v >= N) N = 2*N+1; }
	sms(const sms& t) : root(NULL), N(t.N) { // copy - O(t log(N))
		for (SIZE_T i = 0; i < t.size(); i++) {
			T at = t[i];
			SIZE_T qt = t.count(at);
			insert(at, qt);
			i += qt-1;
		}
	}
	sms(initializer_list<T> v) : sms() { for (T i : v) insert(i); }
	~sms() {
		vector<node*> q = {root};
		while (q.size()) {
			node* x = q.back(); q.pop_back();
			if (!x) continue;
			q.push_back(x->l), q.push_back(x->r);
			delete x;
		}
	}

	friend void swap(sms& a, sms& b) { // O(1) swap
		swap(a.root, b.root), swap(a.N, b.N);
	}
	SIZE_T size() const { return root ? root->cnt : 0; }
	SIZE_T count(node* x) const { return x ? x->cnt : 0; }
	void clear() {
		sms tmp;
		swap(*this, tmp);
	}
	void expand(T v) { // increase N so value 'v' will fit
		for (; N < v; N = 2*N+1) if (root) {
			node* nroot = new node();
			nroot->l = root;
			root = nroot;
			root->update();
		}
	}

	node* insert(node* at, T idx, SIZE_T qt, T l, T r) {
		if (!at) at = new node();
		if (l == r) {
			at->cnt += qt;
			if (!MULTI) at->cnt = 1;
			return at;
		}
		T m = l + (r-l)/2;
		if (idx <= m) at->l = insert(at->l, idx, qt, l, m);
		else at->r = insert(at->r, idx, qt, m+1, r);
		return at->update(), at;
	}
	void insert(T v, SIZE_T qt=1) { // insert 'qt' occurrences of 'v'
		if (qt <= 0) return erase(v, -qt);
		assert(v >= 0);
		expand(v);
		root = insert(root, v, qt, 0, N);
	}

	node* erase(node* at, T idx, SIZE_T qt, T l, T r) {
		if (!at) return at;
		if (l == r) at->cnt = at->cnt < qt ? 0 : at->cnt - qt;
		else {
			T m = l + (r-l)/2;
			if (idx <= m) at->l = erase(at->l, idx, qt, l, m);
			else at->r = erase(at->r, idx, qt, m+1, r);
			at->update();
		}
		if (!at->cnt) delete at, at = NULL; // 'cnt' is always positive
		return at;
	}
	void erase(T v, SIZE_T qt=1) { // erase 'qt' occurrences of 'v'
		if (v < 0 or v > N or !qt) return;
		if (qt < 0) insert(v, -qt);
		root = erase(root, v, qt, 0, N);
	}
	void erase_all(T v) { // remove all occurrences of 'v'
		if (v < 0 or v > N) return;
		root = erase(root, v, numeric_limits<SIZE_T>::max(), 0, N);
	}

	SIZE_T count(node* at, T a, T b, T l, T r) const {
		if (!at or b < l or r < a) return 0;
		if (a <= l and r <= b) return at->cnt;
		T m = l + (r-l)/2;
		return count(at->l, a, b, l, m) + count(at->r, a, b, m+1, r);
	}
	SIZE_T count(T v) const { return count(root, v, v, 0, N); }
	SIZE_T order_of_key(T v) { return count(root, 0, v-1, 0, N); }
	SIZE_T lower_bound(T v) { return order_of_key(v); }

	const T operator [](SIZE_T i) const { // i-th smallest element (0 -> smallest)
		assert(i >= 0 and i < size());
		node* at = root;
		T l = 0, r = N;
		while (l < r) {
			T m = l + (r-l)/2;
			if (count(at->l) > i) at = at->l, r = m;
			else {
				i -= count(at->l);
				at = at->r; l = m+1;
			}
		}
		return l;
	}

	node* merge(node* l, node* r) {
		if (!l or !r) return l ? l : r;
		if (!l->l and !l->r) { // 'l' is a leaf
			if (MULTI) l->cnt += r->cnt;
			delete r;
			return l;
		}
		l->l = merge(l->l, r->l), l->r = merge(l->r, r->r);
		l->update(), delete r;
		return l;
	}
	void merge(sms& s) { // merge two sets
		if (N > s.N) swap(*this, s);
		expand(s.N);
		root = merge(root, s.root);
		s.root = NULL;
	}

	node* split(node*& x, SIZE_T k) {
		if (k <= 0 or !x) return NULL;
		node* ret = new node();
		if (!x->l and !x->r) x->cnt -= k, ret->cnt += k;
		else {
			if (k <= count(x->l)) ret->l = split(x->l, k);
			else {
				ret->r = split(x->r, k - count(x->l));
				swap(x->l, ret->l);
			}
			ret->update(), x->update();
		}
		if (!x->cnt) delete x, x = NULL; // 'cnt' is always positive
		return ret;
	}
	void split(SIZE_T k, sms& s) { // get the 'k' smallest elements
		s.clear();
		s.root = split(root, min(k, size()));
		s.N = N;
	}
	// get all elements smaller than 'k'
	void split_val(T k, sms& s) { split(order_of_key(k), s); }
};

sms<int> s; // set
sms<int, true> s; // multiset
sms<int, true, long long> s; // multiset, if you want to insert more than 1e9 elements

sms<int, true> s; // multiset
s.insert(3); // insert value '3'
s.insert(4, 3); // insert value '4' three times
s.erase(4); // erase one occurrence of value '4'
s.erase(3, 5); // erase 5 occurrences of value '3'
s.erase_all(4); // erase all occurrences of value '4'

sms<int, true> s = {4, 7, 3, 4, 1, 6, 3}; // now s = {1, 3, 3, 4, 4, 6, 7}
cout << s.order_of_key(4) << endl; // prints "3"
cout << s[0] << " " << s[3] << " " << s[5] << endl; // prints "1 4 6"

sms<int, true> s = {1, 3, 3, 4, 4, 6, 7};
sms<int, true> s2;
s.split(4, s2); // get the 4 smallest elements from s
// now s = {4, 6, 7} and s2 = {1, 3, 3, 4}

sms<int, true> s3 = {2, 4, 6};
s3.merge(s2);
// now s3 = {1, 2, 3, 3, 4, 4, 6}

Memory optimization

Another way to think about this data structure is as a trie. If we want to insert numbers 1, 2, 4, and 5, we can think of them as 001, 010, 100, and 101. After inserting them, it will look like this:

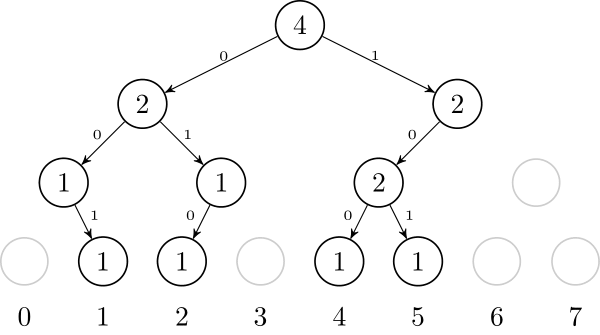
Using this idea, it is possible to represent this trie in a compressed form, just like a Patricia Trie or Radix Trie: we only need to store the non-leaf nodes that have 2 children. So, we only need to store nodes that are LCA of some pair of leafs. If we have $$$t$$$ leafs, that is $$$2t-1$$$ nodes.

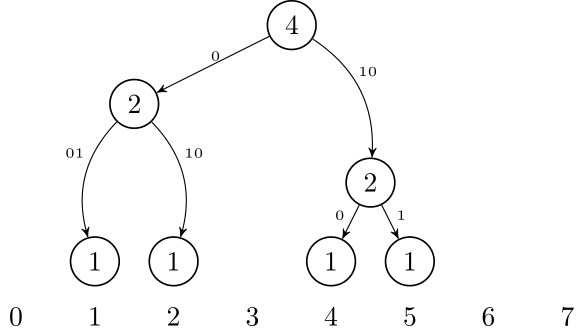
This is very tricky to implement, but it can reduce the memory usage from $$$\mathcal{O}(t \log N)$$$ to $$$\mathcal{O}(t)$$$.

Extra operations

There are some more operations you can do with this data structure. Some of them are:

1. Insert an arbitrary number of occurrences of the same element;
2. You can modify it to use it as a map from int to something, and also have a rule of merging two mappings (for example, if in set $$$A$$$ $$$x$$$ maps to $$$u$$$ and in set $$$B$$$ $$$x$$$ maps to $$$v$$$, it can be made so that in the merged set $$$x$$$ maps to $$$u \cdot v$$$);
3. Using lazy propagation and possibly modifying the merge function, it is possible to do operations like insert a range of values (insert values $$$a, a+1, a+2, \dots b$$$ all at once), or flip a range of values (for every $$$x \in [a, b]$$$, if it is in the set, remove it, otherwise insert it), etc, maintaining the complexity of all operations;
4. I haven't implemented this, but it should be possible to use an implicit treap (or other balanced binary search tree) to represent an array, so that in each node of the treap you store a sorted subarray represented by this structure. Using this, we can do all of the usual operations of implicit tree such as split, concatenate, reverse, etc (but not lazy updates); however we can also sort a subarray (increasing or decreasing). To sort a subarray, just split the subarray into a treap and merge all of the subarray structures. Amortized time complexity should be $$$\mathcal{O}(\log n + \log N)$$$ for $$$t$$$ operations on an array of size $$$n$$$.

Downsides

The memory consumption of the data structure might be a problem, though it can be solved with a more complicated code. The code is already not small at all. Another big downside is the amortized complexity, which leaves us with almost no hope to do rollbacks or to have this structure persistent. Also, the constant factor seems to be quite big, so the structure is not so fast.

Final remarks

The core of the idea was already explained on TLE's blog, and I also found this paper which describes its use as a dictionary (map). Furthermore, while I was writing this, bicsi posted a very cool blog where he shows an easier way to have the memory optimization, but it seems to make the split operation more complicated.

Problems

Using this structure to solve these problems is an overkill, but they are the only examples I got.

• 911G - Mass Change Queries

• 558E - A Simple Task