Introduction
Summary
How to determine the analytical formula? The original undetermined coefficient method not only has small scalability, but also has a large amount of calculation, and it performs poorly in computer science design operations. The Lagrangian interpolation method can solve this problem. This article first introduces the Lagrangian interpolation method, and explores the process of using the Lagrange interpolation method to solve the problem. It discusses the application of Lagrangian interpolation in the four aspects of basic function properties, factorization, proof of algebraic identities, and finding the relationship between the serial numbers and numerical values of several ordered and regular numbers.
Symbol Convention
$$$\prod$$$ means accumulative multiplication operation, generally its subscript will be used as the condition of accumulative multiplication;
$$$\sum\limits^n_{i=1}i$$$ means $$$1+2+3+\cdots+n$$$;
$$$f(k)$$$ represents the value of the function of $$$x$$$ when $$$x=k$$$;
- $$$y=f(x)$$$ means that $$$y$$$ is a function of $$$x$$$.
Source of the problem
In class, the teacher talked about using the method of undetermined coefficients to find the analytical formula of a function. If it is a linear function, set it to the form of $$$f(x)=y=kx+b$$$, and the result can be obtained after substituting two sets of values. For higher power functions, the undetermined coefficient method is also feasible, but the increase in the number of elements in the solution equations makes the undetermined coefficient method lose its original simplicity. Therefore, we will discuss how to determine the analytical expression of a function in combination with polynomials. Let's first study how many points on the graph of a given function, we can determine a unique function. The functions explored here are all polynomial functions, that is, the functions are polynomials.
Lemma
$$$n+1$$$ points determine a polynomial function of degree $$$n$$$.
Proof
We consider the most primitive method of undetermined coefficients. Suppose a polynomial function of degree $$$n$$$ $$$y=f(x)=\sum\limits_{i=0}^na_ix^i$$$ is the required function, and we finally have the sum in the equation system composed of the undetermined coefficient method A system of equations with the same number of a$. Therefore, it takes $$$n+1$$$ equations to solve all $$$a$$$.
Then we will give $$$n$$$ points below and ask to determine a polynomial function of degree $$$n-1$$$.
Questions raised
Given $$$n$$$ points on the function graph $$$P_i(x_i,y_i)(i=1,2,\cdots,n)$$$, at most $$$n-1$$$ degree polynomials passing through these $$$n$$$ points The function is set to $$$y=f(x)=\sum\limits_{i=0}^{n-1}a_ix^i$$$, and find: (1) When $$$x=k$$$, the value of $$$y$$$; (2) Find the function expression of $$$y$$$ and $$$x$$$.
Problem solving
The undetermined coefficient method is indeed a method, but it is too cumbersome. Even if it is solved in a computer, the asymptotic function of the time complexity is $$$\Theta(n^3)$$$, which is not efficient. So, is there a more efficient method? Below we introduce Lagrangian interpolation and its application.
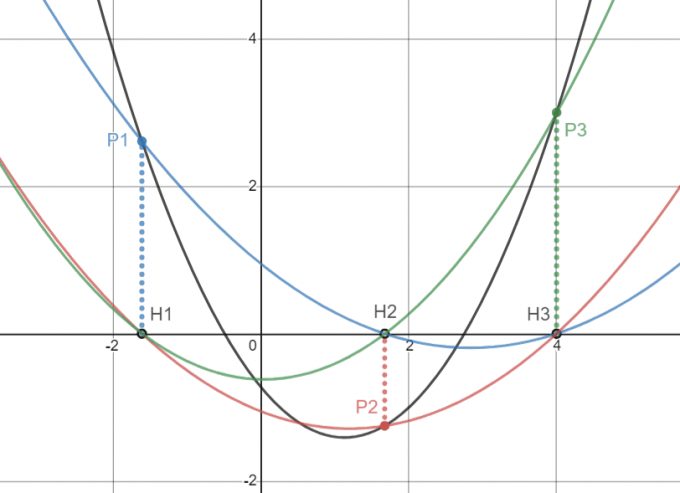
Suppose $$$y$$$ is the required function of $$$x$$$ (its image is represented by a black line), and we use $$$P_i(x_i,y_i)$$$ to make the perpendicular line of the $$$x$$$ axis intersect the $$$x$$$ axis at $$$H_i(x_i, 0)$$$, for each $$$i$$$, construct the following function $$$g_i(x)$$$ (the image is represented by a colored line) so that its image passes through all the points $$$H$$$ except $$$H_i$$$ and passes Click $$$P_i$$$.
If we consider describing such a function, we can find that the value of the function $$$g_i(x)$$$ at $$$x_i$$$ is $$$g_i(x_i)=y_i$$$, and the other values at $$$x_j(i\neq j)$$$ $$$g_i(x_j)=0$$$, so we can define the function $$$g_i(x)$$$ like this:
It is easy to construct its analytical formula
among them
It is called the interpolation basis function, which satisfies $$$\ell_i(x_i)=1$$$, $$$\ell_i(x_j)(i\neq j)=0$$$.
Theorem
The final function $$$y=f(x)=\sum\limits_{i=0}^{n-1}a_ix^i$$$ is the sum of all $$$g_i(x)$$$. Formally,
Proof
Since the image of $$$g_i(x)$$$ passes $$$P_i$$$, and the others pass $$$H_j(i\neq j)$$$, the function image of the sum of all $$$z_i$$$ must pass all $$$P_i$$$, and the final function is determined .
In the process of solving the above problems, we also got the Lagrangian formula, that is, the Lagrangian interpolation method is used to express the form of the function. This will be very common in the following applications. It is also a common method to prove algebraic identities by comparing the coefficients of the same term in different representations of functions (using Lagrange formula here).
Lagrange formula
That is the $$$(*)$$$ formula.
Description
All of the above $$$i,j=1,2,\cdots,n$$$ and $$$i\neq j$$$.
Lagrangian interpolation and the application of Lagrangian formula
We can extend Lagrangian interpolation to other mathematical applications, so that it is not only used to find functional analytical expressions. For example, the following factorization problem:
Example
Decompose the factor $$$a^2(m-b)(m-c)(c-b)+b^2(m-c)(m-a)(a-c)+c^2(m-a)(m-b)(b-a)$$$.
Analysis
Observe the form of factorization and find that it is a bit like the form on the right side of the Lagrangian formula of $$$f(x)=x^2$$$. Consider using the Lagrangian formula.
Answer
Note that by the Lagrangian interpolation method, let $$$a, b, c$$$ be the abscissa of a given point $$$x_1, x_2, x_3$$$, then the ordinate of the given point $$$y_1, y_2, y_3$$$ is $$$f( a),f(b),f(c)$$$, $$$y=f(x)=x^2$$$ are the functions on the left side of the Lagrange formula, then
So there is
In the above formula, let $$$x=m$$$ to get
The following is an example of using the Lagrange formula to prove the effect of algebraic identities by comparing the coefficients of a certain term.
Example
(Olympic classics and algebra problems in Olympic mathematics) $$$^2$$$ Let $$$a,b,c$$$ be the three sides of non-isosceles $$$\triangle ABC$$$, and $$$S$$$ is the area, verify: $$$\dfrac{a^3}{(a-b)(a-c)}+\dfrac{b^3}{(b-c)(b-a)}+\dfrac{c^3}{(c-a)(c-b)}>2\times \sqrt{\sqrt{3}^3}\sqrt{S}$$$.
Analysis
First deal with the denominators of the fractions on the left side of the inequality, and observe that it is in the form of an interpolation basis function, so we can construct a function so that the elements on the right side of the Lagrangian formula are the content on the left side of the inequality sign, so we consider constructing a quadratic function . Furthermore, it can be found that the coefficient of $$$x^2$$$ in the Lagrangian interpolation representation of the quadratic function $$$y=f(x)=x^3-(x-a)(x-b)(x-c)$$$ is exactly on the left side of the inequality sign Formula, which is equal to $$$a+b+c$$$, so the Helen formula is considered. The result can be obtained by using Helen's formula.
Proof
Consider the following function $$$y=f(x)=x^3-(x-a)(x-b)(x-c)$$$, consider setting $$$a,b,c$$$ as the abscissa of a given point $$$x_1,x_2,x_3$$$ , The ordinate $$$y_1, y_2, y_3$$$ of the given point are respectively $$$a^3, b^3, c^3$$$. Consider the Lagrangian representation of the function, that is, the sum of all the above $$$g_i(x)$$$, we can get
Compare the coefficient of $$$x^2$$$ to get
So the original question is transformed into proof $$$a+b+c<2\times \sqrt{\sqrt{3}^3}\sqrt{S}$$$. The following is a geometric problem, the proof is omitted.
The following is an example of using the Lagrangian formula to find the formula of $$$a_i$$$ for any $$$n$$$ given $$$a_i$$$.
Example
Given that $$$a_1=14,a_2=58,a_3=166,a_4=368$$$, for $$$n=1,2,3,4$$$, try the polynomial with the highest degree of 3 containing $$$n$$$ to express $$$a_n$$$ .
Answer
Consider setting the general term formula as $$$a_n=f(n)$$$, then $$$f(1)=14, f(2)=58, f(3)=166, f(4)=368$$$.
The following regards $$$1,2,3,4$$$ as the abscissa of a given point $$$x_1,\dots,x_4$$$, and $$$14,58,166,368$$$ as the ordinate of a given point $$$y_1,\cdots,y_4$$$, then
The following example is about discussing the range of a certain point value of a polynomial.
Example
Given the function $$$f(x)=x^3+px^2+qx+r$$$, where $$$p,q,r$$$ are real numbers. Proof: One of the $$$|f(1)|,|f(2)|,|f(3)|,|f(4)|$$$ must be no less than $$$\dfrac{3}{4}$$$.
Analysis
Consider the Lagrangian formula of the polynomial function, take $$$x_1, x_2, x_3, x_4$$$ as $$$1,2,3,4$$$ respectively; take $$$y_1, y_2, y_3, y_4$$$ respectively to the value of the corresponding function, and finally Then consider the coefficient of $$$x^3$$$.
Proof
Take $$$x_1,x_2,x_3,x_4$$$ as $$$1,2,3,4$$$ respectively; take $$$y_1,y_2,y_3,y_4$$$ respectively as the value of the corresponding function, which is obtained by Lagrangian formula
Comparing the coefficients around $$$x^3$$$ in the above formula, we can get
So
The following example is still about the range of a point value of the polynomial.
Example
The known function $$$f(x)=ax^3+bx^2+cx+d$$$, if $$$p\leq f(-1)\leq q,p\leq f(1)\leq r,q\leq f(2)\leq s,t\leq f(3)\leq p$$$, use $$$p,q,r,s,t$$$ to denote the value range of $$$f(4)$$$.
Analysis
Considering that for the cubic polynomial function, $$$4$$$ corresponding value ranges are given, and the conditions required for Lagrangian interpolation are met, you can take $$$x_1=-1,x_2=1,x_3=2,x_4=3$$$ , So we can use Lagrangian interpolation to express $$$f(4)$$$ (see the question), and then according to the value range of the four function values, we can get that when $$$x=4$$$, The value range of $$$y$$$.
Answer
Take $$$x_i=-1,1,2,3$$$, which can be obtained by Lagrangian formula
So $$$\dfrac{9}{4}p-5q+\dfrac{5}{4}t\leq f(4)\leq -\dfrac{1}{4}q+\dfrac{5}{2}r- 5s+\dfrac{5}{4}p$$$.
References
[1] OI Wiki. Lagrangian interpolation [EB/OL].
[2] Shen Wenxuan, Zhang Yao, Leng Gangsong. Olympiad Classics · Algebraic Problems in Olympic Mathematics [M]. Changsha: Hunan Normal University Press, 2009.5: 322.
If you have some more applications of the Lagrange Interpolation in Informatics or Mathematics, please comment here and make this post better.
Thanks to ghoshsai5000 for the two sample questions!