**I thought the explanations which I came up for Yestersday's A,C and E were easier to understand. So here they are.**↵
A↵
==================↵
### hint↵
Try making solution of n=4 or n=5↵
### solution↵
Handle $n=1$ ,$n=2$ and $n=3$ case separately↵
Now $n>=4$ the answer will always have 9 in first position.Solution depends only on the first position at which we stopped.Suppose we stop at position $p>=3$.↵
↵
If 1st position is stopped at timet1$t_1$, then second position must have stopped at time t$t_2=t_1-1$, third at t$t_3 = t_2-1 = t_1-2$↵
Since first position have 9 and second is stopped at a second earlier second position is 8 and similarly third position is 7.↵
↵
If u have tried building solution for n=4 you must have observed that it is possible to 989 in first three positions respectively which better solution than the one we tried to construct above. Thus stopping at 2nd position when it shows 8 is optimal solution.↵
↵
To construct rest of the string ↵
s[I]=(s[I-1]+1)%10↵
### code↵
↵
~~~~~↵
#include<iostream>↵
using namespace std;↵
int main(){↵
int te;cin>>te;↵
while(te--){↵
int n;cin>>n;↵
if(n==1){cout<<"9\n";continue;}↵
if(n==2){cout<<"98\n";continue;}↵
if(n==3){cout<<"989\n";continue;}↵
int ans[n];↵
ans[0]=9;↵
ans[1]=8;↵
ans[2]=9;↵
for(int i=3;i<n;i++)ans[i]=(ans[i-1]+1)%10;↵
for(int i=0;i<n;i++)cout<<ans[i];↵
cout<<endl;↵
}↵
}↵
~~~~~↵
↵
↵
C↵
==================↵
### hint↵
We are first trying to create a max negative value which we will then in final step subtract from a positive value↵
### solution↵
Suppose the bags are↵
A$a_1,a_2,a_3……an1_{n_1}$<Br>↵
B$b_1,b_2,b_3…..Bn2b_{n_2}$<Br>↵
C$c_1,c_2,c_3……cn3_{n_3}$<Br>↵
Let**sum**$SUM=a_1+a_2+a_3….+an1_{n_1}+b_1+b_2+b_3….-bn2+b_{n_2}+c_1+c_2+c_3….+cn3_{n_3}$<Br>↵
We can have mainly have two type of final values<br>↵
↵
**First**↵
We can subtract valuesb$b_2,b_3,b_4…..bn2_{n_2}, c_1,c_2,c_3……cn3_{n_3}$ from an1$a_1$<Br> ↵
The value ofa1$a_1$ would then be a$a_1-b_2-b_3-b_4…..bn2_{n_2}-c_1-c_2-c_3…..-cn3_{n_3}$<Br>↵
And then finally subtracta$a_1,a_2,a_3…..an1_{n_1}$ from b1$b_1$<Br>↵
The value ofb1$b_1$ would then be<Br>↵
b$b_1-(a_1-b_2-b_3-b_4…..bn2_{n_2}-c_1-c_2-c_3…..-cn3_{n_3})-a_2-a_3-a_4…an1_{n_1}$<Br>↵
$=b_1+b_2+b_3….Bn1b_{n_1}+c_1+c_2+c_3…..+cn3_{n_3}-a_1-a_2-a_3-a_4…an1_{n_1}$<Br>↵
$=sum-2*(a_1+a_2+a_3….An1)a_{n_1})$<Br>↵
↵
**Second**↵
Another answer that we can construct is<Br>↵
Subtract valuesb$b_2,b_3,b_4…..bn2_{n_2}, c_2,c_3……cn3_{n_3}$ from an1$a_1$ <br> **NOTE we are not subtracting c1$c_1$**<Br>↵
The value ofa1$a_1$ will be a$a_1-b_2-b_3-b_4…..bn2_{n_2}-c_2-c_3…..-cn3_{n_3}$<Br>↵
Subtract valuesa$a_2,a_3…..an1_{n_1}$ from cn1$c_1$<Br>↵
The value ofc1$c_1$ will be c$c_1-a_2-a_3-a_4…..an1_{n_1}$<Br>↵
And then finally subtracta1 and c1$a_1$ and $c_1$ from b1$b_1$<Br>↵
The final value would then be<Br>↵
b$b_1-(a_1-b_2-b_3-b_4…..Bn2b_{n_2}-c_2-c_3…..-cn3_{n_3})-(c_1-a_2-a_3-a_4…..an1)_{n_1})$<Br>↵
$=b_1+b_2+b_3….bn2_{n_2}+c_2+c_3+….cn3_{n_3}+a_2+a_3+a_4…an1_{n_1}-a_1-c1_1$<Br>↵
$=sum-2*(a_1+c_1)$<Br>↵
↵
Thus the $answer=max(sum-2*(a_1+a_2+a_3….an1_{n_1}),sum-2*(a_1+c_1))$<Br>↵
$Answer=sum-min(2*(a_1+a_2+a_3….an1_{n_1}),2*(a_1+c_1))$<Br>↵
$Ans=sum-2*min((a_1+a_2+a_3….an1_{n_1}),a_1+c_1)$<Br>↵
I have considered bags randomly without loss of generality <Br>↵
That mean I want to compare the bag which has minimum and sum of minimum elements of any two bags↵
### code↵
↵
~~~~~↵
#include<iostream>↵
#include<bits/stdc++.h>↵
using namespace std;↵
int main(){↵
int n1,n2,n3;↵
cin>>n1>>n2>>n3;↵
long long a[n1], b[n2], c[n3];↵
long long sum=0,sum_of_a=0,sum_of_b=0,sum_of_c=0;↵
long long min_elements[3]={(long long)1e9+3,(long long)1e9+3,(long long)1e9+3};↵
// 0 1 2 stores min elements of bag a b and c respectively↵
↵
for(int i=0;i<n1;i++){cin>>a[i];sum+=a[i];sum_of_a+=a[i];min_elements[0]=min(min_elements[0],a[i]);}↵
for(int i=0;i<n2;i++){cin>>b[i];sum+=b[i];sum_of_b+=b[i];min_elements[1]=min(min_elements[1],b[i]);}↵
for(int i=0;i<n3;i++){cin>>c[i];sum+=c[i];sum_of_c+=c[i];min_elements[2]=min(min_elements[2],c[i]);}↵
sort(min_elements,min_elements+3);↵
long long min_sum_bag=min(sum_of_a,sum_of_b);↵
min_sum_bag=min(min_sum_bag,sum_of_c);↵
sum-=2*min(min_elements[0]+min_elements[1],min_sum_bag);↵
cout<<sum<<endl;↵
}↵
~~~~~↵
↵
↵
↵
E↵
### Solution↵
Let us see when the answer is definitely 0<br>↵
Suppose three vertices x,y,z exists such that ax=ay=az and y lies on path from x to z (or z=x since undirected tree both are same)<br>↵
In this scenario the answer is always 0.<br>↵
This can be understood by the given image (I was not write the formal proof)<br>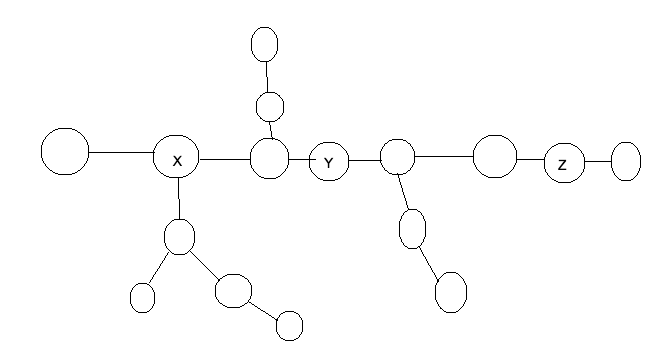<br>↵
Try getting a distinctive root in this tree<br>↵
After checking the above case we can simply iterate over nodes in any order.<br>↵
Suppose we are node **v**↵
If the value of the node is unique i.e. no other other element has same value as this node we don't need to anything.↵
Otherwise we check which edge of this node leads us to another node having same value.<br>↵
The condition which we checked initially assures that there will be exactly one such edge for each node.<br>↵
Let this edge be **E**.Now all the node which do not contain this edge in their path to **v** cannot be distinctive roots.↵
Once you try few cases of own it easy to understand why.<br>↵
To implement the above solution we can arbitrarily root the tree, do a dfs and assign each vertex a in and out time.↵
Now if we are at vertex **v** and vertex **w** is connected to **v** by an edge **E1!=E** we can cancel off all the vertex in subtree of **v**. To do so we can maintain array **fin** with initial values 0 and reduce all values from in[v] to out[v]+1 time.<br>↵
Now to obtain final answer iterate over all node and if **fin[in[v]]==0** increase answer.↵
### code↵
Don't have clean implementation at the moment. I will write and update if this blog got some likes.↵
A↵
==================↵
### hint↵
Try making solution of n=4 or n=5↵
### solution↵
Handle $n=1$ ,$n=2$ and $n=3$ case separately↵
Now $n>=4$ the answer will always have 9 in first position.Solution depends only on the first position at which we stopped.Suppose we stop at position $p>=3$.↵
↵
If 1st position is stopped at time
Since first position have 9 and second is stopped at a second earlier second position is 8 and similarly third position is 7.↵
↵
If u have tried building solution for n=4 you must have observed that it is possible to 989 in first three positions respectively which better solution than the one we tried to construct above. Thus stopping at 2nd position when it shows 8 is optimal solution.↵
↵
To construct rest of the string ↵
s[I]=(s[I-1]+1)%10↵
### code↵
↵
~~~~~↵
#include<iostream>↵
using namespace std;↵
int main(){↵
int te;cin>>te;↵
while(te--){↵
int n;cin>>n;↵
if(n==1){cout<<"9\n";continue;}↵
if(n==2){cout<<"98\n";continue;}↵
if(n==3){cout<<"989\n";continue;}↵
int ans[n];↵
ans[0]=9;↵
ans[1]=8;↵
ans[2]=9;↵
for(int i=3;i<n;i++)ans[i]=(ans[i-1]+1)%10;↵
for(int i=0;i<n;i++)cout<<ans[i];↵
cout<<endl;↵
}↵
}↵
~~~~~↵
↵
↵
C↵
==================↵
### hint↵
We are first trying to create a max negative value which we will then in final step subtract from a positive value↵
### solution↵
Suppose the bags are↵
Let
We can have mainly have two type of final values<br>↵
↵
**First**↵
We can subtract values
The value of
And then finally subtract
The value of
$=b_1+b_2+b_3….
$=sum-2*(a_1+a_2+a_3….
↵
**Second**↵
Another answer that we can construct is<Br>↵
Subtract values
The value of
Subtract values
The value of
And then finally subtract
The final value would then be<Br>↵
$=b_1+b_2+b_3….b
$=sum-2*(a_1+c_1)$<Br>↵
↵
Thus the $answer=max(sum-2*(a_1+a_2+a_3….a
$Answer=sum-min(2*(a_1+a_2+a_3….a
$Ans=sum-2*min((a_1+a_2+a_3….a
I have considered bags randomly without loss of generality <Br>↵
That mean I want to compare the bag which has minimum and sum of minimum elements of any two bags↵
### code↵
↵
~~~~~↵
#include<iostream>↵
#include<bits/stdc++.h>↵
using namespace std;↵
int main(){↵
int n1,n2,n3;↵
cin>>n1>>n2>>n3;↵
long long a[n1], b[n2], c[n3];↵
long long sum=0,sum_of_a=0,sum_of_b=0,sum_of_c=0;↵
long long min_elements[3]={(long long)1e9+3,(long long)1e9+3,(long long)1e9+3};↵
// 0 1 2 stores min elements of bag a b and c respectively↵
↵
for(int i=0;i<n1;i++){cin>>a[i];sum+=a[i];sum_of_a+=a[i];min_elements[0]=min(min_elements[0],a[i]);}↵
for(int i=0;i<n2;i++){cin>>b[i];sum+=b[i];sum_of_b+=b[i];min_elements[1]=min(min_elements[1],b[i]);}↵
for(int i=0;i<n3;i++){cin>>c[i];sum+=c[i];sum_of_c+=c[i];min_elements[2]=min(min_elements[2],c[i]);}↵
sort(min_elements,min_elements+3);↵
long long min_sum_bag=min(sum_of_a,sum_of_b);↵
min_sum_bag=min(min_sum_bag,sum_of_c);↵
sum-=2*min(min_elements[0]+min_elements[1],min_sum_bag);↵
cout<<sum<<endl;↵
}↵
~~~~~↵
↵
↵
↵
E↵
### Solution↵
Let us see when the answer is definitely 0<br>↵
Suppose three vertices x,y,z exists such that ax=ay=az and y lies on path from x to z (or z=x since undirected tree both are same)<br>↵
In this scenario the answer is always 0.<br>↵
This can be understood by the given image (I was not write the formal proof)<br><br>↵
Try getting a distinctive root in this tree<br>↵
After checking the above case we can simply iterate over nodes in any order.<br>↵
Suppose we are node **v**↵
If the value of the node is unique i.e. no other other element has same value as this node we don't need to anything.↵
Otherwise we check which edge of this node leads us to another node having same value.<br>↵
The condition which we checked initially assures that there will be exactly one such edge for each node.<br>↵
Let this edge be **E**.Now all the node which do not contain this edge in their path to **v** cannot be distinctive roots.↵
Once you try few cases of own it easy to understand why.<br>↵
To implement the above solution we can arbitrarily root the tree, do a dfs and assign each vertex a in and out time.↵
Now if we are at vertex **v** and vertex **w** is connected to **v** by an edge **E1!=E** we can cancel off all the vertex in subtree of **v**. To do so we can maintain array **fin** with initial values 0 and reduce all values from in[v] to out[v]+1 time.<br>↵
Now to obtain final answer iterate over all node and if **fin[in[v]]==0** increase answer.↵
### code↵
Don't have clean implementation at the moment. I will write and update if this blog got some likes.↵





