I thought the explanations which I came up for Yestersday's A,C and E were easier to understand. So here they are.

A

hint

Try making solution of n=4 or n=5

solution

Handle n=1 ,n=2 and n=3 case separately Now n>=4 the answer will always have 9 in first position.Solution depends only on the first position at which we stopped.Suppose we stop at position p>=3.

If 1st position is stopped at time t1, then second position must have stopped at time t2=t1-1, third at t3 = t2-1 = t1-2 Since first position have 9 and second is stopped at a second earlier second position is 8 and similarly third position is 7.

If u have tried building solution for n=4 you must have observed that it is possible to 989 in first three positions respectively which better solution than the one we tried to construct above. Thus stopping at 2nd position when it shows 8 is optimal solution.

To construct rest of the string s[I]=(s[I-1]+1)%10

code

#include<iostream>
using namespace std;
int main(){
    int te;cin>>te;
    while(te--){
        int n;cin>>n;
        if(n==1){cout<<"9\n";continue;}
        if(n==2){cout<<"98\n";continue;}
        if(n==3){cout<<"989\n";continue;}
        int ans[n];
        ans[0]=9;
        ans[1]=8;
        ans[2]=9;
        for(int i=3;i<n;i++)ans[i]=(ans[i-1]+1)%10;
        for(int i=0;i<n;i++)cout<<ans[i];
        cout<<endl;
    }
}

C

hint

We are first trying to create a max negative value which we will then in final step subtract from a positive value

solution

Suppose the bags are A1,a2,a3……an1
B1,b2,b3…..Bn2
C1,c2,c3……cn3
Let sum=a1+a2+a3….+an1+b1+b2+b3….-bn2+c1+c2+c3….+cn3
We can have mainly have two type of final values

First We can subtract values b2,b3,b4…..bn2, c1,c2,c3……cn3 from an1
The value of a1 would then be a1-b2-b3-b4…..bn2-c1-c2-c3…..-cn3
And then finally subtract a1,a2,a3…..an1 from b1
The value of b1 would then be
b1-(a1-b2-b3-b4…..bn2-c1-c2-c3…..-cn3)-a2-a3-a4…an1
=b1+b2+b3….Bn1+c1+c2+c3…..+cn3-a1-a2-a3-a4…an1
=sum-2*(a1+a2+a3….An1)

Second Another answer that we can construct is
Subtract values b2,b3,b4…..bn2, c2,c3……cn3 from an1
NOTE we are not subtracting c1
The value of a1 will be a1-b2-b3-b4…..bn2-c2-c3…..-cn3
Subtract values a2,a3…..an1 from cn1
The value of c1 will be c1-a2-a3-a4…..an1
And then finally subtract a1 and c1 from b1
The final value would then be
b1-(a1-b2-b3-b4…..Bn2-c2-c3…..-cn3)-(c1-a2-a3-a4…..an1)
=b1+b2+b3….bn2+c2+c3+….cn3+a2+a3+a4…an1-a1-c1
=sum-2*(a1+c1)

Thus the answer=max(sum-2*(a1+a2+a3….an1),sum-2*(a1+c1))
Answer=sum-min(2*(a1+a2+a3….an1),2*(a1+c1))
Ans=sum-2*min((a1+a2+a3….an1),a1+c1)
I have considered bags randomly without loss of generality
That mean I want to compare the bag which has minimum and sum of minimum elements of any two bags

code

#include<iostream>
#include<bits/stdc++.h>
using namespace std;
int main(){
int n1,n2,n3;
cin>>n1>>n2>>n3;
long long a[n1], b[n2], c[n3];
long long sum=0,sum_of_a=0,sum_of_b=0,sum_of_c=0;
long long min_elements[3]={(long long)1e9+3,(long long)1e9+3,(long long)1e9+3};
// 0 1 2 stores min elements of bag a b and c respectively

for(int i=0;i<n1;i++){cin>>a[i];sum+=a[i];sum_of_a+=a[i];min_elements[0]=min(min_elements[0],a[i]);}
for(int i=0;i<n2;i++){cin>>b[i];sum+=b[i];sum_of_b+=b[i];min_elements[1]=min(min_elements[1],b[i]);}
for(int i=0;i<n3;i++){cin>>c[i];sum+=c[i];sum_of_c+=c[i];min_elements[2]=min(min_elements[2],c[i]);}
sort(min_elements,min_elements+3);
long long min_sum_bag=min(sum_of_a,sum_of_b);
min_sum_bag=min(min_sum_bag,sum_of_c);
sum-=2*min(min_elements[0]+min_elements[1],min_sum_bag);
cout<<sum<<endl;
}

E

Solution

Let us see when the answer is definitely 0
Suppose three vertices x,y,z exists such that ax=ay=az and y lies on path from x to z (or z=x since undirected tree both are same)
In this scenario the answer is always 0.
This can be understood by the given image (I was not write the formal proof)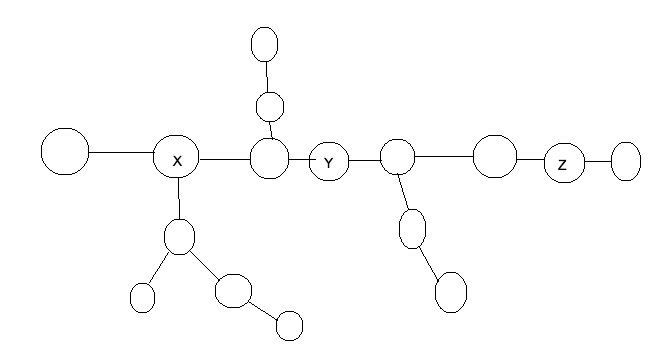

Try getting a distinctive root in this tree
After checking the above case we can simply iterate over nodes in any order.
Suppose we are node v If the value of the node is unique i.e. no other other element has same value as this node we don't need to anything. Otherwise we check which edge of this node leads us to another node having same value.
The condition which we checked initially assures that there will be exactly one such edge for each node.
Let this edge be E.Now all the node which do not contain this edge in their path to v cannot be distinctive roots. Once you try few cases of own it easy to understand why.
To implement the above solution we can arbitrarily root the tree, do a dfs and assign each vertex a in and out time. Now if we are at vertex v and vertex w is connected to v by an edge E1!=E we can cancel off all the vertex in subtree of v. To do so we can maintain array fin with initial values 0 and reduce all values from in[v] to out[v]+1 time.
Now to obtain final answer iterate over all node and if fin[in[v]]==0 increase answer.

code

Don't have clean implementation at the moment. I will write and update if this blog got some likes.