First of all we have to distinguish between two types of an array:
1. Static Array i.e The array values are never updated between the queries
2. Dynamic Array

In range queries our task is to calculate a value based on a subarray of an array.
Types of range queries are:
1. sum(a, b)
2. min(a, b)
3. max(a, b)
Where a, b here stand for the beginning and the ending of the interval

What we're interested in here is the Static Array queries and we will begin with the sum queries

So given an array like this if we want to calculate sum(3, 7)

the first thing may come to your mind is using a loop over this range and we are done. and that's totally fine and the simplest solution the better

int result = 0;
for (int i = 2; i <= 6; i++) {
    result += arr[i];
}

But what if we have a lot of queries ? The running time of the previous naive approach is O(nq) where n is the range length and q is the number of queries.

So before dealing with the queries we will make some preprocessing and construct Prefix Sum Array, And the way to do this is very simple:
1. make an array with size equal to the original array + 1
2. the initial value for the first element is zero Because we need to calculate every cell value using the previous calculated one. and if we used the same array size we will go beyond the array boundary while calculating the first cell.

Then loop through the original array and calculate the prefix sum array as following:
prefix0 = a0
prefix1 = a0 + a1 = a1 + prefix0
prefix2 = a0 + a1 + a2 = a2 + prefix1
....

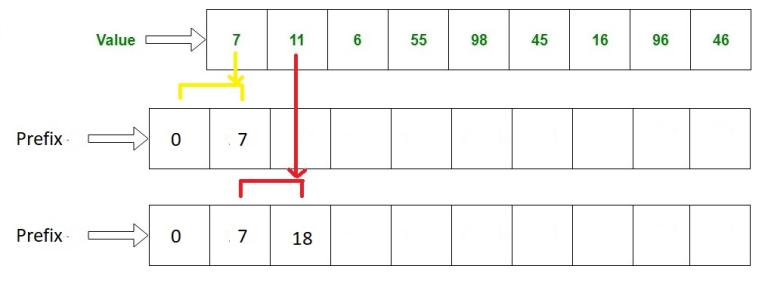
we will end up with something like this:-

As we can see the first cell holds only the first value in the array, the second cell hold the sum of the first two values and the third cell holds the first three values and so on...

Back to the sum query we can now calculate any query in O(1) using this array.
For example: sum(3, 7) is prefix[7] — prefix[2]

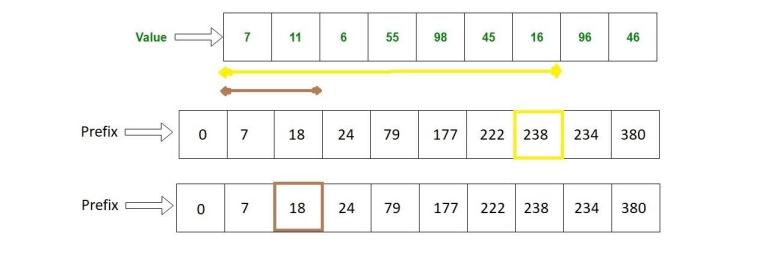
Implementation

int numbers[] = {7, 11, 6, 55, 98, 45, 16, 96, 46};  // length = 9
int prefix[10];
prefix[0] = 0;
for (inti = 1; i < 10; i++)  {
    prefix[i] = prefix[i - 1] + numbers[i - 1];
}