Hello Codeforces!
Today was Codeforces Round #720 (Div.2), in which I solved problem D — Nastia Plays with a Tree. As I find my solution different from the solutions I heard of after the contest, I will explain it in detail in this blog post. I will note that you still might find value in reading this if you solved the problem, as my proposed solution also maintains at every stage the graph being a forest (i.e I don't create any cycles).
I won't use spoiler tags as codeforces ruins them anyways after a few days :/
The Solution
Note that in this editorial, when I write simple path, I mean a simple path between two nodes without having extra edges going from any of the nodes that do not belong to that simple path, or simply a node not connected to anything (this will be clearer once we see drawings).
We should first note that bamboo is simply a tree that looks like a single line of connections (i.e a simple path).
We observe that given the sequence of moves the order we delete/link edges in does not change the resultant underlying graph. We consider the following question: how can we delete edges such that we can link the remaining forest via link operations to make a bamboo after we delete all of them?
Well, we want to achieve a simple path in the end, and a simple path can only be broken into nonintersecting simple paths, therefore after edge deletions, we should have a set of nonintersecting simple paths.
Now, our motivation is to take some pen & paper and draw how such a set looks like (not necessarily the optimal one) (in this editorial I cheat with CSAcademy Graph Editor). **Note that for convenience and as in many tree problems, we root the tree at an arbitrary node.
Suppose we are given the following tree (rooted at node 1): 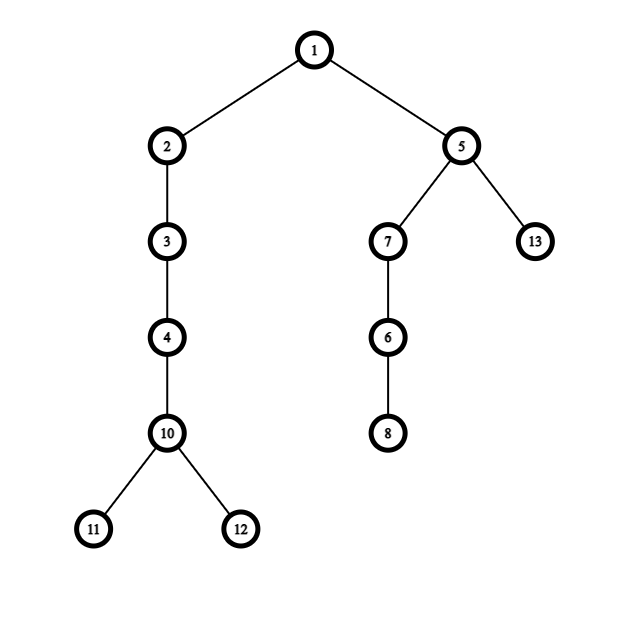
We can convert it to a set of non-intersecting simple paths in multiple ways, one of which is deleting 4->10, 5->13 & 5->7, and if we were to apply this way we would end up with the following set of simple paths: 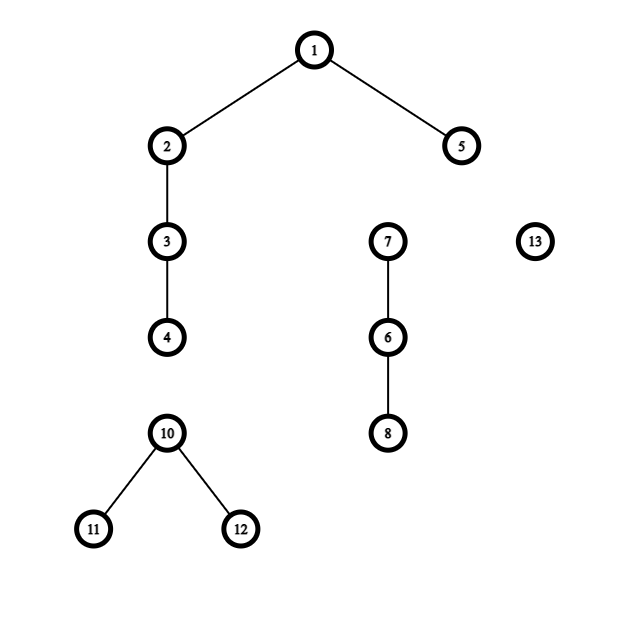
If we look at subtrees of the original tree and what they turned into after the deletion, we observe that if a node has outgoing edges to 2 of its original children from the original subtree then that node must not be connected to its parent.
This leads to an approach of dynamic programming over subtrees & an observation is that we can utilize the following state: whether or not our subtree root is connected to its parent. The motivation for this state is exactly what we state above, in order to connect to more than 1 child we must not be connected to our parent. Let sdp[c] be the minimum






