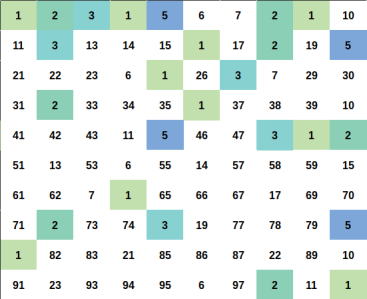
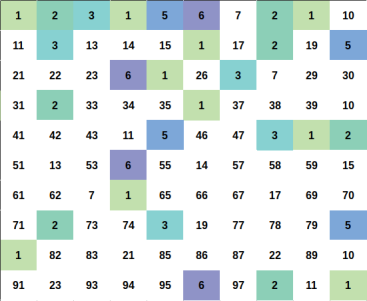
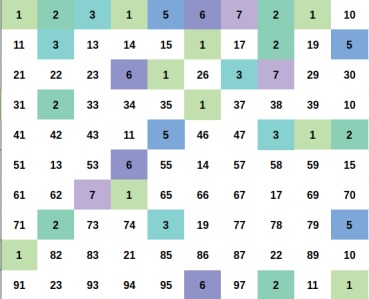
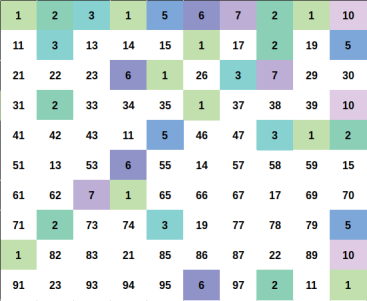
The statement:
Given three integers $$$n, k, p$$$, $$$(1 \leq k \leq n < p)$$$.
Count the number of array $$$a[]$$$ of size $$$k$$$ that satisfied
- $$$1 \leq a_1 < a_2 < \dots < a_k \leq n$$$
- $$$a_i \times a_j$$$ is perfect square $$$\forall 1 \leq i < j \leq k$$$
Since the number can be big, output it under modulo $$$p$$$.
For convenient, you can assume $$$p$$$ is a large constant prime $$$10^9 + 7$$$
Notice that in this blog, we will solve in $$$O(n)$$$ for general $$$k$$$ from the original task
For harder variants you can see in this blog [Variants] An interesting counting problem related to square product
Solution for k = 1
The answer just simply be $$$n$$$
Solution for k = 2
Problem
Given $$$n (1 \leq n \leq 10^6)$$$, count the number of pair $$$(a, b)$$$ that satisfied
- $$$1 \leq a < b \leq n$$$
- $$$a \times b$$$ is a perfect square.
Since the number can be big, output it under modulo $$$10^9 + 7$$$.
You can submit here: https://lqdoj.edu.vn/problem/aicprtsp2.
Examples
Algorithm
We need to count the number of pair $$$(a, b)$$$ that $$$1 \leq a < b \leq n$$$ and $$$a \times b$$$ is perfect square.
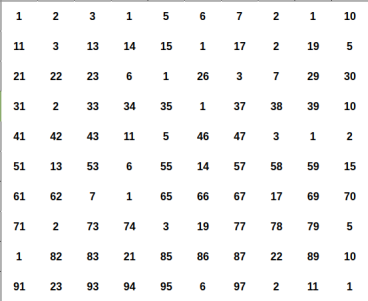
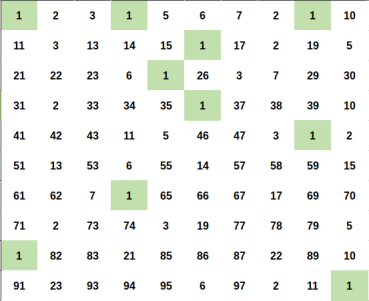
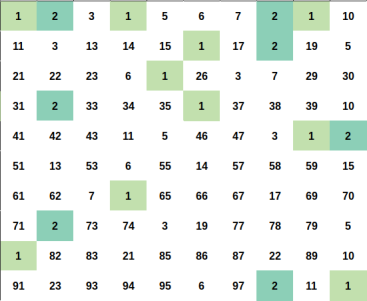
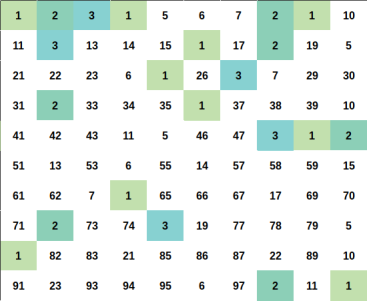
Every positive integer $$$x$$$ can be represent uniquely as $$$x = u \times p^2$$$ for some positive integer $$$u, p$$$ and $$$u$$$ as small as possible ($$$u$$$ is squarefree number).
Let represent $$$x = u \times p^2$$$ and $$$y = v \times q^2$$$ (still, minimum $$$u$$$, $$$v$$$ ofcourse).
We can easily proove that $$$x \times y$$$ is a perfect square if and if only $$$u = v$$$.
So for a fixed squarefree number $$$u$$$. You just need to count the number of ways to choose $$$p^2$$$.
The answer will be the sum of such ways for each fixed $$$u$$$.
Illustration
Implementation
Complexity
So about the complexity....
For the implementation using factorization, it is $$$O(n \log n)$$$.
For the 2 implementations below, the complexity is linear.
For the last implementation, the complexity is Linear
Solution for general k
Problem
Given $$$k, n (1 \leq k \leq n \leq 10^6)$$$, count the number of array $$$a[]$$$ of size $$$k$$$ that satisfied
- $$$1 \leq a_1 < a_2 < \dots < a_k \leq n$$$
- $$$a_i \times a_j$$$ is perfect square $$$\forall 1 \leq i < j \leq k$$$
Since the number can be big, output it under modulo $$$10^9 + 7$$$.
You can submit here: https://lqdoj.edu.vn/problem/aicprtspk.
For $$$k = 3$$$, you can subimit here: https://oj.vnoi.info/problem/dhbb2020_square.
Examples
Using the same logic above, we can easily solve the problem.
Now you face up with familliar binomial coefficient problem
This implementation here is using the assumption of $$$p$$$ prime and $$$p > max(n, k)$$$
You can still solve the problem for squarefree $$$p$$$ using lucas and CRT
Yet just let things simple as we only focus on the counting problem, we will assume $$$p$$$ is a large constant prime.
Extra Tasks
These are harder variants, and generalization from the original problem. You can see more detail here
A: Can we also use phi function or something similar to solve for $$$k = 2$$$ in $$$O(\sqrt{n})$$$ or faster ?
B: Can we also use phi function or something similar to solve for general $$$k$$$ in $$$O(\sqrt{n})$$$ or faster ?
C: Can we also solve the problem where there can be duplicate: $$$a_i \leq a_j\ (\forall\ i < j)$$$ and no longer $$$a_i < a_j (\forall\ i < j)$$$ ?
D: Can we solve the problem where there is no restriction between $$$k, n, p$$$ ?
E: Can we solve for negative integers, whereas $$$-n \leq a_1 < a_2 < \dots < a_k \leq n$$$ ?
F: Can we solve for a specific range, whereas $$$L \leq a_1 < a_2 < \dots < a_k \leq R$$$ ?
G: Can we solve for cube product $$$a_i \times a_j \times a_k$$$ effectively ?
H: Can we solve if it is given $$$n$$$ and queries for $$$k$$$ ?
I: Can we solve if it is given $$$k$$$ and queries for $$$n$$$ ?
J: Can we also solve the problem where there are no order: Just simply $$$1 \leq a_i \leq n$$$ ?
K: Can we also solve the problem where there are no order: Just simply $$$0 \leq a_i \leq n$$$ ?
M: Can we solve for $$$q$$$-product $$$a_{i_1} \times a_{i_2} \times \dots \times a_{i_q} = x^q$$$ (for given constant $$$q$$$) ?
N: Given $$$0 \leq \delta \leq n$$$, can we also solve the problem when $$$1 \leq a_1 \leq a_1 + \delta + \leq a_2 \leq a_2 + \delta \leq \dots \leq a_k \leq n$$$ ?
O: What if the condition is just two nearby elements and not all pairs. Or you can say $$$a_i \times a_{i+1} \forall 1 \leq i < n$$$ is a perfect square ?