466A - Cheap Travel
Solution of this problem is based on two claims:
— If m·a ≤ b then there is no point to buy a ride ticket.
— Sometimes it is better to buy summary more ride tickets for amount of rides than we need.
If we receive profits bying ride tickets then number of such ones will be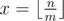 
. For the remain n - m·x rides we must choose the best variant: to buy separate ticket for each ride, or to buy ride ticket and use it not fully.
Complexity: O(1)
Solution: 7784793
466B - Wonder Room
Let’s assume that a ≤ b.
First of all, let’s consider the situation when we can already accommodate all the students. If 6·n ≤ a·b then answer is a·b a b.
Otherwise, we have to increase one of the walls(maybe, both). Let’s do it in the following way: iterate the size of the smallest wall newa (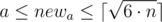
), after that we can calculate the size of another wall as 
.
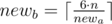For all this newa and newb if b ≤ newb we choose such a pair that has the smallest area of a room.
Obviously to undestrand, that there is no point to consider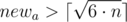 
because we can decrease it and receive room of smaller area when we know that 
.
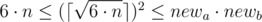Complexity: 
Solution: 7784788
466C - Number of Ways
First of all, notice that if sum of all elements is equal S then sum of each of three parts is equal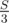 
.
Therefore, if S is not divided by 3 — then answer is 0.
Otherwise, let’s iterate the end of first part i (1 ≤ i ≤ n - 2) and if sum of 1..i elements is equal 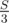then it means that we have to add to the answer the amount of such j (i + 1 < j) that the sum of elements from j-th to n-tn also equals .
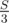Let’s create an array cnt[], where cnt[i] equals 1, if the sum of elements from i-th to n-th equals 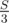and 0 — otherwise. Now, to calculate the answer we have to find the sum cnt[j] + cnt[j+1] + ... + cnt[n] faster then O(n). There are a lot of required ways to do this, but the easiest one is to create a new additional array sums[] where in j-th element will be cnt[j] + cnt[j+1] + ... + cnt[n]. It is easy to calculate in such way: sums[n] = cnt[n], sums[i] = sums[i+1] + cnt[i] (i < n).
Thus, we receive very simple solution: for each prefix of initial array 1..i with the sum that equals 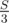we need to add to the answer sums[i+2].
Complexity: O(n)
Solution: 7784781
466D - Increase Sequence
Lets use dynamic programming to solve this problem. dp[i][opened] — the number of ways to cover prefix of array 1..i by segments and make it equal to h and remain after i-th element opened segments that are not closed.
Consider all possible variants opening/closing segments in each position:
- ] closing one segment
- [ opening one new segment
- [] adding one segment with length 1
- ][ closing one opened segment and opening a new one
- - do nothing
Lets understand how to build dynamic. It is obviously to understand that a[i] + opened can be equal h or h - 1. Otherwise, number of such ways equals 0.
Consider this two cases separately:
1) a[i] + opened = h
It means that number of opened segments after i-th as max as possible and we can’t open one more segment in this place. So there are two variants:
- [ Opening a new segment. If only opened > 0. dp[i][opened] += dp[i-1][opened + 1]
- - Do nothing. dp[i][opened] += dp[i-1][opened]
Other variants are impossible because of summary value of a[i] will be greater than h(when segment is finishing in current position — it increase value, but do not influence on opened, by the dynamic definition.
2) a[i] + opened + 1 = h
Here we consider ways where i-th element has been increased by opened + 1 segments, but after i-th remain only opened not closed segments. Therefore, there are next variants:
- ] — closing one of the opened segments(we can do it opened + 1 ways). dp[i][opened] += dp[i-1][opened + 1] * (opened + 1)
- [] — creating 1-length segment. dp[i][opened] += dp[i-1][opened]
- ][ — If only opened > 0. Amount of ways to choose segment which we will close equals opened. dp[i][opened] += dp[i-1][opened] * opened
Start values — dp[1][0] = (a[1] == h || a[1] + 1 == h?1:0); dp[1][1] = (a[1] + 1 == h?1:0)
Answer — dp[n][0].
Complexity: O(n)
Solution: 7784697
466E - Information Graph
Let’s introduce all structure of the company as a graph(if у is the head of х then we add edge y -> x). It is obviously to understand that after each operation our graph will be the set of trees. Actually, the third query — to check is our vertex belong to the subtree of the vertex which has received data package. Graph that we will receive after doing all operations we call final. Also, we will say that two vertexes belong to the same connectivity component if they belong to the same component in graph that we can have from final by changing directed edge to undirected.
Consider the following statement: vertex у is the parent of vertex х in current graph(after doing first i queries) if у and х belongs to the same conectitive component and in final graph у is the parent of х.
We will solve this problem offline. After each query of adding data package we will immediately answer all the questions about this package. Besides that, use disjoint set union to define is this vertex belong to the same component or not. To answer the question we need to check that y is the parent of x in final graph and that x and y is currently belong to the same connectivity component. Final graph we will build before doing this algorithm because we know all queries. Check that y is the parent of x in final tree we can simply in O(1) by arrays of entry-time and output-time which we can calculate use dfs(v —parent u <=> (in[v] ≤ in[u] and out[u] ≤ out[v]).
Complexity: O(n * u(n)), where u — inverse Ackerman function.
Solution: 7784662
