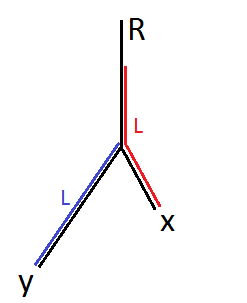
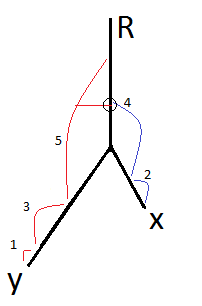
This is the first article I have written after a one-year pause. So let's just start...
Cutting to the chase
There are articles on LCA on many sites(Topcoder, Codeforces), Youtube videos, the Wiki is quite explicative. So why do I write this? The answer is actually simple. I have no friends.
On a more serious note, I think most LCA articles don't mention the off-line and no-query cases