Since I just achieved the rank of specialist in the first contest of 2024, I decided to make another AMA. Please use common sense before posting here.
→ Pay attention
Before contest
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
43:50:55
Register now »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
43:50:55
Register now »
*has extra registration
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Find user
→ Recent actions
Cyan is the color between blue and green. Its hex code is #00FFFF. Cyan is the complement of red, and it is the result when red is removed from white light.
Problem:
Let $$$n$$$ be a positive integer. A Japanese triangle consists of $$$1 + 2 + \dots + n$$$ circles arranged in an equilateral triangular shape such that for each $$$i = 1$$$, $$$2$$$, $$$\dots$$$, $$$n$$$, the $$$i^{th}$$$ row contains exactly $$$i$$$ circles, exactly one of which is coloured red. A ninja path in a Japanese triangle is a sequence of $$$n$$$ circles obtained by starting in the top row, then repeatedly going from a circle to one of the two circles immediately below it and finishing in the bottom row. Here is an example of a Japanese triangle with $$$n = 6$$$, along with a ninja path in that triangle containing two red circles.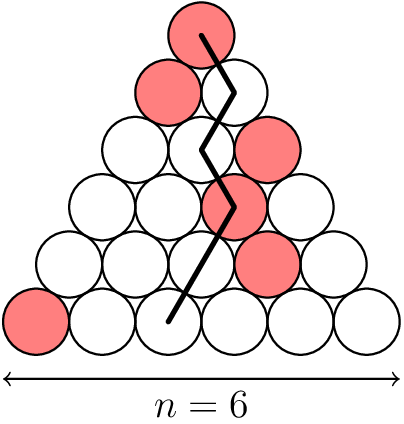 
Given a Japanese triangle, find the maximum number of red circles in a ninja path.
I found an algorithm using DP that can solve this problem in $$$O(n^2)$$$. Is there a more efficient solution?
Things I have heard of and know
- binary search
- coding
- addition and multiplication
- or, and, xor
- sorting
- fast io
- geometry (euclidean)
- geometry (complex numbers)
- angle chasing
- spiral similarity
- homography
- sharkydevil point
- pascal
- brianchon
- cayley-bacharach
- hyperbolas
- hall
- combinatorial nullstellenatz
- graph theory
- counting
- turan
- zsigmondy
- kobayashi
- factoring
- divisibility
- prime numbers
- quadratic reciprocity
- lifting the exponent
- Riemann zeta function
- analytic NT
- gaussian integers
- Fermat's Christmas Theorem
- cauchy
- jensen
- holder
- minkowski
- derivatives
- polynomials
- generating functions
If there are at least three things in this list you do not know, you are doing it wrong.
How do I make high quality problems?
In the recent div 3 and div 4 rounds, I keep getting hacked.
On my contests page, it shows that I solved 0 problems on the recent Division 3 round. However, my rank is still shown as 12 and my rating change is still +302. Is this a bug?
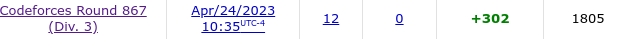
I solved 1799B Equalize by Divide using a constructive algorithm. I also noticed that there was a math tag on the problem. What's the math solution to this problem?
In this post, I want to go over each of my problems. I got this idea from antontrygubO_o and flamestorm.
| Number | Problem Statement | Source | Comments |
| 001 | In right triangle $$$ABC$$$, we have $$$\angle B=90^{\circ}$$$. If $$$AC=18$$$ and the length $$$x$$$ of the altitude from $$$B$$$ to $$$AC$$$ satisfies then the maximum possible value of the area of $ABC$ can be expressed in the form $$$\frac{a+b\sqrt c}d$$$ for integers $$$a$$$, $$$b$$$, $$$c$$$, and $$$d$$$, where $$$\gcd(a,b,d)=1$$$, $$$c$$$ is squarefree, and $$$d$$$ is positive. Compute $$$a+b+c+7d$$$. | CNCM PoTD 07/03/2021 | The answer is not $$$665$$$. |
| 002 | Let $$$n$$$ be a positive integer such that $$$n=a^{665}m$$$, where $$$a$$$ is as large as possible. Then, define $$$\psi(n)=\mu(m)$$$, where $$$\mu(n)=0$$$ if $$$p^2\mid n$$$ for some $$$p$$$, and $$$\mu(n)=(-1)^k$$$ if $$$n$$$ is squarefree and has $$$k$$$ prime factors. Find in terms of $n$. | CNCM PoTD 11/05/2021 | Classic summation swap with $$$665$$$. |
| 003 | Bob has infinitely many matches of equal length and wants to make as many equilateral triangles as possible. He uses one square yard of tape for each point two matches intersect. What is the smallest number of square inches of tape he needs to create at least seven equilateral triangles? | CNCM PoTD 11/14/2021 | Think outside the box and don't get trolled. |
| 004 | Let $$$ABC$$$ be a triangle such that $$$AB=7$$$, $$$BC=8$$$, and $$$CA=9$$$. There exists a unique point $$$X$$$ such that $$$XB=XC$$$ and $$$XA$$$ is tangent to the circumcircle of $$$ABC$$$. If $$$XA=\frac ab$$$, where $$$a$$$ and $$$b$$$ are coprime positive integers, find $$$a+b$$$. | OMMC 2022/11 | Nice length chasing problem with right triangles, but there are also a lot of bash solutions. |
| 005 | Alex writes down some distinct integers on a blackboard. For each pair of integers, he writes the positive difference of those on a piece of paper. Find the sum of all $$$n\leq2022$$$ such that it is possible for the numbers on the paper to contain all the positive integers between $$$1$$$ and $$$n$$$, inclusive exactly once. | OMMC Tiebreaker 2022/2 | Annoying grinding problem. |
| 006 | Compute the number of solutions in positive integers to the equation $$$ab+bc+ca=p^{2k}$$$ satisfying $$$a\leq b\leq c$$$ where $$$p$$$ is a prime and $$$k$$$ is a positive integer. | ELSMO Revenge 2022/1 | The solution may or may not exist. |
| 007 | Let $$$ABC$$$ be a triangle. Let $$$\omega_A$$$ be the ellipse with foci $$$B$$$ and $$$C$$$ passing through $$$A$$$, and define $$$\omega_B$$$ and $$$\omega_C$$$ similarly. Let $$$A_1$$$ and $$$A_2$$$ be the intersections of $$$\omega_B$$$ and $$$\omega_C$$$, and define $$$B_1$$$, $$$B_2$$$, $$$C_1$$$, and $$$C_2$$$ similarly. Show that $$$A_1A_2$$$, $$$B_1B_2$$$, and $$$C_1C_2$$$ are concurrent and find the point of concurrency. | OTIS Suggestion | Also Sharygin 2023/23 |
You can ask me anything on this blog.
Please do not troll.
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Nov/21/2024 21:44:06 (h1).
Desktop version, switch to mobile version.
Supported by
