Problem:
Let $$$n$$$ be a positive integer. A Japanese triangle consists of $$$1 + 2 + \dots + n$$$ circles arranged in an equilateral triangular shape such that for each $$$i = 1$$$, $$$2$$$, $$$\dots$$$, $$$n$$$, the $$$i^{th}$$$ row contains exactly $$$i$$$ circles, exactly one of which is coloured red. A ninja path in a Japanese triangle is a sequence of $$$n$$$ circles obtained by starting in the top row, then repeatedly going from a circle to one of the two circles immediately below it and finishing in the bottom row. Here is an example of a Japanese triangle with $$$n = 6$$$, along with a ninja path in that triangle containing two red circles. 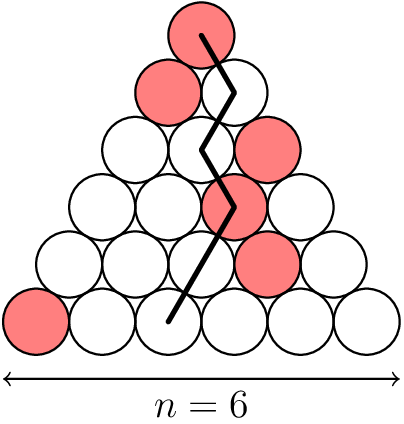
Given a Japanese triangle, find the maximum number of red circles in a ninja path.
I found an algorithm using DP that can solve this problem in $$$O(n^2)$$$. Is there a more efficient solution?










In the given example, Is the answer not 4 red circles.
Yes, the answer is 4. The diagram is only supposed to show what a ninja path is.
Define circle $$$(i, j)$$$ to be the circle at the $$$i$$$-th row from the top and the $$$j$$$-th from left of its row. Sort each red circle by $$$(i - j, j)$$$ and iterate it from smallest to largest. Define $$$dp_x$$$ to be the maximum number of red circle in the ninja path ending at some red circle which is the $$$x$$$-th from the left in its row. $$$dp_x$$$ = $$$max(dp_k) + 1$$$ where $$$1 \leq k \leq x$$$. We can speed this up using a segment tree in $$$O(n \log n)$$$.
I should really go sleep
Using Pólya urn model, one can find a probability distribution with which we have an equal probability of visiting each circle at each layer. We conclude, therefore, that the expected value of red circles is $$$1 + 1/2 + \dots + 1/n = O(\log n)$$$, so there always exists a ninja path with $$$O(\log n)$$$.
Actually, a sharper bound holds, $$$\lfloor \log_2 n \rfloor + 1$$$ (one can prove this via dyadic decomposition or its variations, so maybe there is another $$$O(n\log n)$$$ algorithm but which exploits this decomposition), which is reachable via the example of the following kind
Hi,
as you wrote
there always exists a ninja path with O(logn)How expected number of red balls assures the lenght of ninja path?
The expected value generally behaves like the average value. For the last one we have $$$\min A \leq avg A \leq \max A$$$, so if one has the average value $$$x$$$ then there exist both objects that contribute values $$$\geq avg A$$$ and objects that contribute $$$\leq avg A$$$. Of course, this works even if we work via asymptotic expressions rather than via their exact values. To get acquainted with this idea in further depth, I recommend reading about the probabilistic method.
Ok now my mind is a bit clearer. I think that if we index positions by both diagonals
and order things by first diagonal in increasing order, breaking ties by the second diagonal in increasing order, then this problem turns into longest non-decreasing subsequence, since from point (i, j) we can go to (i+1, j) or (i, j+1).
Hopefully I'm not brainfarting once again. Swistakk is right and I'm dumb. This is the simpler way to think about computing the answer from a configuration of balls though.
That Szekeres bound is wrong. You are fine with non-decreasing, but not that much with non-increasing
The optimal bound is $$$\lfloor \log_2 n \rfloor +1$$$ and the tight example was already shown above by miaowtin
The IMO problem asks to prove the optimal bound.
The proof of the bound is basically an observation on the DP rows (by how much their sum increases)
I've seen many solutions to this problem, but not this one? Could you elaborate?
The sum of values in a DP row will have to be at least (previous sum + maximum in previous row + 1). This can be shown by looking at the next row left and right of the maximum. The exact lower bound can be derived from this, and the example is tight.
I have no idea how you get this. I either don't understand what you mean or it's completely false. Imagine a dp row consisting of ten tens. In the row above you will not have values bigger than 11, so the sum will decrease. That's even more evident if you consider the top two rows (i.e. consisting of one and two balls). That's does not work out if you think of "diagonal rows" either
I think you don't understand. Here are a few DP rows from the optimal example:
Ah ok, you are thinking about dp from top to bottom, I was thinking about dp from bottom to top. All clear now, thanks :)