Hello Codeforces!
Lets discuss problems of the Poland contest. Any ideas on A? We came to the problem to count the number of minimal subsets with zero AND. How to count them?
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 168 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 159 |
| 5 | atcoder_official | 156 |
| 6 | djm03178 | 153 |
| 6 | adamant | 153 |
| 8 | luogu_official | 149 |
| 9 | awoo | 147 |
| 10 | TheScrasse | 146 |
Hello Codeforces!
Lets discuss problems of the Poland contest. Any ideas on A? We came to the problem to count the number of minimal subsets with zero AND. How to count them?
Легко видеть, что в задаче возможно всего три случая. Если король находится углу доски, то у него 3 возможных хода. Если он стоит на краю доски, то у него 5 возможных хода (если конечно он не в углу). Наконец, если король не стоит на краю доски, то у него всего 8 возожных хода.
char c, d;
bool read() {
return !!(cin >> c >> d);
}
void solve() {
int cnt = 0;
if (c == 'a' || c == 'h') cnt++;
if (d == '1' || d == '8') cnt++;
if (cnt == 0) puts("8");
else if (cnt == 1) puts("5");
else if (cnt == 2) puts("3");
else throw;
}
Сложность: O(1).
Легко видеть, что ответ всегд находится в одной из заданных точек (функция суммарного рассояния между парой заданных точек монотонна). Далее можно либо для каждой точки посчитать суммарное расстояние и выбрать оптимальную точку, либо заметить, что ответом является точка находящяяся посередине в отсортированном списке заданных точек (если точек чётное количетсво то слева посередине). Последний факт легко доказыватся, но можно это и не делать и сдать задачу первым способом.
const int N = 300300;
int n, a[N];
bool read() {
if (!(cin >> n)) return false;
forn(i, n) assert(scanf("%d", &a[i]) == 1);
return true;
}
void solve() {
sort(a, a + n);
li suml = 0, sumr = accumulate(a, a + n, 0ll);
li ansv = LLONG_MAX, ansp = LLONG_MIN;
forn(i, n) {
li curv = li(i) * a[i] - suml;
curv += sumr - li(n - i) * a[i];
if (ansv > curv) {
ansv = curv;
ansp = a[i];
}
suml += a[i];
sumr -= a[i];
}
assert(sumr == 0);
assert(ansv != LLONG_MAX);
cerr << "ansv: " << ansv << endl;
cout << ansp << endl;
}
Сложность: O(nlogn).
Задачу предложил Resul Hangeldiyev Resul.
Решение задачи легко получить из второго примера. Легко видеть, что если расставить все нечётные числа в виде ромба посередине квадрата, то мы получим магический квадрат.
int n;
bool read() {
return !!(cin >> n);
}
const int N = 101;
int a[N][N];
void solve() {
memset(a, 0, sizeof(a));
forn(i, n / 2) {
int len = n / 2 - i;
forn(j, len) {
int x1 = i, x2 = n - 1 - i;
int y1 = j, y2 = n - 1 - j;
a[x1][y1] = 1;
a[x1][y2] = 1;
a[x2][y1] = 1;
a[x2][y2] = 1;
}
}
int odd = 1, even = 2;
forn(i, n)
forn(j, n)
if (a[i][j]) a[i][j] = even, even += 2;
else a[i][j] = odd, odd += 2;
forn(i, n) {
forn(j, n) {
if (j) putchar(' ');
printf("%d", a[i][j]);
}
puts("");
}
}
Сложность: O(n2).
Эту задачу я уже давно хотел дать на раунд, она мне казалась очень стандартной, но я недооценил её сложность.
Запишем уравнение, которое описывает все решения задачи: a1k + b1 = a2l + b2 → a1k - a2l = b2 - b1. Имеем линейное диофантово уравнение с двумя неизвестными: Ax + By = C, A = a1, B = - a2, C = b2 - b1. Его решение имеет вид: 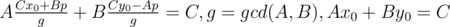 , где последнее уравнение решается с помощью расширенного алгоритма Евклида, а p произвольное целое число. Далее нам нужно удовлетворить двум условиям:
, где последнее уравнение решается с помощью расширенного алгоритма Евклида, а p произвольное целое число. Далее нам нужно удовлетворить двум условиям: 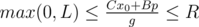 и
и 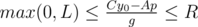 . Поскольку мы знаем знаки чисел A и B, последние уравнения задают отрезок возможных значений для переменной p, длина этого отрезка и является ответом на задачу.
. Поскольку мы знаем знаки чисел A и B, последние уравнения задают отрезок возможных значений для переменной p, длина этого отрезка и является ответом на задачу.
li a1, b1, a2, b2, l, r;
bool read() {
return !!(cin >> a1 >> b1 >> a2 >> b2 >> l >> r);
}
li _ceil(li, li);
li _floor(li a, li b) { return b < 0 ? _floor(-a, -b) : a < 0 ? -_ceil(-a, b) : a / b; }
li _ceil(li a, li b) { return b < 0 ? _ceil(-a, -b) : a < 0 ? -_floor(-a, b) : (a + b - 1) / b; }
li gcd(li a, li b, li& x, li& y) {
if (!a) {
x = 0, y = 1;
return b;
}
li xx, yy, g = gcd(b % a, a, xx, yy);
x = yy - b / a * xx;
y = xx;
return g;
}
void solve() {
l = max(0ll, _ceil(l - b1, a1));
r = _floor(r - b1, a1);
if (l > r) {
puts("0");
return;
}
li A = a1, B = -a2, C = b2 - b1;
li x0, y0;
li g = gcd(A, B, x0, y0);
if (C % g) {
puts("0");
return;
}
if (g < 0) {
g = -g;
x0 = -x0;
y0 = -y0;
}
li L = _ceil(r * g - x0 * C, B);
li R = _floor(l * g - x0 * C, B);
R = min(R, _floor(y0 * C, A));
li ans = max(0ll, R - L + 1);
cout << ans << endl;
}
Сложность: O(log(max(a1, a2))).
Задачу предложил Zi Song Yeoh zscoder.
У этой задачи есть простое решение, которое участники описали в комментариях. Моё решение несколько сложнее. Будем решать задачу с помощью динамического программирования. zn — наименьшее время, необходимое для получения n букв 'a'. Теперь рассмотрим переходы: переходы на дописывание одной буквы 'a' будем обрабатывать как обычно. Переходы на умножения на два и вычитание единицы будем обрабатыват одновременно: будем считать, что сразу после умножения числа i на двойку мы сразу сделаем i вычитаний и далее будем проталкивать от нашего числа вперёд такие обновления. Легко видеть, что такие обновления никогда не никогда не вкладываются, поэтому их можно хранить в очереди, дописывая очередное обновление в конец очереди, и, забирая лучшее обновление с начала очереди. Решение достаточно сложное на объяснение, но очень короткое, поэтому лучше посмотреть код :-)
int n;
li x, y;
bool read() {
return !!(cin >> n >> x >> y);
}
const int N = 20 * 1000 * 1000 + 13;
li z[N];
void solve() {
forn(i, N) z[i] = LLONG_MAX;
list<pair<li, int>> q;
z[0] = 0;
forn(i, n + 1) {
while (!q.empty() && q.front().y < i) q.pop_front();
if (!q.empty()) z[i] = min(z[i], q.front().x - i * x);
assert(z[i] != LLONG_MAX);
pair<li, int> cur(z[i] + y + 2 * i * x, 2 * i);
while (!q.empty() && q.back().x > cur.x) q.pop_back();
q.pb(cur);
z[i + 1] = min(z[i + 1], z[i] + x);
}
cout << z[n] << endl;
}
Сложность: O(n).
Задачу предложил Александр Кульков adamant.
Сначала научимся избавляться от запросов на удаление. В силу условия, что никакая строка не добавляется дважды (и, соответственно, не удаляется) нам достаточно посчитать ответ для всех добавленных строк (как будто они не удалялись) и вычесть из него ответ для уже удалённых. Таким образом, можно считать, что строки только добавляются.
Далее воспользуемся алгоритмом Ахо-Корасик. Единственная проблема, заключается в том, что алгоритм строит правильные суффиксные ссылки только после того как все строки добавлены. Чтобы решить эту проблему заметим, что ответ для набора строк равен ответу для некоторой части этого набора плюс ответ для оставшейся части. Далее воспользуемся стандартным приёмом превращения статической структуры данных (Ахо-Корасик в данном случае) в динамическую.
Пусть в данный момент в набор добавлено n строк, тогда мы будем хранить не более logn наборов строк размера разных степеней двойки. Добавим строку в набор размера нулевой степени двойки и далее перебрасывать наборы к большим степеням двойки, пока не получим инвариантный набор множеств.
Легко видеть, что каждая строка перебросится не более logm раз и на каждый запрос мы умеем отвечать за O(logm).
const int N = 4 * 300300, A = 26, LOGN = 20;
struct node {
char c;
int parent, link, output;
int next[A], automata[A];
int cnt;
node(char c = -1, int parent = -1, int link = -1, int output = -1, int cnt = -1):
c(c), parent(parent), link(link), output(output), cnt(cnt) {
memset(next, -1, sizeof(next));
memset(automata, -1, sizeof(automata));
}
};
node t[N];
vector<int> ids;
inline int get_idx() {
assert(!ids.empty());
int ans = ids.back();
ids.pop_back();
t[ans] = node();
return ans;
}
inline void return_idx(int idx) {
ids.pb(idx);
}
inline int add(const string& s, int root) {
int v = root;
forn(i, sz(s)) {
if (t[v].next[s[i] - 'a'] == -1) {
int idx = get_idx();
t[v].next[s[i] - 'a'] = idx;
t[idx] = node(s[i], v, -1, -1);
}
v = t[v].next[s[i] - 'a'];
}
t[v].output = v;
return v;
}
int link(int v, int root) {
int& ans = t[v].link;
if (ans != -1) return ans;
if (v == root || t[v].parent == root) return ans = root;
char c = t[v].c;
int vv = link(t[v].parent, root);
while (vv != root && t[vv].next[c - 'a'] == -1)
vv = link(vv, root);
return ans = (t[vv].next[c - 'a'] == -1? root: t[vv].next[c - 'a']);
}
int output(int v, int root) {
int& ans = t[v].output;
if (ans != -1) return ans;
return ans = (v == root? root: output(link(v, root), root));
}
int cnt(int v, int root) {
int& ans = t[v].cnt;
if (ans != -1) return ans;
v = output(v, root);
if (v == root) return ans = 0;
return ans = 1 + cnt(link(v, root), root);
}
int next(int v, char c, int root) {
int& ans = t[v].automata[c - 'a'];
if (ans != -1) return ans;
if (t[v].next[c - 'a'] != -1)
return ans = t[v].next[c - 'a'];
return ans = (v == root? root: next(link(v, root), c, root));
}
void dfs_clear(int v) {
forn(i, A) if (t[v].next[i] != -1) dfs_clear(t[v].next[i]);
return_idx(v);
}
string a[N];
int build(int root, const vector<int>& ids) {
dfs_clear(root);
root = get_idx();
forn(i, sz(ids)) add(a[ids[i]], root);
return root;
}
int calc(int root, int idx) {
int ans = 0;
const string& s = a[idx];
int v = root;
forn(i, sz(s)) {
v = next(v, s[i], root);
ans += cnt(v, root);
}
return ans;
}
int m;
bool read() {
return !!(cin >> m);
}
struct blocks {
int root[LOGN];
vector<int> block[LOGN];
void clear() {
forn(i, LOGN) {
block[i].clear();
root[i] = get_idx();
}
}
void insert(int i) {
vector<int> cur(1, i);
forn(i, LOGN)
if (sz(block[i]) == sz(cur)) {
cur.insert(cur.end(), all(block[i]));
block[i].clear();
root[i] = build(root[i], block[i]);
} else {
block[i] = cur;
root[i] = build(root[i], block[i]);
break;
}
}
li calc2(int idx) {
li ans = 0;
forn(i, LOGN) {
ans += calc(root[i], idx);
}
return ans;
}
};
char buf[N];
blocks z1, z2;
void solve() {
ids.clear();
nfor(i, N) ids.pb(i);
z1.clear();
z2.clear();
forn(i, m) {
int type;
assert(scanf("%d%s", &type, buf) == 2);
a[i] = buf;
if (type == 1) {
z1.insert(i);
} else if (type == 2) {
z2.insert(i);
} else if (type == 3) {
li ans = z1.calc2(i) - z2.calc2(i);
printf("%lld\n", ans);
fflush(stdout);
} else throw;
}
}
Сложность: O((slen + m)logm), где slen — суммарная длина всех строк во входном файле.
Привет, Codeforces!
22 августа 2016 года в 17:00 MSK состоится шестнадцатый учебный раунд Educational Codeforces Round 16 для участников из первого и второго дивизионов.
Это будет последний учебный раунд поготовленный мной. Как я уже ранее писал я начал работать в замечательной компании AIM Tech и теперь у меня стало заметно меньше времени на подготовку раундов. Не хочется из-за этого терять качество и интересность раундов, поэтому вскоре вы узнаете кто будет продолжать подготовку раундов.
Комплект задач был частично предложен участниками сообщества. Задачу C предложил Resul Hangeldiyev Resul. Задача E — это очередная задача предложенная Zi Song Yeoh zscoder. Задача F была предложена пользователем Александром Кульковым adamant. Оставшиеся задачи некоторое время крутились в моей голове и я наконец решил их дать на раунд (они являются достаточно стандартными, но важно уметь их хорошо решать).
Задачи для вас подготовил я (Эдвард Давтян). Спасибо Татьяне Семёновой Tatiana_S за проверку английских текстов условий. Большое спасибо Ивану Поповичу NVAL за вычитку и тестирование задач A-E и Александру Кулькову adamant за вычитку и тестирование задачи F.
На раунде вам по традиции будет предложено шесть задач. Надеюсь они вам понравятся! Думаю комплект задач получился чуть сложнее, чем обычно, но уверен это вас не остановит :-)
Good luck and have fun!

UPD 1: Завершено тестирование на взломах. Спасибо за участие!
UPD 2: Опубликован разбор задач.
Задачу предложил и подготовил Артур Яворски KingArthur.
В задаче нужно было просто сделать то, что написано в условии.
const int N = 1010;
int n, a[N];
bool read() {
if (!(cin >> n)) return false;
forn(i, n) assert(cin >> a[i]);
return true;
}
void solve() {
int cnt = accumulate(a, a + n, 0);
if (n == 1) puts(cnt == 1 ? "YES" : "NO");
else puts(cnt == n - 1 ? "YES" : "NO");
}
Сложность: O(n).
Задачу предложил Никита Мельников nickmeller.
В задаче нужно было аккуратно по картинке определить симметричные буквы, а также заметить, что пары букв (b, d) и (p, q) являются зеркальными отражениями.
string s;
bool read() {
return !!getline(cin, s);
}
string symmetric = "AHIMOoTUVvWwXxY";
map<char, char> opposite = {{'p', 'q'}, {'q', 'p'}, {'d', 'b'}, {'b', 'd'}};
void solve() {
forn(i, sz(s)) {
if (symmetric.find(s[i]) != string::npos) {
if (s[sz(s) - 1 - i] != s[i]) {
puts("NIE");
return;
}
} else if (opposite.count(s[i])) {
if ((sz(s) & 1) && i == (sz(s) >> 1)) {
puts("NIE");
return;
}
if (s[sz(s) - 1 - i] != opposite[s[i]]) {
puts("NIE");
return;
}
} else {
puts("NIE");
return;
}
}
puts("TAK");
}
Сложность: O(n).
Задачу предложил пользователь blowUpTheStonySilence.
Эта реализационная задача. Нужно было сделать ровно то, что написано в условии задачи. На мой взгляд, проще всего было найти позицию первой ненулевой цифры и позицию точки. Разность этих двух позиций равна числу b (если значение положительно нужно вычесть единичку).
string s;
bool read() {
return !!getline(cin, s);
}
void solve() {
int pos = int(find_if(all(s), [](char c) { return c != '0' && c != '.'; }) - s.begin());;
size_t dot_pos = s.find('.');
if (dot_pos == string::npos) {
dot_pos = s.size();
} else {
s.erase(dot_pos, 1);
}
int expv = (int) dot_pos - pos;
if (expv > 0) expv--;
forn(t, 2) {
while (s.back() == '0') s.pop_back();
reverse(all(s));
}
if (sz(s) > 1) s.insert(1, ".");
if (expv == 0) printf("%s\n", s.c_str());
else printf("%sE%d\n", s.c_str(), expv);
}
Сложность: O(n).
Задачу предложил Zi Song Yeoh zscoder.
Рассмотрим граф из n вершин, рёбрами которого являются заданные пары позиций. В каждой компоненте связности этого графа мы можем поменять значения в любых двух позициях. Соответственно мы можем все значения отсортировать в порядке убывания. Легко видеть, что полученная перестановка является лексикографически максимальной.
const int N = 1200300;
int n, m;
int p[N];
pti a[N];
bool read() {
if (!(cin >> n >> m)) return false;
forn(i, n) {
assert(scanf("%d", &p[i]) == 1);
p[i]--;
}
forn(i, m) {
assert(scanf("%d%d", &a[i].x, &a[i].y) == 2);
a[i].x--, a[i].y--;
}
return true;
}
bool used[N];
vector<int> g[N];
vector<int> perm, pos;
void dfs(int v) {
if (used[v]) return;
used[v] = true;
pos.pb(v);
perm.pb(p[v]);
for (auto to : g[v]) dfs(to);
}
int ans[N];
void solve() {
forn(i, n) {
g[i].clear();
used[i] = false;
}
forn(i, m) {
g[a[i].x].pb(a[i].y);
g[a[i].y].pb(a[i].x);
}
int cnt = 0;
forn(i, n)
if (!used[i]) {
cnt++;
pos.clear();
perm.clear();
dfs(i);
sort(all(pos));
sort(all(perm), greater<int>());
forn(j, sz(perm))
ans[pos[j]] = perm[j];
}
forn(i, n) {
if (i) putchar(' ');
printf("%d", ans[i] + 1);
}
puts("");
}
Сложность: O(n + m).
Задачу предложил Zi Song Yeoh zscoder.
Пусть zij — количество xor-последовательностей длины i с последним элементом aj. Пусть gij равно 1 если 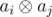 содержит количество единиц в бинарном представлении кратное трём, и равно 0 в противном случае. Расмотрим векторы чисел zi = {zij}, zi - 1 = {zi - 1, j} и матрицу G = {gij}. Легко видеть, что zi = G × zi - 1. Соответственно, zn = Gn × z0. В силу ассоциативности операции матричного умножения можно сначала вычислать Gn бинарным возведением в степень матрицы и затем умножить полученную матрицу на z0.
содержит количество единиц в бинарном представлении кратное трём, и равно 0 в противном случае. Расмотрим векторы чисел zi = {zij}, zi - 1 = {zi - 1, j} и матрицу G = {gij}. Легко видеть, что zi = G × zi - 1. Соответственно, zn = Gn × z0. В силу ассоциативности операции матричного умножения можно сначала вычислать Gn бинарным возведением в степень матрицы и затем умножить полученную матрицу на z0.
const int N = 101;
int n;
li k;
li a[N];
bool read() {
if (!(cin >> n >> k)) return false;
forn(i, n) assert(cin >> a[i]);
return true;
}
const int mod = 1000 * 1000 * 1000 + 7;
inline int add(int a, int b) { return a + b >= mod ? a + b - mod : a + b; }
inline void inc(int& a, int b) { a = add(a, b); }
inline int mul(int a, int b) { return int(a * 1ll * b % mod); }
int count(li x) {
int ans = 0;
while (x) {
ans++;
x &= x - 1;
}
return ans;
}
void mul(int a[N][N], int b[N][N], int n) {
static int c[N][N];
forn(i, n)
forn(j, n) {
c[i][j] = 0;
forn(k, n) inc(c[i][j], mul(a[i][k], b[k][j]));
}
forn(i, n) forn(j, n) a[i][j] = c[i][j];
}
void bin_pow(int a[N][N], li b, int n) {
static int ans[N][N];
forn(i, n) forn(j, n) ans[i][j] = i == j;
while (b) {
if (b & 1) mul(ans, a, n);
mul(a, a, n);
b >>= 1;
}
forn(i, n) forn(j, n) a[i][j] = ans[i][j];
}
void solve() {
static int a[N][N];
memset(a, 0, sizeof(a));
forn(i, n) {
forn(j, n)
a[i][j] = count(::a[i] ^ ::a[j]) % 3 == 0;
a[i][n] = 1;
}
//forn(i, n + 1) clog << mp(a[i], n + 1) << endl;
bin_pow(a, k, n + 1);
int ans = 0;
forn(i, n + 1) inc(ans, a[i][n]);
cout << ans << endl;
}
Сложность: O(n3logk).
Задачу предложил Michael Kirsche mkirsche.
Будем считать количество пар с произведением меньшим p. Получить количество не меньших, можно вычитая из общего количества пар n·(n - 1) количество меньших. Пусть cnti количество чисел в a раных i, а zj — количество пар из a с произведением равным j. Для подсчета массива z можно воспользоваться по сути решетом Эратосфена: переберём первое число a, а также кратное ему b = ka и увеличим zb на величину cnta·cntk. После предподсчёта массива z достаточно предподсчитать массив его частичных сумм, чтобы отвечать на запросы о количество пар меньших p.
const int N = 3100300;
int n, m;
int a[N], p[N];
bool read() {
if (!(cin >> n)) return false;
forn(i, n) assert(scanf("%d", &a[i]) == 1);
assert(cin >> m);
forn(i, m) assert(scanf("%d", &p[i]) == 1);
return true;
}
int cnt[N];
li z[N];
void solve() {
memset(cnt, 0, sizeof(cnt));
forn(i, n) cnt[a[i]]++;
fore(a, 1, N) {
if (!cnt[a]) continue;
for (int b = a; b < N; b += a) {
if (b / a != a) z[b] += li(cnt[a]) * cnt[b / a];
else z[b] += li(cnt[a]) * (cnt[a] - 1);
}
}
fore(i, 1, N) z[i] += z[i - 1];
forn(i, m) {
li ans = li(n) * (n - 1) - z[p[i] - 1];
printf("%lld\n", ans);
}
}
Сложность: O(n + XlogX), где X — наибольшее значение в массиве p.
Привет, Codeforces!
13 июля 2016 года в 19:00 MSK состоится четырнадцатый учебный раунд Educational Codeforces Round 14 для участников из первого и второго дивизионов.
<У меня уже накопился большой список задач, пожалуйста не расстраивайтесь, если ваша задача долго не попадает в раунд>
О формате и деталях проведения учебных раундов я писал уже ранее. Также об учебных раундах вы можете прочитать здесь.
Раунд будет нерейтинговым. Соревнование будет проводиться по немного расширенным правилам ACM ICPC. На решение задач у вас будет два часа. После окончания раунда будет период времени длительностью в один день, в течение которых вы можете попробовать взломать абсолютно любое решение (в том числе свое). Причем исходный код будет предоставлен не только для чтения, но и для копирования. Таким образом вы можете локально тестировать решение, которое хотите взломать, или, например, запустить стресс-тест.
Если у вас есть идеи каких-то задач, которые вам кажутся интересными, или может есть уже что-то почти готовое, что вы по каким-то причинам не можете дать на раунд (злой координатор сказал, что задача БАЯН), официальное соревнование (жюри не хочет переграбливать соревнование), можете писать мне.
Не стесняйтесь присылать как простые (и даже очень простые), так и сложные задачи (но обязательно интересные). Просьба присылать задачи к которым вы знаете решение, с понятным условием (наличие легенды исключительно по вашему желанию), а также сопровождать условия одним-двумя примерами, чтобы можно было быстро убедиться в правильности понимания условия.
Благодарю их и всех кто присылает задачи! Количество, присланных, но ещё не использованных задач постепенно растёт. Если я нигде ничего не потерял, то я уже ответил всем кто прислал мне задачи более 5-6 дней назад. Прошу с пониманием отнестись в случае, если ваша задача долго не появляется.
</У меня уже накопился большой список задач, пожалуйста не расстраивайтесь, если ваша задача долго не попадает в раунд>
Комплект задач был предложен участниками сообщества. Задачу А предложил и подготовил Артур Яворски KingArthur. Задачу B прислал Никита Мельников nickmeller. Задачу C предложил пользователь blowUpTheStonySilence. Задачи D и E из большого комплекта задач присланных Zi Song Yeoh zscoder (он, кстати, сейчас участвует в IMO, пожелаем ему удачи). Задача F была предложена пользователем Michael Kirsche mkirsche.
Как я уже говорил задачу A подготовил Артур Яворски KingArthur, остальные задачи для вас подготовил я (Эдвард Давтян). Спасибо Татьяне Семёновой Tatiana_S за проверку английских текстов условий. Задачи вычитывали и тестировали пользователи, предложившие их, соответственно Артур Яворски KingArthur, Никита Мельников nickmeller, пользователь blowUpTheStonySilence и Michael Kirsche mkirsche. Большое им за это спасибо!
На раунде вам по традиции будет предложено шесть задач. Надеюсь они вам понравятся! Комплект задач должен получиться сбалансированным и, на мой взгляд, не сложным.
Good luck and have fun!
UPD 1: Все взломы по задаче D будут перетестированы.
UPD 2: Фаза открытых взломов будет продлена до завтра.
UPD 3: Прошу прощения за проблемы в задаче D. Решения получающие WA3 были перетестированы. Теперь все в порядке.
UPD 4: Соревнование завершено. Все решения протестированы на полном наборе тестов. Вскоре появится разбор задач.
UPD 5: Разбор задач опубликован.

Задачу предложил Әбдірахман Исмаил bash.
Нам нужно найти минимальное x, что x * k > n. Легко видеть, что 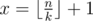 . Для подробного знакомства с математическими функциями пола и потолка я рекомендую книгу авторов Грэхем, Кнут, Паташник "Конкретная математика". В этой книге есть отдельная глава, посвящённая этим функциям и их свойствам.
. Для подробного знакомства с математическими функциями пола и потолка я рекомендую книгу авторов Грэхем, Кнут, Паташник "Конкретная математика". В этой книге есть отдельная глава, посвящённая этим функциям и их свойствам.
li n, k;
bool read() {
return !!(cin >> n >> k);
}
void solve() {
cout << (n / k + 1) * k << endl;
}
Сложность: O(1).
Задачу предложил Артур Яворски KingArthur.
Два календаря совпадают если и только, если в них одинаковое количество дней и они начинаются с одного дня недели. Таким образом, достаточно было просто перебрать следующий год, поддерживая первый день недели в году. На самом деле день недели каждый год увеличивается на единицу. Исключением являются високосные годы, когда день недели увеличивается на два.
int y;
bool read() {
return !!(cin >> y);
}
bool leap(int y) {
return y % 400 == 0 || (y % 4 == 0 && y % 100 != 0);
}
void solve() {
bool is_leap = leap(y);
int d = 0;
do {
d++;
if (leap(y)) d++;
y++;
d %= 7;
} while (d || leap(y) != is_leap);
cout << y << endl;
}
Сложность: O(1) — легко видеть, что количество итерация не превосходит небольшой константы.
Задачу предложил Sheikh Monir skmonir.
Легко видеть, что в оба цвета мы можем покрасить доски с номерами кратными lcm(a, b) — НОК чисел a и b. Очевидно, что эти доски выгоднее красить в более дорогой цвет. Таким образом, ответ равен: 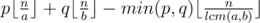 .
.
li n, a, b, p, q;
bool read() {
return !!(cin >> n >> a >> b >> p >> q);
}
li gcd(li a, li b) { return !a ? b : gcd(b % a, a); }
li lcm(li a, li b) { return a / gcd(a, b) * b; }
void solve() {
li ans = 0;
ans += (n / a) * p;
ans += (n / b) * q;
ans -= (n / lcm(a, b)) * min(p, q);
cout << ans << endl;
}
Сложность: O(log(max(a, b))).
Задачу предложил Zi Song Yeoh zscoder.
В этой задаче можно было вывести формулу в качестве ответа: для этого нужно было посчитать сумму геометрической прогрессии. Далее формулу было легко посчитать с помощью бинарного возведения в степень.
Я опишу более сложное, но более общее решение. Если у нас есть некоторый набор переменных, который пошагово пересчитывается друг через друга с помощью линейной функции, то можно применить бинарное возведение в степень матрицы. Итак, в нашей задаче переменная была одна x. Новая переменная x' получалась по формуле A·x + B. Рассмотрим матрицу z = [[A, B], [0, 1]] и вектор v = [x, 1]. Умножим z на v слева. Легко видеть, что получится вектор v' = [x', 1]. Таким образом, чтобы сделать n итераций, мы просто должны n раз умножить слева матрицу z на вектор v. В силу свойства ассоциативности операции умножения матриц перемножение мы можем сделать бинарно.
В качестве упражнения можете попробовать выписать самостоятельно матрицу для чисел Фиббоначи и научиться их быстро считать. Под спойлером матрица и вектор.
z=[[0, 1], [1, 1]], v=[0, 1].
int A, B, x;
li n;
bool read() {
return !!(cin >> A >> B >> n >> x);
}
const int mod = 1000 * 1000 * 1000 + 7;
inline int add(int a, int b) { return a + b >= mod ? a + b - mod : a + b; }
inline int mul(int a, int b) { return int(a * 1ll * b % mod); }
inline void inc(int& a, int b) { a = add(a, b); }
void mul(int a[2][2], int b[2][2]) {
static int res[2][2];
forn(i, 2)
forn(j, 2) {
res[i][j] = 0;
forn(k, 2) inc(res[i][j], mul(a[i][k], b[k][j]));
}
forn(i, 2) forn(j, 2) a[i][j] = res[i][j];
}
void bin_pow(int a[2][2], li b) {
static int res[2][2];
forn(i, 2) forn(j, 2) res[i][j] = i == j;
while (b) {
if (b & 1) mul(res, a);
mul(a, a);
b >>= 1;
}
forn(i, 2) forn(j, 2) a[i][j] = res[i][j];
}
void solve() {
int z[2][2] = {
{ A, B },
{ 0, 1 }
};
bin_pow(z, n);
int result = add(mul(z[0][0], x), z[0][1]);
cout << result << endl;
}
Сложность: O(logn).
Задачу предложил и подготовил Алексей Дергунов dalex.
Давайте решать задачу динамикой. zmask, i — наибольшая вероятность выиграть Ивану, если джедаи из маски mask уже хоть раз сражались, а в живых остался только i-й джедай. Для подсчёта динамики переберём следующего джедая (ему придётся сражаться против i-го джедая): 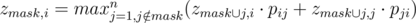 .
.
const int N = 20, EXPN = (1 << 18) + 3;
int n;
ld p[N][N];
bool read() {
if (!(cin >> n)) return false;
forn(i, n) forn(j, n) assert(cin >> p[i][j]);
return true;
}
ld z[EXPN][N];
ld solve(int mask, int i) {
ld& ans = z[mask][i];
if (ans > -0.5) return ans;
if (mask == (1 << n) - 1) return ans = !i;
ans = 0;
forn(j, n)
if (!(mask & (1 << j))) {
ld cur = 0;
cur += solve(mask | (1 << j), i) * p[i][j];
cur += solve(mask | (1 << j), j) * p[j][i];
ans = max(ans, cur);
}
return ans;
}
void solve() {
if (n == 1) {
puts("1");
return;
}
forn(i, 1 << n) forn(j, n) z[i][j] = -1;
ld ans = 0;
forn(i, n)
forn(j, i) {
int mask = (1 << i) | (1 << j);
ld cur = 0;
cur += solve(mask, i) * p[i][j];
cur += solve(mask, j) * p[j][i];
ans = max(ans, cur);
}
cout << ans << endl;
}
Сложность по времени: O(2nn2).
Сложность по памяти: O(2nn).
Задачу предложил AmirMohammad Dehghan PrinceOfPersia.
Посмотрим на задачу геометрически: пары чисел в множестве это просто прямые, задача по вертикальной прямой найти самое верхнее её пересечение с какой-либо прямой.
Разобьём все запросы на  блоков. Рассмотрим те прямые, которые были добавлены до начала блока и не будут удалены в нём. Построим по этому множеству нижнее огибающее множество. Теперь, чтобы ответить на один запрос третьего типа нужно взять максимум по прямым нижнего огибающего множества и по запросам в блоке до текущего запроса. Последних не более
блоков. Рассмотрим те прямые, которые были добавлены до начала блока и не будут удалены в нём. Построим по этому множеству нижнее огибающее множество. Теперь, чтобы ответить на один запрос третьего типа нужно взять максимум по прямым нижнего огибающего множества и по запросам в блоке до текущего запроса. Последних не более  , поэтому по ним мы можем пройти в лоб и обновить ответ. Теперь посмотрим на все запросы в блоке третьего типа, отсортируем их слева направо и будет искать оптимальную прямую в огибающем множестве с помощью двух указателей.
, поэтому по ним мы можем пройти в лоб и обновить ответ. Теперь посмотрим на все запросы в блоке третьего типа, отсортируем их слева направо и будет искать оптимальную прямую в огибающем множестве с помощью двух указателей.
const int N = 300300;
int n;
int t[N], a[N], b[N], id[N], q[N];
bool read() {
if (!(cin >> n)) return false;
forn(i, n) {
assert(scanf("%d", &t[i]) == 1);
if (t[i] == 1) {
assert(scanf("%d%d", &a[i], &b[i]) == 2);
} else if (t[i] == 2) {
assert(scanf("%d", &id[i]) == 1);
id[i]--;
} else if (t[i] == 3) {
assert(scanf("%d", &q[i]) == 1);
} else throw;
}
return true;
}
bool in_set[N], deleted[N];
vector<pair<pti, int>> lines;
vector<pti> envelope;
void build_envelope() {
envelope.clear();
envelope.reserve(n);
forn(ii, sz(lines)) {
int i = lines[ii].y;
if (in_set[i] && !deleted[i]) {
assert(t[i] == 1);
pti c(a[i], b[i]);
while (!envelope.empty()) {
pti b = envelope.back();
if (b.x == c.x) {
envelope.pop_back();
continue;
} else if (sz(envelope) > 1) {
pti a = envelope[sz(envelope) - 2];
ld xc = ld(c.y - a.y) / (a.x - c.x);
ld xb = ld(b.y - a.y) / (a.x - b.x);
if (xc < xb) {
envelope.pop_back();
continue;
}
}
break;
}
envelope.pb(c);
}
}
}
li ans[N];
vector<pti> qs;
void process_qs() {
sort(all(qs));
int p = 0;
forn(i, sz(qs)) {
li q = qs[i].x;
int id = qs[i].y;
while (p + 1 < sz(envelope)) {
li cval = envelope[p].x * q + envelope[p].y;
li nval = envelope[p + 1].x * q + envelope[p + 1].y;
if (cval > nval) break;
p++;
}
if (p < sz(envelope)) {
ans[id] = envelope[p].x * q + envelope[p].y;
}
}
}
void solve() {
lines.clear();
lines.reserve(n);
forn(i, n) if (t[i] == 1) lines.pb(mp(mp(a[i], b[i]), i));
sort(all(lines));
memset(in_set, false, sizeof(in_set));
memset(deleted, false, sizeof(deleted));
forn(i, n) ans[i] = LLONG_MIN;
int blen = int(sqrtl(n));
blen = 2500;
for (int l = 0; l < n; l += blen) {
int r = min(n, l + blen);
memset(deleted, false, sizeof(deleted));
fore(i, l, r) if (t[i] == 2) deleted[id[i]] = true;
build_envelope();
qs.clear();
qs.reserve(r - l);
fore(i, l, r) if (t[i] == 3) qs.pb(mp(q[i], i));
process_qs();
fore(i, l, r) {
if (t[i] == 1) in_set[i] = true;
else if (t[i] == 2) in_set[id[i]] = false;
else {
fore(j, l, r) {
if (t[j] == 1 && in_set[j])
ans[i] = max(ans[i], li(a[j]) * q[i] + b[j]);
else if (t[j] == 2 && in_set[id[j]])
ans[i] = max(ans[i], li(a[id[j]]) * q[i] + b[id[j]]);
}
if (ans[i] != LLONG_MIN) printf("%lldn", ans[i]);
else puts("EMPTY SET");
}
}
}
}
Сложность: 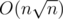 .
.
Привет, Codeforces!
13 июня 2016 года в 19:00 MSK состоится очередной тринадцатый учебный раунд Educational Codeforces Round 13 для участников из первого и второго дивизионов. С прошлого раунда прошло почти два месяца. Столь долгий перерыв связан с несколькими обстоятельствами: 1) в конце апреля я координировал обычный CF-раунд; 2) после этого был месяц, когда большая часть сообщества СП (включая меня) была занята подготовкой и участием в ACM ICPC WF; 3) наконец, в начале этого месяца я начал работать в компании AimTech (надеюсь у меня по прежнему будет достаточно времени, чтобы готовить учебные раунды).
<Стоит хоть раз почитать то, что здесь находится, вдруг есть что-то интересное или ошибки может>
О формате и деталях проведения учебных раундов я писал уже ранее. Также об учебных раундах вы можете прочитать здесь.
Раунд будет нерейтинговым. Соревнование будет проводиться по немного расширенным правилам ACM ICPC. На решение задач у вас будет два часа. После окончания раунда будет период времени длительностью в один день, в течение которых вы можете попробовать взломать абсолютно любое решение (в том числе свое). Причем исходный код будет предоставлен не только для чтения, но и для копирования. Таким образом вы можете локально тестировать решение, которое хотите взломать, или, например, запустить стресс-тест.
Если у вас есть идеи каких-то задач, которые вам кажутся интересными, или может есть уже что-то почти готовое, что вы по каким-то причинам не можете дать на раунд (злой координатор сказал, что задача БАЯН), официальное соревнование (жюри не хочет переграбливать соревнование), можете писать мне.
Не стесняйтесь присылать как простые (и даже очень простые), так и сложные задачи (но обязательно интересные). Просьба присылать задачи к которым вы знаете решение, с понятным условием (наличие легенды исключительно по вашему желанию), а также сопровождать условия одним-двумя примерами, чтобы можно было быстро убедиться в правильности понимания условия.
</Стоит хоть раз почитать то, что здесь находится, вдруг есть что-то интересное или ошибки может>
Комплект задач был предложен участниками сообщества. Задачу А предложил Әбдірахман Исмаил bash. Задачу B прислал Артур Яворски KingArthur. Задачу C предложил Sheikh Monir skmonir. Задача D одна из большого количества задач присланных Zi Song Yeoh zscoder (и их ещё много осталось). Задача E была предложена и полностью подготовлена Алексеем Дергуновым dalex: её я хотел взять ещё в прошлый раунд, но она оказалась сложноватой для задачи D. Наконец, упрощённую версию задачи F предложил AmirMohammad Dehghan PrinceOfPersia (я её несколько усложнил).
Благодарю их и всех кто присылает задачи! Количество, присланных, но ещё не использованных задач постепенно растёт. Если я нигде ничего не потерял, то я уже ответил всем кто прислал мне задачи более 5-6 дней назад. Прошу с пониманием отнестись в случае, если ваша задача долго не появляется.
Как я уже говорил задачу E подготовил Алексей Дергунов, остальные задачи для вас подготовил я (Эдвард Давтян). Спасибо Татьяне Семёновой Tatiana_S за проверку английских текстов условий. Задачи вычитывали и тестировали пользователи, предложившие их, соответственно Әбдірахман Исмаил bash, Артур Яворски KingArthur, Sheikh Monir skmonir, Zi Song Yeoh zscoder, Алексей Дергунов dalex и AmirMohammad Dehghan PrinceOfPersia. Большое им за это спасибо!
На раунде вам по традиции будет предложено шесть задач. Надеюсь они вам понравятся! В прошлый раз я немного неудачно подобрал комплект и он оказался чересчур сложным. В этот раз я решил исправить это. Задачи будут проще обычного.
Good luck and have fun!
Это, кстати первый летний раунд :-)
UPD: Раунд закончен. Разбор задач опубликован.

Hey, Codeforces!
I've just submitted a solution for a SPOJ problem and get strange verdict. I'm using SPOJ for the first time and can't find any FAQ section there. What does it mean? And why my submission is black?

Задачу предложил Сергей Эрлих unprost.
Рассмотрим интервал времени, когда Симион будет находиться на трассе строго между городами (x1, y1), (x1 = 60h + m, y1 = x1 + ta). Переберём встречный автобус. Пусть (x2, y2) — это интервал времени, когда встречный автобус будет находиться строго между городами. Если пересечение этих интервалов (x = max(x1, x2), y = min(y1, y2)) не пусто, то Симион посчитает этот автобус.
int a, ta;
int b, tb;
int h, m;
bool read() {
if (!(cin >> a >> ta)) return false;
assert(cin >> b >> tb);
assert(scanf("%d:%d", &h, &m) == 2);
return true;
}
void solve() {
int x1 = h * 60 + m;
int y1 = x1 + ta;
int ans = 0;
for (int x2 = 5 * 60 + 0; x2 < 24 * 60; x2 += b) {
int y2 = x2 + tb;
int x = max(x1, x2), y = min(y1, y2);
if (x < y)
ans++;
}
cout << ans << endl;
}
Сложность: O(1).
Задачу предложил Ayush Anand JeanValjean01.
В этой задаче нужно было сделать ровно то, что написано в условии. Никаких хитростей и подвохов.
const int N = 111;
int n, m, k;
int p[N];
int a[N][N];
bool read() {
if (!(cin >> n >> m >> k)) return false;
forn(i, k) {
assert(scanf("%d", &p[i]) == 1);
p[i]--;
}
forn(i, n)
forn(j, m) {
assert(scanf("%d", &a[i][j]) == 1);
a[i][j]--;
}
return true;
}
void solve() {
int ans = 0;
forn(i, n)
forn(j, m) {
int pos = int(find(p, p + k, a[i][j]) - p);
ans += pos + 1;
nfor(l, pos) p[l + 1] = p[l];
p[0] = a[i][j];
}
cout << ans << endl;
}
Сложность: O(nmk).
Задачу предложил Zi Song Yeoh zscoder.
Для решения этой задачи есть два подхода: жадность и динамическое программирование.
Первый подход: Рассмотрим некоторый отрезок из подряд идущих одинаковых букв. Пусть длина отрезка k. Очевидно мы должны изменить хотя бы 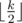 букв в ней, чтобы не было одинаковых букв подряд. С другой стороны мы можем изменить второй, четвёртый и т.д. символы на букву, которая не равна букве слева и справа от нашего отрезка.
букв в ней, чтобы не было одинаковых букв подряд. С другой стороны мы можем изменить второй, четвёртый и т.д. символы на букву, которая не равна букве слева и справа от нашего отрезка.
const int N = 200200;
int n;
char s[N];
bool read() {
if (!gets(s)) return false;
n = int(strlen(s));
return true;
}
void solve() {
for (int i = 0, j = 0; i < n; i = j) {
while (j < n && s[j] == s[i]) j++;
char c = 'a';
while (c == s[i] || (i > 0 && c == s[i - 1]) || (j < n && c == s[j]))
c++;
fore(k, i, j)
if ((i + k) & 1)
s[k] = c;
}
puts(s);
}
Второй подход: Пусть zka — наименьшее количество изменений, чтобы на префиксе длины k не было двух подряд идущих одинаковых букв и при этом символ s'k был равен букве a. Переберём букву, которую поставим на k + 1-й позиции и если она не равна a сделаем переход. Цена перехода равна 0, если мы поставили ту же букву, что стояла в исходной строке s на k + 1-й позиции. В противном случае цена равна 1.
const int N = 1200300, A = 27;
int n;
char s[N];
bool read() {
if (!gets(s)) return false;
n = int(strlen(s));
return true;
}
int z[N][A];
int p[N][A];
char ans[N];
void solve() {
memset(z, 63, sizeof(z));
z[0][A - 1] = 0;
forn(i, n) {
int c = int(s[i] - 'a');
forn(j, A) {
int dv = z[i][j];
if (dv > INF / 2) continue;
forn(nj, A - 1) {
if (nj == j) continue;
int ct = nj != c;
if (z[i + 1][nj] > dv + ct) {
z[i + 1][nj] = dv + ct;
p[i + 1][nj] = j;
}
}
}
}
int idx = int(min_element(z[n], z[n] + A) - z[n]);
for (int i = n, j = idx; i > 0; j = p[i][j], i--)
ans[i - 1] = char('a' + j);
ans[n] = 0;
cerr << z[n][idx] << endl;
puts(ans);
}
Сложность: O(n).
Задачу предложил Zi Song Yeoh zscoder.
Рассмотрим подмножество A, являющееся ответом на задачу. Пусть a, b, c — три произвольных элемента из A и пусть не более чем один из них равен 1. По принципу Дирихле среди этих трёх чисел обязательно найдется пара чисел с одинаковой чётностью. Поскольку в этой паре только одно может быть равно 1, то их сумма чётна и больше 2. Значит подмножество A не является простым. Таким образом, A состоит либо из двух чисел больших единицы (с простой суммой), либо из некоторого количества единиц и возможно одной не единицы (если она равна простому минус один). Первый случай легко обработать за O(n2). Второй случай легко обрабатывается за линейное время. Среди двух ответов, конечно, нужно просто выбрать лучший.
Проверять на простоту числа порядка 2·106 за O(1) можно с помощью обычного или линейного решета Эратосфена.
const int N = 1010, X = 2100300;
int n, a[N];
bool read() {
if (!(cin >> n)) return false;
forn(i, n) assert(scanf("%d", &a[i]) == 1);
return true;
}
int szp, p[X];
int mind[X];
void prepare() {
fore(i, 2, X) {
if (!mind[i]) {
p[szp++] = i;
mind[i] = i;
}
for (int j = 0; j < szp && p[j] <= mind[i] && i * p[j] < X; j++)
mind[i * p[j]] = p[j];
}
}
void printAns(int cnt1, int a = -1, int b = -1) {
vector<int> ans;
forn(i, cnt1) ans.pb(1);
if (a != -1) ans.pb(a);
if (b != -1) ans.pb(b);
assert(!ans.empty());
random_shuffle(all(ans));
cout << sz(ans) << endl;
forn(i, sz(ans)) {
if (i) putchar(' ');
printf("%d", ans[i]);
}
puts("");
}
void solve() {
int cnt1 = (int) count(a, a + n, 1);
function<bool(int)> isPrime = [](int p) { return mind[p] == p; };
if (cnt1 > 0)
forn(i, n)
if (a[i] != 1 && isPrime(a[i] + 1)) {
printAns(cnt1, a[i]);
return;
}
if (cnt1 > 1) {
printAns(cnt1);
return;
}
forn(i, n)
forn(j, i)
if (isPrime(a[i] + a[j])) {
printAns(0, a[i], a[j]);
return;
}
printAns(0, a[0]);
}
Сложность: O(n2 + X), где X — максимальное среди заданных чисел.
Задачу предложил Zi Song Yeoh zscoder.
Знак  в разборе обозначает бинарную операцию побитового исключающего или.
в разборе обозначает бинарную операцию побитового исключающего или.
Пусть si — xor первых i чисел на префиксе. Тогда полуинтервал (i, j] красивый если 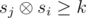 . Будем перебирать j от 1 до n. Будем рассматривать значения sj как битовые строки. На каждой итерации к ответу нам нужно прибавить величину zj — количество чисел si (i < j) таких, что
. Будем перебирать j от 1 до n. Будем рассматривать значения sj как битовые строки. На каждой итерации к ответу нам нужно прибавить величину zj — количество чисел si (i < j) таких, что 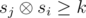 . Для этого воспользуемся структурой данных бор. Будем хранить в боре все si для i < j. Кроме самой структуры бора будем в каждой вершине хранить количество листьев в поддереве этой вершины (это легко делать при добавлении новой строки). Для вычисления значения zj будем спускаться по бору, начиная из корня. Будем накапливать число cur равное префиксу ксора числа sj с путём по которому мы спустились по бору. Пусть текущий бит в sj равен b, а i — это глубина вершины в боре в которой мы находимся. Если число cur + 2i ≥ k, то мы сразу можем прибавить к zj количество листьев вершины
. Для этого воспользуемся структурой данных бор. Будем хранить в боре все si для i < j. Кроме самой структуры бора будем в каждой вершине хранить количество листьев в поддереве этой вершины (это легко делать при добавлении новой строки). Для вычисления значения zj будем спускаться по бору, начиная из корня. Будем накапливать число cur равное префиксу ксора числа sj с путём по которому мы спустились по бору. Пусть текущий бит в sj равен b, а i — это глубина вершины в боре в которой мы находимся. Если число cur + 2i ≥ k, то мы сразу можем прибавить к zj количество листьев вершины 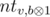 , поскольку все эти листья соответствуют si-м гарантированно дающим
, поскольку все эти листья соответствуют si-м гарантированно дающим 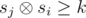 . После этого мы должны спуститься в поддерево b. Если же cur + 2i < k, то мы должны просто спуститься в поддерево
. После этого мы должны спуститься в поддерево b. Если же cur + 2i < k, то мы должны просто спуститься в поддерево  , пересчитав значение cur = cur + 2i.
, пересчитав значение cur = cur + 2i.
const int N = 1200300, LOGN = 30, V = N * LOGN;
int n, k;
int a[N];
bool read() {
if (!(cin >> n >> k)) return false;
forn(i, n) assert(scanf("%d", &a[i]) == 1);
return true;
}
int tsz;
int nt[V][2];
int cnt[V];
void clear() {
forn(i, V) {
nt[i][0] = nt[i][1] = -1;
cnt[i] = 0;
}
tsz = 1;
}
void add(int x) {
int v = 0;
cnt[v]++;
nfor(i, LOGN) {
int b = (x >> i) & 1;
if (nt[v][b] == -1) {
assert(tsz < V);
nt[v][b] = tsz++;
}
v = nt[v][b];
cnt[v]++;
}
}
int calc(int x) {
int v = 0;
int ans = 0;
auto getCnt = [](int v) { return v == -1 ? 0 : cnt[v]; };
int cur = 0;
nfor(i, LOGN) {
if (v == -1) break;
int b = (x >> i) & 1;
if ((cur | (1 << i)) >= k) {
ans += getCnt(nt[v][b ^ 1]);
v = nt[v][b];
} else {
v = nt[v][b ^ 1];
cur |= (1 << i);
}
}
if (cur >= k) ans += getCnt(v);
return ans;
}
void solve() {
clear();
add(0);
li ans = 0;
int s = 0;
forn(i, n) {
s ^= a[i];
li cur = calc(s);
ans += cur;
add(s);
}
cout << ans << endl;
}
Сложность по времени и памяти: O(nlogX), где X — наибольший из ксоров на префиксах.
Разбор этой задачи является небольшой модификацией материалов лекции, прочитанной Михаилом Тихомировым Endagorion осенью 2015-го года в МФТИ. Большое спасибо Endagorion-у за предоставленные материалы.
Легко видеть, что только числа вида p·q и p3 (для различных простых p, q) имеют ровно четыре положительных делителя.
Посчитать количество чисел вида p3 можно просто за время 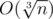 , где n — это число из условия задачи.
, где n — это число из условия задачи.
Пусть теперь p < q и π(k) — это количество простых от 1 до k. Переберём значение p. Легко видеть, что 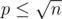 . Таким образом, для фиксированного p мы должны увеличить ответ на значение
. Таким образом, для фиксированного p мы должны увеличить ответ на значение 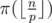 .
.
Таким образом задача свелась к подсчёту значений 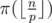 — количество простых, не превосходящих величины
— количество простых, не превосходящих величины  для всех p.
для всех p.
Введём обозначение pj — j-е простое число. Пусть dpn, j — это количество k таких, что 1 ≤ k ≤ n и все простые делители k не меньше pj (заметим, что число 1 будет учтено во всех dpn, j, поскольку оно не имеет простых делителей). dpn, j удовлетворяет реккурентному соотношению:
dpn, 1 = n (поскольку $p_1$=2).
dpn, j = dpn, j + 1 + dp⌊ n / pj⌋, j, следовательно dpn, j + 1 = dpn, j - dp⌊ n / pj⌋, j.
Пусть pk — это наименьшее простое большее  . Тогда π(n) = dpn, k + k - 1 (по определению первое слагаемое учитывает все простые не меньшие k).
. Тогда π(n) = dpn, k + k - 1 (по определению первое слагаемое учитывает все простые не меньшие k).
Если вычислять реккурентность dpn, k напрямую, то все достижимые состояния будут иметь вид dp⌊ n / i⌋, j. Также можно заметить, что если pj и pk оба больше  , то dpn, j + j = dpn, k + k. Поэтому, для всех ⌊ n / i⌋ нам достаточно хранить только
, то dpn, j + j = dpn, k + k. Поэтому, для всех ⌊ n / i⌋ нам достаточно хранить только 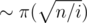 значений dp⌊ n / i⌋, j.
значений dp⌊ n / i⌋, j.
Вместо прямого подсчёта всех состояний динамики, будем осуществлять двухшаноговый процесс:
Выберем K.
Запустим рекурсивное вычисление dpn, k. Если при этом в какой-то момент мы захотим посчитать значение для состояние n < K, запомним запрос ``посчитать количество чисел не больше n с простыми делителями не меньше k''.
Посчитаем ответы на все запросы в off-line: вычислим решето для чисел до K, отсортируем все числа по наименьшему простому делителю. Теперь мы можем ответить на все запросы, используя структуру данных на прибавление в точке и взятие суммы на отрезке (например, дерево Фенвика). Запомним все ответы глобально.
Снова запустим рекурсивное вычисление dpn, j. Но в этот раз если мы захотим посчитать значение для состояния n < K, мы можем использовать уже вычисленное значение.
Эффективность этой идеи сильно зависит от величины Q — количество запросов, которые нам придётся обработать.
Утверждение. 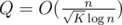 .
.
Доказательство:
Каждое состояние для предпосчёта получено из dp⌊ n / pj⌋, j переходом из большего состояния. Из этого следует, что величина Q не превосходит общего количества состояний для n > K.
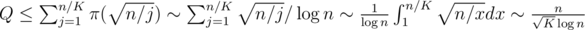
Предпосчёт ответов для Q запросов может быть выполнен за время 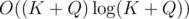 и это наиболее ёмкая часть вычислений. Выбирая оптимальным образом значение
и это наиболее ёмкая часть вычислений. Выбирая оптимальным образом значение 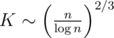 , мы получаем сложность всего решения
, мы получаем сложность всего решения 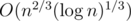 .
.
li n;
bool read() {
return !!(cin >> n);
}
const int K = 10 * 1000 * 1000;
const int N = K;
const int P = 700100;
const int Q = 25 * 1000 * 1000;
int szp, p[P];
int mind[N];
void prepare() {
szp = 0;
forn(i, N) mind[i] = -1;
fore(i, 2, N) {
if (mind[i] == -1) {
assert(szp < P);
mind[i] = szp;
p[szp++] = i;
}
for (int j = 0; j < szp && j <= mind[i] && i * p[j] < N; j++)
mind[i * p[j]] = j;
}
}
inline int getk(li n) {
int lf = 0, rg = szp - 1;
while (lf != rg) {
int md = (lf + rg) >> 1;
if (p[md] * 1ll * p[md] > n) rg = md;
else lf = md + 1;
}
assert(p[lf] * 1ll * p[lf] > n);
return lf;
}
int t[K];
void inc(int i, int val) {
for ( ; i < K; i |= i + 1)
t[i] += val;
}
int sum(int i) {
int ans = 0;
for ( ; i >= 0; i = (i & (i + 1)) - 1)
ans += t[i];
return ans;
}
int szq;
pti q[Q];
int ans[Q];
vector<int> vs[P];
void process() {
sort(q, q + szq, greater<pti> ());
memset(t, 0, sizeof(t));
forn(i, szp) vs[i].clear();
fore(i, 2, K)
vs[mind[i]].pb(i);
inc(1, +1);
int p = szp - 1;
for (int i = 0, j = 0; i < szq; i = j) {
while (p >= q[i].x) {
for (auto v : vs[p])
inc(v, +1);
p--;
}
while (j < szq && q[j].x == q[i].x) {
ans[j] = sum(q[j].y);
j++;
}
}
}
map<pair<li, int>, li> z;
li solve(li n, int jj, bool fs) {
if (!n) return 0;
int j = min(jj, getk(n));
if (!j) return n + j - jj;
li ans = 0;
if (n < K) {
pti p(j, (int) n);
if (fs) {
assert(szq < Q);
q[szq++] = p;
ans = 0;
return 0;
} else {
int idx = int(lower_bound(q, q + szq, p, greater<pti> ()) - q);
assert(idx < szq && q[idx] == p);
ans = ::ans[idx];
}
} else {
if (!z.count(mp(n, j))) {
ans = solve(n, j - 1, fs);
ans -= solve(n / p[j - 1], j - 1, fs);
z[mp(n, j)] = ans;
} else {
ans = z[mp(n, j)];
}
}
ans += j - jj;
return ans;
}
inline li pi(li n, bool fs) {
int k = szp - 1;
return solve(n, k, fs) + k - 1;
}
void solve() {
szq = 0;
z.clear();
for (int j = 0; p[j] * 1ll * p[j] <= n; j++) {
li nn = n / p[j];
if (nn > p[j]) {
pi(n / p[j], true);
}
}
process();
z.clear();
li ans = 0;
for (int j = 0; p[j] * 1ll * p[j] <= n; j++) {
li nn = n / p[j];
if (nn > p[j]) {
ans += pi(n / p[j], false);
ans -= j + 1;
}
}
for (int i = 0; i < szp && p[i] * 1ll * p[i] * 1ll * p[i] <= n; i++)
ans++;
cout << ans << endl;
}
Сложность: 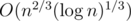 .
.
Привет, Codeforces!
Обратите внимание! Изначально тут был указан неправильный день раунда. Сейчас стоит правильная дата.
20 апреля 2016 года в 18:00 MSK состоится очередной двенадцатый учебный раунд Educational Codeforces Round 12 для участников из первого и второго дивизионов.
<Рекламное место по-прежнему свободно>
О формате и деталях проведения учебных раундов я писал уже ранее. Также об учебных раундах вы можете прочитать здесь.
Раунд будет нерейтинговым. Соревнование будет проводиться по немного расширенным правилам ACM ICPC. На решение задач у вас будет два часа. После окончания раунда будет период времени длительностью в один день, в течение которых вы можете попробовать взломать абсолютно любое решение (в том числе свое). Причем исходный код будет предоставлен не только для чтения, но и для копирования. Таким образом вы можете локально тестировать решение, которое хотите взломать, или, например, запустить стресс-тест.
Если у вас есть идеи каких-то задач, которые вам кажутся интересными, или может есть уже что-то почти готовое, что вы по каким-то причинам не можете дать на раунд (злой координатор сказал, что задача БАЯН), официальное соревнование (жюри не хочет переграбливать соревнование), можете писать мне.
Не стесняйтесь присылать как простые (и даже очень простые), так и сложные задачи (но обязательно интересные). Просьба присылать задачи к которым вы знаете решение, с понятным условием (наличие легенды исключительно по вашему желанию), а также сопровождать условия одним-двумя примерами, чтобы можно было быстро убедиться в правильности понимания условия.
</Рекламное место по-прежнему свободно>
Комплект задач был предложен участниками сообщества (пора поднимать это предложение в теги). Задачу А предложил Сергей Эрлих unprost. Задачу B прислал Ayush Anand JeanValjean01. Задачи C, D и E предложены Zi Song Yeoh zscoder (всего он прислал 10 задач так, что думаю скоро вы увидите ещё какие-то задачи из его комплекта). Sheikh Monir skmonir некоторое время назад прислал мне задачу, которая по сложности была примерно как C или D. Я решил улучшить эту задачу, значительно увеличив ограничения в ней (спасибо Михаилу Тихомирову Endagorion, который в своё время рассказал как решать подобное). Таким образом, родилась задача F.
Благодарю их и всех кто присылает задачи! Количество, присланных, но ещё не использованных задач постепенно растёт. Если я нигде ничего не потерял, то я уже ответил всем кто прислал мне задачи более 5-6 дней назад. Прошу с пониманием отнестись в случае, если ваша задача долго не появляется.
Задачи для вас подготовил я (Эдвард Давтян). Спасибо Маше Беловой Delinur за проверку английских текстов условий. Задачи вычитывали и тестировали пользователи, предложившие их, соответственно unprost, Ayush Anand JeanValjean01, Zi Song Yeoh zscoder и Sheikh Monir skmonir. Большое им за это спасибо!
На раунде вам по традиции будет предложено шесть задач. Надеюсь они вам понравятся! Думаю все задачи кроме F проще чем обычно, а вот F сложнее.
Good luck and have fun!
До финала чемпионата мира по программированию ACM ICPC осталось ровно 30 дней!
В таком месте трудно будет сосредоточиться на задачах :-)
UPD1: Первая часть соревнования закончена. Через пару минут откроются взломы. Удачи!
UPD2: Опубликован разбор задач.

Задача предложена пользователем Ali Ibrahim C137.
Заметим, что если есть пара соседних не взаимнопростых чисел, то мы обязаны между ними вставить какое-нибудь число. С другой стороны мы всегда можем вставить число 1.
const int N = 1010;
int n, a[N];
bool read() {
if (!(cin >> n)) return false;
forn(i, n) assert(scanf("%d", &a[i]) == 1);
return true;
}
void solve() {
function<int(int, int)> gcd = [&](int a, int b) { return !a ? b : gcd(b % a, a); };
vector<int> ans;
forn(i, n) {
ans.pb(a[i]);
if (i + 1 < n && gcd(a[i], a[i + 1]) > 1)
ans.pb(1);
}
cout << sz(ans) - n << endl;
forn(i, sz(ans)) {
if (i) putchar(' ');
printf("%d", ans[i]);
}
puts("");
}
Сложность: O(nlogn).
Задача предложена пользователем Srikanth Bhat bharsi.
В этой задаче нужно было сделать ровно то, что написано в условии. Никаких хитростей и подвохов.
int n, m;
bool read() {
return !!(cin >> n >> m);
}
const int N = 111;
int a[N][4];
void solve() {
forn(i, n) {
a[i][0] = 2 * i;
a[i][1] = 2 * (n + i);
a[i][2] = 2 * (n + i) + 1;
a[i][3] = 2 * i + 1;
}
vector<int> ans;
forn(i, n) {
ans.pb(a[i][1]);
ans.pb(a[i][0]);
ans.pb(a[i][2]);
ans.pb(a[i][3]);
}
nfor(i, sz(ans)) // inverse order
if (ans[i] >= m)
ans.erase(ans.begin() + i);
forn(i, m) {
if (i) putchar(' ');
printf("%d", ans[i] + 1);
}
puts("");
}
Сложность: O(n).
Задача предложена пользователем Mohammad Amin Raeisi Smaug.
Назовём отрезок [l, r] хорошим если в нём не более k ноликов. Заметим, что если отрезок [l, r] хороший, то отрезок [l + 1, r] тоже хороший. Таким образом, можно воспользоваться методом двух указателей: один указатель это l, а второй это r. Будем перебирать l слева направо и двигать r пока можем (для этого нужно просто поддерживать количество ноликов в текущем отрезке).
const int N = 1200300;
int n, k;
int a[N];
bool read() {
if (!(cin >> n >> k)) return false;
forn(i, n) assert(scanf("%d", &a[i]) == 1);
return true;
}
void solve() {
int ansl = 0, ansr = 0;
int j = 0, cnt = 0;
forn(i, n) {
if (j < i) {
j = i;
cnt = 0;
}
while (j < n) {
int ncnt = cnt + !a[j];
if (ncnt > k) break;
cnt += !a[j];
j++;
}
if (j - i > ansr - ansl)
ansl = i, ansr = j;
if (cnt > 0) cnt -= !a[i];
}
cout << ansr - ansl << endl;
fore(i, ansl, ansr) a[i] = 1;
forn(i, n) {
if (i) putchar(' ');
printf("%d", a[i]);
}
puts("");
}
Сложность: O(n).
Задачу предложена участником Sadegh Mahdavi smahdavi4.
Как известно диагонали параллелограмма делят друг друга пополам. Переберём пару точек a, b и рассмотрим середину отрезка 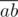 :
: 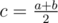 . Для всех середин отрезков посчитаем число cntc — количество пар точек, с этой серединой. Легко видеть, что ответ это
. Для всех середин отрезков посчитаем число cntc — количество пар точек, с этой серединой. Легко видеть, что ответ это 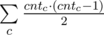 .
.
const int N = 2020;
int n;
int x[N], y[N];
bool read() {
if (!(cin >> n)) return false;
forn(i, n)
assert(scanf("%d%d", &x[i], &y[i]) == 2);
return true;
}
inline li C2(li n) { return n * (n - 1) / 2; }
void solve() {
map<pti, int> cnt;
forn(i, n)
forn(j, i) {
int cx = x[i] + x[j];
int cy = y[i] + y[j];
cnt[{cx, cy}]++;
}
li ans = 0;
for (const auto& p : cnt)
ans += C2(p.y);
cout << ans << endl;
}
Сложность: O(n2logn).
Задача предложена пользователем Lewin Gan Lewin.
Рассмотрим некоторую подпоследовательность длины k > 0 (пустые подпоследовательности можно учесть отдельно, прибавив в конце к ответу число mn) и посчитаем количество последовательностей в которых она будет учтена. Нам это нужно сделать аккуратно, чтобы всё посчитать ровно по одному разу. Пусть x1, x2, ... , xk это наша подпоследовательность. Тогда в исходной последовательности перед элементом x1 могли находиться ещё числа, но число x1 не могло встретиться (поскольку мы хотим всё посчитать по разу, варианты когда x1 уже встречалось нам не нужно учитывать). Таким образом, у нас (m - 1) вариант для каждого из чисел перед x1. Аналогичо, между числами x1 и x2 могут находиться некоторые числа (но не может находиться число x2). И так далее. После числа xk может находиться ещё некоторое количество чисел (пусть их j штук), причём на них не накладывается никаких ограничений (то есть m вариантов для каждого числа). Мы зафиксировали, что в конце стоит j чисел, значит n - k - j чисел нужно распределить между числами перед x1, между x1 и x2, \ldots , между xk - 1 и xk. Легко видеть, что это можно сделать 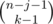 способами (это просто биномиальный коэффициент с повторениями). Количество последовательностей x1, x2, ... , xk, конечно, равно mk. Таким образом, ответ это
способами (это просто биномиальный коэффициент с повторениями). Количество последовательностей x1, x2, ... , xk, конечно, равно mk. Таким образом, ответ это 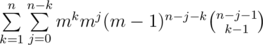 . Последнюю сумму легко преобразовать к виду
. Последнюю сумму легко преобразовать к виду 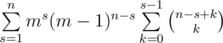 . Заметим, что последняя внутренняя сумма легко суммируется с помощью известной формулы параллельного суммирования:
. Заметим, что последняя внутренняя сумма легко суммируется с помощью известной формулы параллельного суммирования: 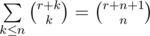 . Таким образом, ответ равен:
. Таким образом, ответ равен: 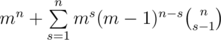 . Можно далее сворачивать сумму, чтобы получить логарифмическое решение (закнутую формулу), но в задаче это не требовалось.
. Можно далее сворачивать сумму, чтобы получить логарифмическое решение (закнутую формулу), но в задаче это не требовалось.
int n, m;
bool read() {
return !!(cin >> n >> m);
}
const int N = 1200300;
const int mod = 1000 * 1000 * 1000 + 7;
int gcd(int a, int b, int& x, int& y) {
if (!a) {
x = 0, y = 1;
return b;
}
int xx, yy, g = gcd(b % a, a, xx, yy);
x = yy - b / a * xx;
y = xx;
return g;
}
inline int inv(int a) {
int x, y;
assert(gcd(a, mod, x, y) == 1);
x %= mod;
return x < 0 ? x + mod : x;
}
inline int mul(int a, int b) { return int(a * 1ll * b % mod); }
inline int add(int a, int b) { return a + b >= mod ? a + b - mod : a + b; }
inline int sub(int a, int b) { return a - b < 0 ? a - b + mod : a - b; }
inline void inc(int& a, int b) { a = add(a, b); }
int fact[N], ifact[N];
inline int C(int n, int k) {
if (k < 0 || k > n) return 0;
return mul(fact[n], mul(ifact[k], ifact[n - k]));
}
int pm[N], pm1[N];
void solve() {
const int N = n + 1;
fact[0] = 1; fore(i, 1, N) fact[i] = mul(fact[i - 1], i);
forn(i, N) ifact[i] = inv(fact[i]);
pm[0] = 1; fore(i, 1, N) pm[i] = mul(pm[i - 1], m);
pm1[0] = 1; fore(i, 1, N) pm1[i] = mul(pm1[i - 1], sub(m, 1));
int ans = pm[n];
fore(s, 1, n + 1) {
int cur = 1;
cur = mul(cur, pm[s]);
cur = mul(cur, pm1[n - s]);
cur = mul(cur, C(n, s - 1));
inc(ans, cur);
}
cout << ans << endl;
}
Сложность: O((n + m)log MOD), где MOD = 109 + 7.
Задача предложена пользователем Kamil Debowski Errichto.
Далее приводится разбор моего решения. Также вы можете посмотреть разбор от автора задачи в английском треде.
Применим метод разделяй и властвуй. Рассмотрим отрезок [l, r] и найдём в нём подотрезок с максимальной взвешенной суммой. Для этого разобьём отрезок на две части [l, md - 1] и [md, rg], где 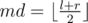 . Согласно методу разделяй и властвуй посчитаем рекурсивно ответ, если он лежит целиком в левой или правой половине. Теперь нужно учесть отрезки, пересекающие середину. Рассмотрим некоторый отрезок [i, j], i < md, md ≤ j. Взвешенная сумма на ней равна:
. Согласно методу разделяй и властвуй посчитаем рекурсивно ответ, если он лежит целиком в левой или правой половине. Теперь нужно учесть отрезки, пересекающие середину. Рассмотрим некоторый отрезок [i, j], i < md, md ≤ j. Взвешенная сумма на ней равна: 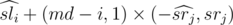 , где
, где 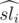 --- взвешенная сумма в подотрезке [i, md],
--- взвешенная сумма в подотрезке [i, md], 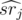 — взвешенная сумма на подотрезке [md + 1, r], а srj — просто сумма на подотрезке [md + 1, r]. Знак × применяется в смысле геометрического псевдовекторного произведения. Таким образом, у нас есть набор векторов вида (md - i, 1) и некоторый набор точек и для каждого вектора первого набора нужно найти точку из второго набора, максимизирующую значение векторного произведения. Это легко сделать, построив выпуклую оболочку по множеству точек и далее, двигая указатель по выпуклой оболочке.
— взвешенная сумма на подотрезке [md + 1, r], а srj — просто сумма на подотрезке [md + 1, r]. Знак × применяется в смысле геометрического псевдовекторного произведения. Таким образом, у нас есть набор векторов вида (md - i, 1) и некоторый набор точек и для каждого вектора первого набора нужно найти точку из второго набора, максимизирующую значение векторного произведения. Это легко сделать, построив выпуклую оболочку по множеству точек и далее, двигая указатель по выпуклой оболочке.
Обратите внимание, что в данном решении есть проблема переполнения значений векторного произведения. Эту проблему можно обойти, если сначала сравнивать значение векторного произведения в типе long double или double и только потом в типе long long. Оригинальное решение автора задачи не имеет такой проблемы.
const int N = 200200;
int n;
li a[N];
bool read() {
if (!(cin >> n)) return false;
forn(i, n) {
int x;
assert(scanf("%d", &x) == 1);
a[i] = x;
}
return true;
}
inline ptl operator- (const ptl& a, const ptl& b) { return mp(a.x - b.x, a.y - b.y); }
inline li cross(const ptl& a, const ptl& b) { return a.x * b.y - a.y * b.x; }
inline bool crossLess(const ptl& a, const ptl& b) {
ld dif = a.x * ld(b.y) - a.y * ld(b.x);
if (abs(dif) > INF) return dif <= 0;
li difl = a.x * b.y - a.y * b.x;
return difl <= 0;
}
vector<ptl> convexHull(vector<ptl> a) {
sort(all(a));
a.erase(unique(all(a)), a.end());
vector<ptl> up, dw;
forn(i, sz(a)) {
while (sz(up) > 1 && crossLess(a[i] - up.back(), up.back() - up[sz(up) - 2]))
up.pop_back();
up.pb(a[i]);
}
forn(i, sz(a)) {
while (sz(dw) > 1 && crossLess(dw.back() - dw[sz(dw) - 2], a[i] - dw.back()))
dw.pop_back();
dw.pb(a[i]);
}
reverse(all(up));
if (sz(up) > 1) dw.insert(dw.end(), up.begin() + 1, up.end() - 1);
return dw;
}
li solve(int lf, int rg) {
if (lf + 1 == rg) return a[lf];
int md = (lf + rg) >> 1;
li ans = 0;
ans = max(ans, solve(lf, md));
ans = max(ans, solve(md, rg));
vector<ptl> hull(rg - md);
li s1 = 0, s2 = 0;
fore(i, md, rg) {
s1 += (i - md + 1) * a[i];
s2 += a[i];
hull[i - md] = {-s1, s2};
}
hull = convexHull(hull);
s1 = 0, s2 = 0;
int p = 0;
for (int i = md - 1; i >= lf; i--) {
s1 += a[i];
s1 += s2;
s2 += a[i];
ptl curp(md - i, 1);
if (i == md - 1)
forn(j, sz(hull))
if (cross(curp, hull[p]) < cross(curp, hull[j]))
p = j;
while (true) {
int np = p - 1;
(np < 0) && (np += sz(hull));
if (cross(curp, hull[np]) <= cross(curp, hull[p])) break;
p = np;
}
ans = max(ans, s1 + cross(curp, hull[p]));
}
return ans;
}
void solve() {
li ans = 0;
ans = max(ans, solve(0, n));
cout << ans << endl;
}
Сложность: O(nlog2n).
Привет, Codeforces!
8 апреля 2016 года в 18:00 MSK состоится очередной одиннадцатый учебный раунд Educational Codeforces Round 11 для участников из первого и второго дивизионов.
<Изменения в последенем абзаце>
О формате и деталях проведения учебных раундов я писал уже ранее. Также об учебных раундах вы можете прочитать здесь.
Раунд будет нерейтинговым. Соревнование будет проводиться по немного расширенным правилам ACM ICPC. На решение задач у вас будет два часа. После окончания раунда будет период времени длительностью в один день, в течение которых вы можете попробовать взломать абсолютно любое решение (в том числе свое). Причем исходный код будет предоставлен не только для чтения, но и для копирования. Таким образом вы можете локально тестировать решение, которое хотите взломать, или, например, запустить стресс-тест.
Если у вас есть идеи каких-то задач, которые вам кажутся интересными, или может есть уже что-то почти готовое, что вы по каким-то причинам не можете дать на раунд (злой координатор сказал, что задача БАЯН), официальное соревнование (жюри не хочет переграбливать соревнование), можете писать мне.
Не стесняйтесь присылать как простые (и даже очень простые), так и сложные задачи (но обязательно интересные). Просьба присылать задачи к которым вы знаете решение, с понятным условием (наличие легенды исключительно по вашему желанию), а также сопровождать условия одним-двумя примерами, чтобы можно было быстро убедиться в правильности понимания условия.
</Изменения в последенем абзаце>
Комплект задач был предложен участниками сообщества. Задачу А предложил Ali Ibrahim C137. Задачу B прислал Srikanth Bhat bharsi. Задача C предложена Mohammad Amin Raeisi Smaug. Задачу D очень давно прислал Sadegh Mahdavi smahdavi4. Задача E является последней (четвёртой) из предложенных пользователем Lewin Gan Lewin. Задача F последняя (если не ошибаюсь третья) из присланных пользователем Kamil Debowski Errichto.
Благодарю их и всех кто присылает задачи! На данный момент я прочитал и ответил всем кто мне присылал задачи (кроме, возможно, присланных в течении последней недели). Надеюсь я никому не забыл ответить, все задачи у меня записаны и я о них не забываю.
Задача F подготовлена пользователем Kamil Debowski Errichto. Остальные задачи подготовил я (Эдвард Давтян). Спасибо Маше Беловой Delinur за проверку английских текстов условий. Задачи вычитывали и тестировали пользователи, предложившие их, соответственно Ali Ibrahim C137, Srikanth Bhat bharsi, Mohammad Amin Raeisi Smaug, Sadegh Mahdavi smahdavi4, Lewin Gan Lewin, Kamil Debowski Errichto. Большое им за это спасибо!
На раунде вам по традиции будут предложено шесть задач. Надеюсь они вам понравятся! В данный момент я рассматриваю возможность повторения задачи E с большими ограничениями, в качестве задачи G. Как вы смотрите на такое?
Good luck and have fun!
P.S.: Тот самый автобус из задачи B.
UPD 1: Взломы идут полным ходом. Разбор задач на русском языке готов.
UPD 2: Соревнование закончено. Поздравляю победителей tribute_to_Ukraine_2022 и uwi! Также поздравляю halyavin с победой в гонке хакеров — 93 взлома!

Задача предложена пользователем unprost.
Рассмотрим три случая.
h1 + 8a ≥ h2 — в этом случае Гусеница заберётся на яблоко тот же день, поэтому ответ равен 0.
Первое условие не выполнено и a ≤ b — в этом случае гусеница никогда не сможет забраться на яблоко, поскольку она это не сделает в первый день, а после каждой ночи она будет оказываться ниже начала прошлого дня.
Если первые два условия не выполнены, легко видеть, что ответ равен 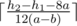 .
.
int h1, h2;
int a, b;
bool read() {
return !!(cin >> h1 >> h2 >> a >> b);
}
void solve() {
if (h1 + 8 * a >= h2)
puts("0");
else if (a > b) {
int num = h2 - h1 - 8 * a, den = 12 * (a - b);
cout << (num + den - 1) / den << endl;
} else
puts("-1");
}
Также эту задачу можно было сдать простым моделированием, поскольку высоты и скорости были небольшими.
Сложность: O(1).
Задача предложена пользователем Smaug.
Легко видеть, что для любого массива можно осуществить z-сортировку. Пусть в массиве всего 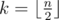 чётных позиций. Тогда можно на этих позициях расставить наибольшие k элементов массива. Очевидно после этого массив окажется z-отсортированным.
чётных позиций. Тогда можно на этих позициях расставить наибольшие k элементов массива. Очевидно после этого массив окажется z-отсортированным.
const int N = 1010;
int n, a[N];
bool read() {
if (!(cin >> n)) return false;
forn(i, n) assert(scanf("%d", &a[i]) == 1);
return true;
}
int ans[N];
void solve() {
sort(a, a + n);
int p = 0, q = n - 1;
forn(i, n)
if (i & 1) ans[i] = a[q--];
else ans[i] = a[p++];
assert(q + 1 == p);
forn(i, n) {
if (i) putchar(' ');
printf("%d", ans[i]);
}
puts("");
}
Сложность: O(nlogn).
Эта одна из задач предложенных пользователями Bayram Berdiyev bayram, Allanur Shiriyev Allanur, Bekmyrat Atayev Bekmyrat.A.
Предподсчитаем сначала для каждого числа x его позицию posx в перестановке. Это легко сделать за линейное время. Теперь рассмотрим некоторую враждебную пару (a, b) (можно считать, что posa < posb). Запомним для каждого числа a самую левую позицию posb такую, что (a, b) образуют враждебную пару. Обозначим эту величину za. Теперь будем идти по перестановке справа налево и поддерживать позицию rg наибольшего корректного интервала с левым концом в текущей позиции перестановки lf. Значение rg пересчитывается следующим образом: rg = min(rg, z[lf]). Соответсвенно к ответу на каждой итерации нужно прибавлять величину rg - lf + 1.
const int N = 300300;
int n, m;
int p[N];
pt b[N];
bool read() {
if (!(cin >> n >> m)) return false;
forn(i, n) {
assert(scanf("%d", &p[i]) == 1);
p[i]--;
}
forn(i, m) {
int x, y;
assert(scanf("%d%d", &x, &y) == 2);
x--, y--;
b[i] = pt(x, y);
}
return true;
}
int pos[N];
vector<int> z[N];
void solve() {
forn(i, n) pos[p[i]] = i;
forn(i, n) z[i].clear();
forn(i, m) {
int x = pos[b[i].x], y = pos[b[i].y];
if (x > y) swap(x, y);
z[x].pb(y);
}
li ans = 0;
int rg = n;
nfor(i, n) {
forn(j, sz(z[i])) rg = min(rg, z[i][j]);
ans += rg - i;
}
cout << ans << endl;
}
Сложность: O(n + m).
Задачу предложил Алексей Дергунов dalex.
Эта задача является стандартной двумерной задачей, которая решается с помощью одномерной структуры данных. Абсолютно аналогично решаются многие другие задачи (например, поиск наибольшей по весу цепочки точек на плоскости такой, что у каждой следующей точки обе координаты больше, чем у предыдущей). Запишем задачу формально для всех i нам нужно посчитать, количество индексов j, что выполнены следующие условия: ai < aj и bj < aj. Отсортируем все отрезки по левому концу справа налево. И в некоторой структуре данных (удобнее всего здесь использовать дерево Фенвика) будем поддерживать правые концы уже обработанных отрезков (с большим левым концом, чем у текущего отрезка). Тогда для текущего отрезка ответом является сумма на префиксе его правого конца.
Таким образом, от одной размерности задачи (от условия ai < aj) мы избавились с помощью сортировки и обработки отрезков справа налево. А от второй размерности (условия bj < aj) мы избавились использованием структуры данных (взятием суммы на префиксе).
const int N = 1200300;
int n;
pair<pti, int> a[N];
bool read() {
if (!(cin >> n)) return false;
forn(i, n) assert(scanf("%d%d", &a[i].x.x, &a[i].x.y) == 2), a[i].y = i;
return true;
}
int t[N];
vector<int> ys;
inline void inc(int i, int val) {
for ( ; i < sz(ys); i |= i + 1)
t[i] += val;
}
inline int sum(int i) {
int ans = 0;
for ( ; i >= 0; i = (i & (i + 1)) - 1)
ans += t[i];
return ans;
}
int ans[N];
void solve() {
ys.clear();
forn(i, n) ys.pb(a[i].x.y);
sort(all(ys));
ys.erase(unique(all(ys)), ys.end());
forn(i, sz(ys)) t[i] = 0;
sort(a, a + n);
nfor(i, n) {
int idx = int(lower_bound(all(ys), a[i].x.y) - ys.begin());
ans[a[i].y] = sum(idx);
inc(idx, +1);
}
forn(i, n) printf("%dn", ans[i]);
}
Сложность: O(nlogn).
Задачу предложил Алексей Дергунов dalex.
Компонентой рёберной двусвязности в неориентированном графе называется наибольшее по включению множество вершин такой, что между любой парой вершин существует два рёберно-неперескающихся пути. Рассмотрим граф в котором вершинами являются компоненты рёберной двусвязности исходного графа. Легко видеть, что этот граф является деревом (если бы в нём был цикл, то компоненты цикла образовывали бы одну компоненту двусвязности). Поскольку рёбра исходного графа разрушаются после прохождения по ним, мы не можем перейдя по ребру этого дерева вернуться назад (поскольку это дерево).
Рассмотрим компоненты двусвязности в которые попали вершины a и b. Обозначим их A и B. Утверждение: ответ YES если и только, если на пути в дереве между вершинами A и B либо есть ребро дерева с артефактом, либо есть компонента содержащая внутри себя ребро с артефактом. Легко видеть, что утверждение верно: если такое ребро есть, то мы либо пройдём по нему пока будем идти по дереву из A в B, либо можем пройти по нему внутри компоненты (ведь внутри компоненты между каждой парой вершин есть два рёберно-непересекающихся пути). Обратное также легко непосредственно проверить.
Одним из способов выделить компоненты рёберной двусвязнсти является следующий:
Ориентируем исходный неориентированный граф по обходу в глубину (для каждого ребра запомним в каком направлении мы впервые захотели пройти по нему).
Выделим в этом ориентированном графе компоненты сильной связности.
Утверждение: компоненты сильной связности нового графа будут совпадать с компоненты рёберной двусвязности исходного графа.
Также в этой задаче можно было заметить, что рёбрами дерева будут мосты (мосты в смысле теории графов, а не легенды из условия). Поэтому для решения задачи достаточно выделить мосты в графе.
const int N = 500500, M = 500500;
int n, m;
int eused[M];
vector<int> eid[N];
vector<int> g1[N], tg1[N];
vector<int> w[N];
int a, b;
bool read() {
if (!(cin >> n >> m)) return false;
forn(i, m) eused[i] = false;
forn(i, n) {
g1[i].clear();
tg1[i].clear();
eid[i].clear();
w[i].clear();
}
forn(i, m) {
int x, y, z;
assert(scanf("%d%d%d", &x, &y, &z) == 3);
x--, y--;
g1[x].pb(y);
g1[y].pb(x);
eid[x].pb(i);
eid[y].pb(i);
w[x].pb(z);
w[y].pb(z);
}
assert(cin >> a >> b);
a--, b--;
return true;
}
int u, used[N];
int sz, perm[N];
void dfs1(int v) {
used[v] = u;
forn(i, sz(g1[v])) {
int u = g1[v][i];
int cid = eid[v][i];
if (!eused[cid]) {
eused[cid] = true;
tg1[u].pb(v);
}
if (used[u] != ::u)
dfs1(u);
}
perm[sz++] = v;
}
int c, comp[N];
void dfs2(int v) {
used[v] = u;
for (auto u : tg1[v]) if (used[u] != ::u) dfs2(u);
comp[v] = c;
}
vector<int> g2[N];
vector<int> w2[N];
bool good[N];
bool dfs3(int v, int p, int t, bool& ans) {
if (v == t) {
ans |= good[v];
return true;
}
forn(i, sz(g2[v])) {
int to = g2[v][i];
if (to == p) continue;
if (dfs3(to, v, t, ans)) {
ans |= good[v];
ans |= w2[v][i];
return true;
}
}
return false;
}
void solve() {
u++, sz = 0;
dfs1(0);
assert(sz == n);
reverse(perm, perm + sz);
u++, c = 0;
forn(i, sz) if (used[perm[i]] != u) dfs2(perm[i]), c++;
forn(i, c) good[i] = false;
forn(i, c) {
g2[i].clear();
w2[i].clear();
}
forn(i, n)
forn(j, sz(g1[i])) {
int x = comp[i], y = comp[g1[i][j]];
if (x != y) {
g2[x].pb(y);
w2[x].pb(w[i][j]);
} else if (w[i][j]) good[x] = true;
}
n = c;
a = comp[a], b = comp[b];
bool ans = good[a];
assert(dfs3(a, -1, b, ans));
puts(ans ? "YES" : "NO");
}
Сложность: O(n + m).
Задача предложена пользователем Lewin Gan Lewin.
Наблюдение 1: если для нас муравьи неразличимы, можно считать, что никаких столкновений не происходит, а муравьи просто проходят друг через друга. Таким образом, мы можем легко узнать положения всех муравьёв в конце, но мы не можем сказать какой муравей где находится.
Наблюдение 2: относительный порядок муравьёв никогда не меняется.
Таким образом для решения задачи нам достаточно определить положения хотя бы одного муравья по прошествии t единиц времени.
Будем решать эту задачу следующим образом:
Рассмотрим положения муравьёв по прошествии m единиц времени. Легко видеть согласно первого наблюдения, что положения муравьёв остнутся исходными, но порядок изменится (произойдёт циклический сдвиг порядка). Найдём этот циклический сдвиг sh и применим его 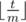 раз.
раз.
После этого останется 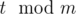 единиц времени.
единиц времени.
Таким образом, задача свелась к тому, чтобы промоделировать процесс для одного муравья за время m и за время 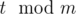 . Заметим, что за промежуток времени не больший m один фиксированный муравей не может столкнуться с другим муравьём более двух раз. Таким образом, если мы будем игнорировать столкновения всех остальных муравьёв кроме фиксированного всего произойдёт не более 2n столкновений.
. Заметим, что за промежуток времени не больший m один фиксированный муравей не может столкнуться с другим муравьём более двух раз. Таким образом, если мы будем игнорировать столкновения всех остальных муравьёв кроме фиксированного всего произойдёт не более 2n столкновений.
Давайте моделировать этот процесс с помощью двух очередей муравьёв идущих влево и вправо. Каждый раз мы должны брать в очереди противоположного направления первого муравья, обрабатывать столкновение и кидать его в конец очереди другого направления.
Подсказка: если у вас возникнут проблемы со случаем, когда муравей может попасть в две позиции, просто промоделируйте процес со следующим муравьём.
const int N = 300300;
int n, m;
li t;
pair<pair<int, char>, int> a[N];
bool read() {
if (!(cin >> n >> m >> t)) return false;
forn(i, n) {
assert(scanf("%d %c", &a[i].x.x, &a[i].x.y) == 2);
a[i].x.x--;
a[i].y = i;
}
return true;
}
int dx[] = { -1, +1 };
const string dirs("LR");
inline int getDir(char d) { return (int) dirs.find(d); }
inline int getPos(li x, char d, li t) {
x %= m, t %= m;
li ans = (x + t * dx[getDir(d)]) % m;
(ans < 0) && (ans += m);
return int(ans);
}
typedef pair<li, li> ptl;
void clear(queue<ptl>& q) { while (!q.empty()) q.pop(); }
queue<ptl> tol, tor;
int calc(int v, li t) {
clear(tol);
clear(tor);
fore(d, 1, n) {
int i = (v - d + n) % n;
if (a[i].x.y == 'R') tor.push(mp(i > v ? a[i].x.x - m : a[i].x.x, 0));
}
fore(d, 1, n) {
int i = (v + d) % n;
if (a[i].x.y == 'L') tol.push(mp(i < v ? a[i].x.x + m : a[i].x.x, 0));
}
li cx = a[v].x.x;
char cd = a[v].x.y;
li curt = 0;
while (t > 0) {
if (cd == 'R') {
if (tol.empty()) return getPos(cx, cd, t);
assert(curt >= tol.front().y);
li nx = tol.front().x - (curt - tol.front().y);
tol.pop();
li d = min((nx - cx + 1) >> 1, t);
assert(cx <= nx);
cx += d, nx -= d;
t -= d;
if (cx > nx) {
assert((nx - cx) & 1);
cx--, nx++;
}
assert(cx <= nx);
cd = 'L';
curt += d;
assert(nx - m < cx);
tor.push(mp(nx - m, curt));
} else {
if (tor.empty()) return getPos(cx, cd, t);
assert(curt >= tor.front().y);
li nx = tor.front().x + (curt - tor.front().y);
tor.pop();
li d = min((cx - nx + 1) >> 1, t);
assert(cx >= nx);
cx -= d, nx += d;
t -= d;
if (cx < nx) {
assert((cx - nx) & 1);
cx++, nx--;
}
assert(cx >= nx);
cd = 'R';
curt += d;
assert(nx + m > cx);
tol.push(mp(nx + m, curt));
}
}
return getPos(cx, cd, 0);
}
int ans[N];
void solve() {
assert(n > 1);
sort(a, a + n);
vector<int> poss;
forn(i, n)
poss.pb(getPos(a[i].x.x, a[i].x.y, t));
sort(all(poss));
vector<vector<int>> xs;
forn(s, 2) {
int x = calc(s, m);
int pos = -1;
forn(i, n)
if (a[i].x.x == x) {
assert(pos == -1);
pos = i;
}
assert(pos != -1);
pos = (pos - s + n) % n;
li k = (t / m) % n;
pos = int((s + pos * k) % n);
x = calc(pos, t % m);
xs.pb(vector<int>());
forn(i, sz(poss))
if (poss[i] == x)
xs.back().pb(i);
assert(!xs.back().empty());
if (sz(xs.back()) == 2) assert(xs.back()[0] + 1 == xs.back()[1]);
}
int pos = xs[0][0];
if (sz(xs[0]) > 1) {
assert(sz(xs[0]) == 2);
assert(pos + 1 == xs[0][1]);
if (xs[0] != xs[1])
pos = xs[0][1];
}
forn(ii, n) {
int i = (ii + pos) % sz(poss);
ans[a[ii].y] = poss[i];
}
forn(i, n) {
if (i) putchar(' ');
assert(0 <= ans[i] && ans[i] < m);
printf("%d", ans[i] + 1);
}
puts("");
}
Сложность: O(nlogn).
Привет, Codeforces!
25 марта 2016 года в 16:00 MSK после продолжительного перерыва состоится очередной десятый учебный раунд Educational Codeforces Round 10 для участников из первого и второго дивизионов. Перерыв, конечно же, связан с большой плотностью соревнований и чемпионатов на Codeforces.
<То же, что и было раньше>
О формате и деталях проведения учебных раундов я писал уже ранее. Также об учебных раундах вы можете прочитать здесь.
Раунд будет нерейтинговым. Соревнование будет проводиться по немного расширенным правилам ACM ICPC. На решение задач у вас будет два часа. После окончания раунда будет период времени длительностью в один день, в течение которых вы можете попробовать взломать абсолютно любое решение (в том числе свое). Причем исходный код будет предоставлен не только для чтения, но и для копирования. Таким образом вы можете локально тестировать решение, которое хотите взломать, или, например, запустить стресс-тест.
Если у вас есть идеи каких-то задач, которые вам кажутся интересными, или может есть уже что-то почти готовое, что вы по каким-то причинам не можете дать на раунд (злой координатор сказал, что задача БАЯН), официальное соревнование (жюри не хочет переграбливать соревнование), можете писать мне.
Не стесняйтесь присылать простые (и даже очень простые) задачи (но обязательно интересные). Почти каждый раунд достаточно быстро выбираются кандидаты для задач C, D, E, F, а вот задача A обычно ставится самой последней, когда уже почти всё готово.
</То же, что и было раньше>
Теперь уже традиционно комплект задач был полностью предложен участниками сообщества. Задачу А уже в третий раз предложил пользователь unprost (ну сами понимаете не стоит ждать короткого условия :-)). Задачу B прислал пользователь Smaug. Задача C — ещё одна задача из комплекта, который прислали Bayram Berdiyev bayram, Allanur Shiriyev Allanur, Bekmyrat Atayev Bekmyrat.A. Задачи D и E были предложены Алексеем Дергуновым dalex. Задачу F ещё давно прислал Lewin Gan Lewin.
Благодарю их и всех кто присылает задачи или просто наброски!
Задачи D и E были подготовлены Алексеем Дергуновым dalex. Остальные задачи подготовил я (Эдвард Давтян). Хочу отметить генератор тестов по задаче E, который я писал примерно столько же, сколько решение задачи F. Спасибо Маше Беловой Delinur за проверку английских текстов условий. Задачи тестировали пользователи unprost, Smaug, Aleksa Plavsic allllekssssa, Алексей Дергунов dalex и Lewin Gan Lewin. Большое им за это спасибо!
На раунде вам по традиции будут предложено шесть задач. Надеюсь они вам понравятся!
P.S.: Мне очень нравится задача F, надеюсь увидеть Accepted-ы по ней.
Good luck and have fun!
UPD: Соревнование закончено. Разбор задач готов.

Задача предложена пользователем unprost.
Рассмотрим на процесс с конца. Последний покупатель всегда покупает половину яблока и половину получает бесплатно (поэтому последняя строка на самом деле всегда равна halfplus). Далее каждый покупатель удваивает текущее количество яблок и возможно прибавляет к нему единицу. Таким образом, нам просто задано бинарное представление числа записанное с конца. Для подсчёта ответа нужно просто с конца восстанавливать количество яблок попутно, вычисляя сумму денег.
С++ solution by me.
С++ solution by unprost.
Сложность: O(p).
Задача предложена пользователем Lewin Gan Lewin.
Посчитаем частичные суммы на префиксах отдельно для всех чисел (в массиве s1) и отдельно для чисел напротив, которых стоит буква B (в массиве s2). Теперь мы можем за O(1) вычислять сумму на любом подотрезке, а также сумму на любом отрезке по числам напротив буквы B.
Переберем теперь префикс или суффикс и посчитаем сумму в случае его изменения по формуле: sum(s1, 0, n - 1) + sum(s2, 0, i) - 2·sum(s1, 0, i) для префикса и sum(s1, 0, n - 1) + sum(s2, i, n - 1) - 2·sum(s1, i, n - 1) для суффикса.
C++ solution by me.
Python solution by Lewin.
Сложность: O(n).
Задача предложена пользователем Lewin Gan Lewin. Доказательство транзитивности также принадлежит ему.
Отсортируем все строки по компаратору a + b < b + a и сконкатенируем их в получившемся порядке. Докажем, что ответ оптимальный. Пусть эта операция транзитивна (то есть из 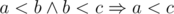 ). Рассмотрим оптимальный ответ в котором есть пара строк, находящихся по этому отношению в обратном порядке. Поскольку это отношение транзитивно, то без потери общности можно считать, что это пара соседних строк. Но тогда мы их можем просто поменять местами и улучшить ответ.
). Рассмотрим оптимальный ответ в котором есть пара строк, находящихся по этому отношению в обратном порядке. Поскольку это отношение транзитивно, то без потери общности можно считать, что это пара соседних строк. Но тогда мы их можем просто поменять местами и улучшить ответ.
Докажем транзитивность отношения. Будем смотреть на эти строки как на числа в 26-ной системе счисления. Тогда отношения a + b < b + a эквивалентно 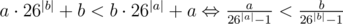 . Последнее есть просто отношение для действительных чисел. Таким образом, мы доказали транзитивность отношения a + b < b + a.
. Последнее есть просто отношение для действительных чисел. Таким образом, мы доказали транзитивность отношения a + b < b + a.
C++ solution by me.
Python solution by Lewin.
Сложность: O(nLlogn), где L — наибольшая длина строки.
Задачу предложил Денис Безруков pitfall.
Пусть cntx количество повторений числа x в заданном массиве (понятно, что числа большие m можно не рассматривать). Переберём  и 1 ≤ k, x·k ≤ m и увеличим значение в позиции k·x в некотором массиве z на величину cntx. Таким образом, значение zl равно количеству чисел в исходном массиве делящих l. Найдём минимальное l с максимальным значением zl (1 ≤ l ≤ m). Легко видеть, что ответом на задачу будут числа делящие l.
и 1 ≤ k, x·k ≤ m и увеличим значение в позиции k·x в некотором массиве z на величину cntx. Таким образом, значение zl равно количеству чисел в исходном массиве делящих l. Найдём минимальное l с максимальным значением zl (1 ≤ l ≤ m). Легко видеть, что ответом на задачу будут числа делящие l.
Оценим время работы решения. Количество пар (k, x) можно сверху оценить как 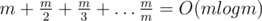 .
.
C++ solution by me.
Java solution by pitfall.
Сложность: O(n + mlogm).
Задачу предложил Алексей Чесноков CleRIC.
Пусть k = 2, тогда это стандартная задача которая может быть решена с помощью БПФ (быстрого преобразования Фурье). А решается она следующим образом: рассмотрим многочлен в которого коэффициент при i-й степени равен единице если и только если в заданном массиве есть число i. Возведём этот многочлен в квадрат, тогда те i коэффициент при которых в квадрате не равен 0 будут находиться в ответе. Легко обобщить это решение на случай произвольного k. Нужно просто исходный многочлен возвести в k-ю степень. Это, конечно, нужно сделать с помощью бинарного возведения в степень. Сложность получается O(WlogWlogk), где W — максимальная сумма.
Заметим, что это решение можно улучшить. Зачем возводить в степень многочлен, когда можно возводить в степень его образ (то есть его ДПФ)? Единственное, что нас может остановить это то, что в случае комплексного БПФ будут получаться очень большие числа (порядка 1000-х степеней) и соответственно никакие вещественные типа нас не спасут). Но это можно сделать в целых числах используя теоретикочисловое преобразование Фурье (ТПФ). У этого решения есть проблема, что при преобразовании (прямом или обратном) какие-то коэффициенты могут случайно обнулиться по модулю простого из ТПФ, но на самом деле коэффициент не ноль. Это можно обойти случайным выбором простого (а лучше двух или трёх), чтобы никто не мог взломать решение. Таким образом, получаем сложность O(W(logW + logk)).
Основное авторское решение было со сложностью O(WlogWlogk) с комплексным Фурье, второе с той же сложностью но по модулю, третье было с улучшенной асимптотикой (решение уже взломано Андреем Халявиным halyavin).
С++ solution, complex FFT by me.
С++ solution, NTT by me.
С++ solution, improved NTT by me.
С++ solution by CleRIC.
P.S.: Чтобы решение было быстрым нужно каждый раз умножать многочлены нужной степени, а не степени 220.
Сложность: O(WlogWlogk) или O(W(logW + logk)), в зависимости от смелости кодера :-)
UPD: Оказывается первый подход тоже имеет сложность O(W(logW + logk)). Смотри ниже комментарий пользователя halyavin.
Задача предложена пользователем Lewin Gan Lewin. Решение и доказательство также принадлежат ему.
Рассмотрим полный граф с весами рёбер aij. Обозначим Bij — минимальное значение максимального ребра на пути из вершины i в вершину j. Очевидно aij ≥ Bij по определение Bij.
Если матрица волшебная мы можем выбрать произвольную последовательность k1, k2, ..., km и получить aij ≤ max{ai, k1, ak1, k2, ..., akm, j} (для этого нужно последовательно применить третье неравенство для волшебной матрицы). Также легко показать, что если это условие выполнено, то матрицы волшебная (нужно просто взять m = 1 и выбрать произвольное k1).
Таким образом, мы получили, что матрица волшебная тогда и только тогда, когда aij ≤ Bij. Пользуясь неравенством aij ≥ Bij окончательно получаем ai, j = Bi, j.
Теперь нам нужно быстрый способ подсчёта значений Bij для всех пар (i, j). Это можно сделать вычислым MST (минимальное покрывающее дерево графа), поскольку MST минимизирует максимальное ребро на путях между всеми парами вершин. Таким образом, решение выглядит следующим образом: сначала нужно найти MST (например, алгоритмом Прима за O(n2)), а затем нужно найти наибольшее ребро на пути из i в j и проверить, что оно равно aij (я это делал с помощью бинарного подъёма по дереву, но это можно делать во время построения MST). И, конечно, нужно не забыть предварительно проверить матрицу на симметричность и нули на диагонали.
P.S.: К сожалению в этой задаче мы не могли увеличить n, поскольку тесты здесь очень специфические (и уже имели размер порядка 67MB) и генератором их задавать было нельзя. Большинство решений, которые сдали участники на контесте использует bitset-ы и работает за  , где b = 32 или b = 64.
, где b = 32 или b = 64.
C++ solution, binary lifts by me.
Java solution by Lewin.
Сложность: O(n2logn) или O(n2).
Привет, Codeforces!
Поздравляю всех с наступлением весны!

01 марта 2016 года в 18:00 MSK состоится девятый учебный раунд Educational Codeforces Round 9 для участников из первого и второго дивизионов. Снова отмечаю плотность соревнований и чемпионатов в эти дни и надеюсь, что она вас не спугнёт и вы напишете ER9.
<В этот раз я ничего тут не менял>
О формате и деталях проведения учебных раундов я писал уже ранее. Также об учебных раундах вы можете прочитать здесь.
Раунд будет нерейтинговым. Соревнование будет проводиться по немного расширенным правилам ACM ICPC. На решение задач у вас будет два часа. После окончания раунда будет период времени длительностью в один день, в течение которых вы можете попробовать взломать абсолютно любое решение (в том числе свое). Причем исходный код будет предоставлен не только для чтения, но и для копирования. Таким образом вы можете локально тестировать решение, которое хотите взломать, или, например, запустить стресс-тест.
Если у вас есть идеи каких-то задач, которые вам кажутся интересными, или может есть уже что-то почти готовое, что вы по каким-то причинам не можете дать на раунд (злой координатор сказал, что задача БАЯН), официальное соревнование (жюри не хочет переграбливать соревнование), можете писать мне.
Не стесняйтесь присылать простые (и даже очень простые) задачи (но обязательно интересные). Почти каждый раунд достаточно быстро выбираются кандидаты для задач C, D, E, F, а вот задача A обычно ставится самой последней, когда уже почти всё готово.
</В этот раз я ничего тут не менял>
Снова комплект задач был полностью предложен участниками сообщества. Задача А как и в прошлый раз была предложена пользователем unprost (будьте готовы к длинному условию). Задачу D предложил Денис Безруков pitfall. Задачу E достаточно давно прислал Алексей Чесноков CleRIC. Задачи B, C и F были предложены пользователем Lewin Gan Lewin.
Благодарю их и всех кто присылает задачи или просто наброски!
Подготовкой задач занимался я (Эдвард Давтян). Спасибо Маше Беловой Delinur за проверку английских текстов условий. Тестерами задач выступили те кто их предложили: unprost, Алексей Чесноков CleRIC и Lewin Gan Lewin. Большое им за это спасибо!
На раунде вам по традиции будут предложено шесть задач. Надеюсь они вам понравятся!
Good luck and have fun!
UPD1: Первая часть соревнования завершена. Можете взламывать другие решения.
UPD2: В связи с техническими проблемами фаза открытых взломов будет открыта позже (через несколько часов).
UPD3: Разбор задач на русском языке готов.
UPD4: Соревнование закончено. Системное тестирование начнётся через несколько минут.
UPD5: Лучшие три взломщика:
P_Nyagolov — 31 взлом
khadaev — 27 взломов
halyavin — 23 взлома
Задача предложена пользователем unprost.
В этой задаче можно было просто промоделировать процесс. А можно было заметить, что после каждого матча один игрок выбывает. Всего выбывших n - 1. Таким образом, всего нам нужно (n - 1) * (2b + 1) бутылок воды. Полотенец, конечно, нам нужно np штук.
Сложность: O(log2n), O(logn) или O(1) в зависимости от реализации.
Эта одна из задач предложенных пользователями Bayram Berdiyev bayram, Allanur Shiriyev Allanur, Bekmyrat Atayev Bekmyrat.A.
Ключевым для решения задачи является наблюдение, что число делится на 4 тогда и только тогда, когда его последние две цифры делятся на 4. Таким образом, для подсчёта ответа достаточно сначала посчитать количество подстрок длины один. Далее нужно рассмотреть пары соседних цифр таких, что они образуют двузначное число кратное 4-м и прибавить к ответу индекс правого из них.
Сложность: O(n).
Задачи предложена и подготовлена Камилем Дебовски Errichto.
В этой задаче можно действовать жадно. Будем идти по строке слева направо. Рассмотрим наибольшее расстояние d, которое мы можем получить на этой позиции (это либо расстояние вниз до буквы 'a', либо вверх до буквы 'z'). Пусть v = min(d, k). Поставим на текущей позиции букву на расстоянии v (вниз или вверх), а значение k уменьшим на v. Если после обработки всей строки, k оказалось больше нуля, то ответа не существует. В противном случае мы нашли ответ.
Сложность: O(n).
Более простую версию задачи предложил Kareem Mohamed Kareem_Mohamed.
Обозначим ответ на задачу как f(a, b). Заметим, что f(a, b) = f(0, b) - f(0, a - 1) или что то же самое f(a, b) = f(0, b) - f(0, a) + g(a), где g(a) равно единице если a является волшебным число, иначе g(a) равно нулю. Далее будем решать задачу для отрезка [0, n].
Далее приводится стандартная техника, которую иногда называют 'динамикой по цифрам'. Её можно реализовать двумя способами, в первом перебирается длина префикса числа, который совпадёт с префиксом числа n. Следующий символ может быть произвольным меньшим соответствующей цифры в n, а далее любые цифры. Но я расскажу о втором подходе.
Пусть zijk равно количеству волшебных префиксов длины i, дающих остаток j при делении на m. При этом если k = 0, то префикс должен быть строго меньше префикса числа n, а если k = 1, то префикс должен быть равен префиксу числа n (больше он быть не может). Будем делать динамику вперёд. Переберём цифру 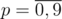 , которую мы поставим на позиции i. При этом нам нужно проверить, что если позиция чётна то эта цифра должна быть равна d, а в противном случае она не может быть равна d. Также нужно проверить, что если k = 1, то эта цифра не может быть больше соответствующей цифры в числе n. Теперь поймём в какое состояние мы попадём после такого перехода. Конечно, i' = i + 1. Согласно схеме Горнера j' = (10j + p) mod m. Легко видеть, что
, которую мы поставим на позиции i. При этом нам нужно проверить, что если позиция чётна то эта цифра должна быть равна d, а в противном случае она не может быть равна d. Также нужно проверить, что если k = 1, то эта цифра не может быть больше соответствующей цифры в числе n. Теперь поймём в какое состояние мы попадём после такого перехода. Конечно, i' = i + 1. Согласно схеме Горнера j' = (10j + p) mod m. Легко видеть, что 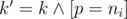 . Для перехода нужно сделать zi'j'k' + = zijk. Конечно, нужно не забыть делать все операции по модулю 109 + 7.
. Для перехода нужно сделать zi'j'k' + = zijk. Конечно, нужно не забыть делать все операции по модулю 109 + 7.
Сложность: O(nm).
Задача предложена Ali Ahmadi Kuzey.
Давайте сначала сделаем предподсчёт zlij, zrij, zldij — наибольшее количество букв 'z' влево, вправо и влево-вниз от позиции (i, j). Это легко сделать за O(nm). Пусть мы зафиксировали некоторую клетку (i, j). Рассмотрим величину c = min(zlij, zldij). Это наибольший допустимый размер квадрата с верхним правым углом в (i, j). Теперь поймём сколько таких квадратов. Рассмотрим произвольную клетку (x, y) по диагонали вниз-влево на расстоянии не более c. Пара клеток (i, j) и (x, y) образует z-паттерн, если y + zrxy > j.
Отлично, теперь для решения задачи заведём структуру данных для каждой диагонали (она определяется формулой x + y), которая умеет прибавлять в точке и брать сумму на отрезке (лучше всего для этого подходит дерево Фенвика). Будем перебирать столбец j справа налево и обрабатывать события: некоторая клетка (x, y) такова, что y + zrxy - 1 = j. В этом случае нам нужно в дереве номер x + y сделать прибавление в точке y на единицу. Теперь будем перебирать клетку в текущем столбце (i, j). Тогда к ответу нужно прибавить величину суммы в дереве номер i + j на отрезке от j - c + 1 до j.
Сложность: O(nmlogm).
Задача предложена и подготовлена Камилем Дебовски Errichto.
Вначале для удобства добавим подсказку с upTo = b, quantity = n, а затем отсортируем подсказки по значению upTo. Отсортированные подсказки разбивают интервал [1, b] на q непересекающихся промежутка. Для каждого промежутка мы знаем количество элементов в нём.
Для решения задачи построим сеть (описанную ниже) и найдём в ней максимальный поток. Ответ fair только если величина потока равна n.
Соединим каждую вершину из A с истоком ребром пропускной способности  . Каждую вершину из B соединим со стоком ребром пропускной способности равной количеству чисел в этом промежутке. Между всему вершинами x из A и y из B добавим ребро пропускной способности равной количеству чисел в промежутке с остатком x в промежутке y.
. Каждую вершину из B соединим со стоком ребром пропускной способности равной количеству чисел в этом промежутке. Между всему вершинами x из A и y из B добавим ребро пропускной способности равной количеству чисел в промежутке с остатком x в промежутке y.
Легко видеть, что поток в данной сети очень похож на паросочетание. В самом деле мы можем воспользоваться теоремой Холла. Для каждого из 25 множеств вершин из A (множества остатков) пройдём по всем промежуткам и посчитаем количество чисел, которые мы можем взять в [1, b] с остатками в заданном множестве.
Реализицая с теоремой Холла: C++ solution.
Сложность: O(2Cn), где в нашей задаче C = 5.
Привет, Codeforces!
19 февраля 2016 года в 18:00 MSK состоится восьмой учебный раунд Educational Codeforces Round 8 для участников из первого и второго дивизионов. Надеюсь плотность контестов на Codeforces в эти несколько дней вас не спугнёт и вы напишете ER8.
<В конце добавилась фраза про простые задачи>
О формате и деталях проведения учебных раундов я писал уже ранее. Также об учебных раундах вы можете прочитать здесь.
Раунд будет нерейтинговым. Соревнование будет проводиться по немного расширенным правилам ACM ICPC. На решение задач у вас будет два часа. После окончания раунда будет период времени длительностью в один день, в течение которых вы можете попробовать взломать абсолютно любое решение (в том числе свое). Причем исходный код будет предоставлен не только для чтения, но и для копирования. Таким образом вы можете локально тестировать решение, которое хотите взломать, или, например, запустить стресс-тест.
Если у вас есть идеи каких-то задач, которые вам кажутся интересными, или может есть уже что-то почти готовое, что вы по каким-то причинам не можете дать на раунд (злой координатор сказал, что задача БАЯН), официальное соревнование (жюри не хочет переграбливать соревнование), можете писать мне.
Не стесняйтесь присылать простые (и даже очень простые) задачи (но обязательно интересные). Почти каждый раунд достаточно быстро выбираются кандидаты для задач C, D, E, F, а вот задача A обычно ставится самой последней, когда уже почти всё готово.
</В конце добавилась фраза про простые задачи>
В этот раз, впервые, полностью комплект задач был предложен участниками сообщества. Задача А была предложена пользователем unprost. Задача B взята из комплекта, который прислали Bayram Berdiyev bayram, Allanur Shiriyev Allanur, Bekmyrat Atayev Bekmyrat.A. Задачу D предложил Kareem Mohamed Kareem_Mohamed (я её правда сильно усложнил, чтобы вам было интереснее :-)). Задачу E прислал Ali Ahmadi Kuzey. Задачи C и F были предложены Камилом Дебовски Errichto.
Благодарю их и всех кто присылает задачи или просто наброски!
Подготовкой задач в этот раз занимался не только я (Эдвард Давтян). Большое спасибо Камилу Дебовски Errichto, который не только предложил задачи C и F, но и подготовил их. Спасибо Маше Беловой Delinur за проверку английских текстов условий. Также большое спасибо Ali Ahmadi Kuzey, который помогал с тестированием задач.
На этом раунде вам по традиции будет предложено шесть задач.
Вкратце опишу задачи: A) Простая задача с немаленьким условием; B) Надеюсь вы не будете здесь писать ничего сложного; C) Интересная; D) Немного техническая, содержит очень полезную технику; E) Мне эта задача очень нравится; F) Супер клёвая задача, если не удастся сдать на контесте рекомендую дорешать.
Good luck and have fun!
UPD1: Первая фаза соревнования закончена. Начались взломы. Разбор задач готов.
Поскольку все задачи Errichto про медведей ниже находится иллюстрация к задаче C (Limak кажется первый слева):

Вычтем из числа n единицу. Определим сначала номер блока в который попало n-е число. Для это сначала вычтем из числа n число 1, затем 2, затем 3 и так далее пока n не станет отрицательным. Количество вычитаний и будем номером блока, а позицией в блоке будет последнее неотрицательное число, которое мы встретим.
Сложность:  .
.
В этой задаче можно было a раз прибавлять к текущему времени по одной минуте, аккуратно обрабатывая переполнения часов и минут.
А можно было просто посчитать ответ формулой: 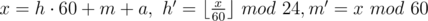 .
.
Сложность: O(a) or O(1).
Задача является значительно упрощённой версией задачи предложенной Mohammad Nematollahi Deemo.
Эту задачу можно было решать по разному, например, с помощью структур данных или sqrt-декомпозиции. Но это, конечно, делать не требовалось. Мы предполагали следующее простое линейное решение. Сделаем сначала предподсчет: для каждого числа номер первого не равного ему слева. Теперь, чтобы ответить на запрос нужно сначала проверить число в правой границе на равентсво числу x, если они не равны то мы уже нашли ответ. Если же они равны проверим первое число слева не равное числу в правой границе.
Сложность: O(n).
Задача предложена Aleksa Plavsic allllekssssa.
Давайте построим ответ в котором сумма будет равна 0. Пусть n чётно. Давайте расставим нечётные числа в первой половине массива: число 1 в позициях 1 и n, число 3 позициях 2 и n - 1 и так далее. Аналогично давайте расставим чётные числа во второй половине массива: число 2 в позициях n + 1 и 2n - 1, число 4 в позициях n + 2 и 2n - 2 и так далее. Число n мы можем поставить в оставшихся в конце свободных позициях. По аналогии ответ строится для нечётного n.
Легко видеть, что при данном построении искомая сумма равна 0.
Сложность: O(n).
Задача предложена Aleksa Plavsic allllekssssa.
Легко видеть, что ответ равен максимуму из ответов по сыновьям корня плюс один. Теперь давайте решать задачу отдельно для каждого сына v корня. Пусть z — массив глубин всех листьев в поддереве вершины v. Отсортируем z. Утверждение 1: листья выгодно поднимать в вершину v в порядке сортировки в массиве z. Утверждение 2: обозначим ax — время попадания x-го листа в вершину v и рассмотрим листья zi и zi + 1, тогда azi + 1 ≥ azi + 1. Утверждение 3: azi + 1 = max(dzi + 1, azi + 1), где dx — глубина листа x в поддереве вершины v. Последнее утверждение даём нам решение задачи: нужно просто итерироваться по массиву z слева направо и пересчитывать массив a согласно формуле из утверждения 3. Все три утверждения легко доказать и это предлагается сделать самостоятельно, чтобы лучше понять как решение работает.
Сложность: O(nlogn).
Задача предложена Иваном Поповичем NVAL.
Утверждение: функция суммы является многочленом k + 1-й степени относительно переменной n. Это утверждение можно доказать по-разному, например, можно доказать методом математической индукции (для перехода нужно взять производную от текущего многочлена).
Обозначим Px значение искомой суммы при n = x. Вычислим значения Px для всех целых значений от 0 до k + 1 (это легко сделать одним циклом за O(klogk)). Если n < k + 2, то мы уже нашли ответ. В противном случае давайте воспользуемся интерполяционным многочленом Лагранжа для получения искомого многочлена относительно переменной n.
Формула интерполяционного многочлена Лагранжа имеет вид: 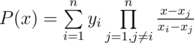 . В нашем случае xi = i - 1, а yi = Pxi.
. В нашем случае xi = i - 1, а yi = Pxi.
На этом разбор задачи был бы окончен, но это решение работает за квадратичное время от k, поскольку многочлен Лагранжа вычисляется за квадратичное время. Заметим, что у нас все узлы при интерполяции находятся на одинаковом расстоянии друг от друга (на расстоянии 1). Воспользуемся этим: заметим, что произведение внутри суммы для i + 1 может быть получено из произведения для i (нужно домножить текущее произведение на два числа и поделить на два числа). Таким образом, искомая сумма может быть посчитана за линейное время от k.
Сложность: O(klog MOD), логарифм повляется в связи с необходимостью поиска обратного элемента в поле по модулю MOD = 109 + 7.
Привет, Codeforces!
10 февраля 2016 года в 18:00 MSK состоится седьмой учебный раунд Educational Codeforces Round 7 для участников из первого и второго дивизионов.
<В прошлый раз эти абзацы всё-таки изменились>
О формате и деталях проведения учебных раундов я писал уже ранее. Также об учебных раундах вы можете прочитать здесь.
Раунд будет нерейтинговым. Соревнование будет проводиться по немного расширенным правилам ACM ICPC. На решение задач у вас будет два часа. После окончания раунда будет период времени длительностью в один день, в течение которых вы можете попробовать взломать абсолютно любое решение (в том числе свое). Причем исходный код будет предоставлен не только для чтения, но и для копирования. Таким образом вы можете локально тестировать решение, которое хотите взломать, или, например, запустить стресс-тест.
Если у вас есть идеи каких-то задач, которые вам кажутся интересными, или может есть уже что-то почти готовое, что вы по каким-то причинам не можете дать на раунд (злой координатор сказал, что задача БАЯН), официальное соревнование (жюри не хочет переграбливать соревнование), можете писать мне.
</В прошлый раз эти абзацы всё-таки изменились>
Большое спасибо Aleksa Plavsic allllekssssa, который предложил задачи D и E, и Ивану Поповичу NVAL, предложившему задачу F. Также благодарю Mohammad Nematollahi Deemo он предложил задачу, которую мы сильно упростили и решили дать в качестве задачи C.
Подготовкой задач как всегда занимался я (Эдвард Давтян). Благодарю MikeMirzayanov мы вместе придумывали задачи A, B и C. Спасибо Маше Беловой Delinur за проверку английских текстов условий. Также большое спасибо Aleksa Plavsic allllekssssa и Ивану Поповичу NVAL за тестирование задач.
На этом раунде вам по традиции будет предложено шесть задач. Мы постарались сделать задачи не очень сложными, но при этом интересными. На мой взгляд задачи чуть более математизированы, чем обычно. Надеюсь комплект задач вам понравится и вы хорошо их порешаете!
Good luck and have fun!
UPD1: Первая фаза соревнования закончена. Можете взламывать решения других участников.
UPD2: Разбор задач готов.
UPD3: Раунд закончен. Результаты окончательные.

Легко видеть, что ответ в задаче равен max(|x1 - x2|, |y1 - y2|).
Сложность: O(1).
В этой задаче достаточно было пройти по всем числам от a до b и прибавить к ответу количество сегментов, необходимое для отображения очередного числа. Для подсчёта этой величины нужно пройти по всем десятичным цифрам числа и прибавить к ответу количество сегментов, необходимой для отображения очередной цифры. Последние величины можно просто посчитать по картинке и вбить в один массив.
Сложность: O((b - a)logb).
Будем решать задачу жадно. Давайте набирать жемчужинки в самый левый хороший подотрезок по одному, начиная с первой жемчужинки. Как только подотрезок станет хорошим (то есть встретится повторение) начнём набирать новый хороший подотрезок. Если мы не смогли набрать ни одного хорошего подотрезка, то ответ - 1. В противном случае, в конце массива может остаться некоторое количество различных элементов, их нужно отнести к последнему набранному отрезку. Легко доказать, что такая жадность правильная: нужно рассмотреть первые два отрезка в оптимальном ответе и понять, что второй отрезок можно расширить пока первый не станет размера первого подотрезка в нашем ответе.
Сложность: O(nlogn).
Случаи когда нужно сделать одну операцию или их не нужно делать вовсе легко разобрать в лоб (за O(nm)). Теперь рассмотрим случай когда нужно сделать две операции. Заметим, что можно считать, что после двух операций два элемента первого массива перейдёт во второй массив и наоборот, поскольку в противном случае то же самое можно сделать и за одну операцию и значит мы уже рассмотрели этот случай. Давайте переберём пару чисел, которая перейдёт во второй массив и сложим суммы в некоторую структуру данных (например, можно сложить в map в C++). Далее переберём пару чисел во втором массиве bi, bj и найдём в нашей структуре данных сумму v наиболее близкую к числу x = sa - sb + 2·(bi + bj) и обновим ответ значением |x - v|. Нужную сумму можно искать бинарным поиском по структуре данных (для map есть функция lower_bound).
Сложность: O((n2 + m2)log(n + m)).
Запустим dfs из корня дерева и выпишем вершины в порядке в котором их обойдёт dfs (эта перестановка называется обходом Эйлера). Легко видеть, что поддерево в этой перестановке является подотрезком. Заметим, что цветов всего 60, таким образом, мы можем хранить множество цветов просто как маску двоичных битов в 64-битном типе (*long long* в C++, long в Java). Построим дерево отрезков над Эйлеровым обходом, который поддерживает операцию покраски подотрезка и нахождения маски цветов на подотрезке.
Сложность: O(nlogn).
В этой задаче неудачно были подобраны ограничения в связи с чем некоторые участники сдали решения со сложностью O(n2 + m).
Заметим сначала, что 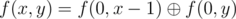 . Значения f(0, x) можно было просто предподсчитать или заметить что в зависимости от остатка числа x по модулю 4 значение функции равно x, 1, x + 1, 0 соответственно.
. Значения f(0, x) можно было просто предподсчитать или заметить что в зависимости от остатка числа x по модулю 4 значение функции равно x, 1, x + 1, 0 соответственно.
Воспользуемся алгоритмом Мо. Разобьём все запросы на  блоков по левому концу. Внутри каждого блока отсортируем запросы по правому концу. Пусть r наибольшая левая граница внутри блока, тогда все левые границы отстоят от r на расстояние не более чем
блоков по левому концу. Внутри каждого блока отсортируем запросы по правому концу. Пусть r наибольшая левая граница внутри блока, тогда все левые границы отстоят от r на расстояние не более чем  , а правые границы идут в порядке неубывания, поэтому их можно двигать по одному (в сумме на один блок мы сделаем не более n передвижений правой границы). Передвигая правую границу, внутри блока для чисел в позициях от r + 1 до текущей правой границы будем поддерживать два бора: первый для значений f(0, x - 1), второй для значений f(0, x), в первом будем поддерживать наименьшее значение x, во втором — наибольшее. Понятно как добавлять число в боры, после добавлений нужно найти наибольшее значение, которое может образовать текущий x для этого будем спускаться по первому бору, поддерживая инвариант того, что в текущем поддереве минимальное значение не больше x, и по возможности ходить по биту отличному от нашего. Аналогичное нужно делать во втором боре, только нужно поддерживать инвариант, что максимальное значение не меньше x. После того как для текущего запроса мы сдвинули правую границу на сколько нужно, нужно пройти от левой границы запроса до r и, не добавляя значения в бор, обновить ответы. Ещё отдельно для каждого запроса в новом (пустом) боре нужно пройти от левой границы до r добавляя значения в бор и обновляя ответ.
, а правые границы идут в порядке неубывания, поэтому их можно двигать по одному (в сумме на один блок мы сделаем не более n передвижений правой границы). Передвигая правую границу, внутри блока для чисел в позициях от r + 1 до текущей правой границы будем поддерживать два бора: первый для значений f(0, x - 1), второй для значений f(0, x), в первом будем поддерживать наименьшее значение x, во втором — наибольшее. Понятно как добавлять число в боры, после добавлений нужно найти наибольшее значение, которое может образовать текущий x для этого будем спускаться по первому бору, поддерживая инвариант того, что в текущем поддереве минимальное значение не больше x, и по возможности ходить по биту отличному от нашего. Аналогичное нужно делать во втором боре, только нужно поддерживать инвариант, что максимальное значение не меньше x. После того как для текущего запроса мы сдвинули правую границу на сколько нужно, нужно пройти от левой границы запроса до r и, не добавляя значения в бор, обновить ответы. Ещё отдельно для каждого запроса в новом (пустом) боре нужно пройти от левой границы до r добавляя значения в бор и обновляя ответ.
С++ solution: в коде 0-й бор соответсвует второму, а 1-й — первому.
Сложность: 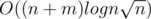 .
.
Привет, Codeforces!
21 января 2016 года в 18:00 MSK состоится шестой учебный раунд Educational Codeforces Round 6 для участников из первого и второго дивизионов.
<Здесь могла быть ваша реклама>
О формате и деталях проведения учебных раундов я писал уже ранее. Также об учебных раундах вы можете прочитать здесь.
Раунд будет нерейтинговым. Соревнование будет проводиться по немного расширенным правилам ACM ICPC. На решение задач у вас будет два часа. После окончания раунда будет период времени длительностью в один день, в течение которых вы можете попробовать взломать абсолютно любое решение (в том числе свое). Причем исходный код будет предоставлен не только для чтения, но и для копирования. Таким образом вы можете локально тестировать решение, которое хотите взломать, или, например, запустить стресс-тест.
Если у вас есть идеи каких-то задач, которые вам кажутся интересными, или может есть уже что-то почти готовое, что вы по каким-то причинам не можете дать на раунд (злой координатор сказал, что задача БАЯН), официальное соревнование (жюри не хочет переграбливать соревнование), можете писать мне.
</Здесь могла быть ваша реклама>
Большое спасибо Aleksa Plavsic allllekssssa, который предложил несколько отличных задач, две из них вы увидите на раунде (задачи D и F). Также большое пользователям Bayram Berdiyev bayram, Allanur Shiriyev Allanur, Bekmyrat Atayev Bekmyrat.A, они совместно (через Aleksa Plavsic) предложили несколько задач. Две из них вы увидите на раунде (задачи B и E).
Подготовкой задач как всегда занимался я (Эдвард Давтян). Благодарю MikeMirzayanov мы вместе придумывали задачи A и C. Спасибо Маше Беловой Delinur за проверку английских текстов условий. Также большое спасибо Aleksa Plavsic allllekssssa, который тестировал задачи и постоянно был на связи.
На этом раунде вам по традиции будет предложено шесть задач. Первая задача в этот раз проще, чем обычно (я надеюсь на очень быстрые сабмиты по ней от вас), а последняя, на мой взгляд, очень сложная (респект участникам, которые смогут её сдать). Надеюсь комплект задач вам понравится и вы хорошо их порешаете!
Good luck and have fun!
UPD 1: Забыл поблагодарить всех ребят, которые мне уже прислали идеи задач, но мы их ещё не взяли в раунд. Я постараюсь поскорее их дать.
UPD 2: Основная часть соревнования закончилась. Фаза открытых взломов открыта.
UPD 3: Разбор задач готов.
UPD 4: Соревнование закончено, результаты окончательные.

Замечу, что в этой задаче решения, использующие стандартные типы длинной арифметики (класс BigInteger в Java, стандартные длинные числа в Pyhon) не должны проходить. Это связано с тем, что они хранят число не в десятичной системе счиления и соответственно при создании длинного числа происходит его конвертация из десятичной системы счисления, которая является тяжёлой операцией и работает обычно за O(n2), где n — длина числа.
Для решения задачи можно просто добавить лидирующих нулей к более короткому числу, а далее сравнить, получившиеся строки в лексикографическом порядке (алфавитном).
Сложность: O(n).
В этой задаче нужно было сначала найти в каждой строке минимум, а далее взять максимум, получившихся минимумов. Это соответствует стратегии Павла и Наташи.
Сложность: O(nm).
Давайте сначала пронумеруем все компоненты связности, запомним для каждой её размер, а также для каждой свободной клетки запомним номер её компоненты. Это можно сделать с помощью одного обхода в глубину. Теперь ответ для непроходимой клетки будет равен единице плюс размеры всех соседних различных компонент. Соседних в смысле компонент всех соседних клеток (в общем случае четырёх).
Сложность: O(nm).
Эту задачу мы решили дать поскольку на страницах Codeforces часто видим вопрос "Что такое метод двух указателей?". Эта задача является типичным примером задачи, решаемой этим методом.
Будем искать для каждой левой границы l наибольшую границу r такую, что отрезок (l, r) k-хороший. Заметим следующее: если некоторый отрезок (l, r) k-хороший, то отрезок (l + 1, r), тоже является хорошим. Таким образом, поиск максимальной правой границы для левого конца l + 1 мы можем начинать с максимальной правой границы для левого конца l. Далее просто будем поддерживать в массиве cntx для каждого числа x количество его вхождений в текущий отрезок (l, r), а также количество различных чисел. Будем пытаться двигать правую границу пока можем, далее двигать на единицу левую границу. Итого два указателя l, r вместе передвинутся 2n раз.
Сложность: O(n).
К сожалению в этой задаче в моём решении происходило переполнение. Ошибка была исправлена во время соревнования, надеюсь это не сильно убавило вам удовольствие от решения этой задачи, поскольку она мне кажется очень интересной и красивой (идея решения, конечно, является известной для искушённых пользователей).
Сначала преобразуем сумму, которую нужно посчитать 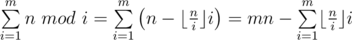 . Также заметим, что последнюю сумму можно суммировать до min(n, m), поскольку при i > n все слагаемые будут равны 0.
. Также заметим, что последнюю сумму можно суммировать до min(n, m), поскольку при i > n все слагаемые будут равны 0.
Заметим, что в последней сумме либо 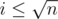 , либо
, либо 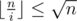 . Будем аккуратно суммировать эти два случая так, чтобы ничего не посчитать два раза. Первую сумму посчитать легко, просто нужно пройти циклом по всем таким i. Вторую сумму будем считать отдельно для всех различных значений
. Будем аккуратно суммировать эти два случая так, чтобы ничего не посчитать два раза. Первую сумму посчитать легко, просто нужно пройти циклом по всем таким i. Вторую сумму будем считать отдельно для всех различных значений 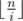 . Для этого во-первых нужно определить при каких i значение
. Для этого во-первых нужно определить при каких i значение 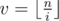 будет достигаться. Легко видеть, что это полуинтервал
будет достигаться. Легко видеть, что это полуинтервал 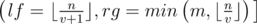 . Также нужно понять, что сумма вторых сомножителей в
. Также нужно понять, что сумма вторых сомножителей в  при постоянном первом сомножителе легко считается за константное время — это просто сумма арифметической прогрессии
при постоянном первом сомножителе легко считается за константное время — это просто сумма арифметической прогрессии 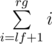 . Таким образом решение работает за
. Таким образом решение работает за  .
.
Сложность:  .
.
Эта задача была предложена и подготовлена Григорием Резниковым vintage_Vlad_Makeev. Его решение использовало суффиксный массив.
Вообще задача является типичным примером задачи на суффиксную структуру. Четверо из пяти участников сдавших задачу в основное время соревнования использовали суффиксный автомат, один использовал суффиксное дерево. Моё решение использовало суффиксное дерево, поэтому я расскажу решение с деревом (оно мне кажется простым, не считая построения самого дерева).
Построим новую строку, расположив друг за другом все строки из набора, разделив их различными разделителями. Количество разделителей порядка O(n), поэтому алфавит в суффиксном дереве тоже порядка O(n). Соответственно нужно использовать map<int, int> для хранения дерева и в асимптотике выходит O(logn). Построим для получившейся строки суффиксное дерево. Поставим в соответствие каждому разделителю строку слева от него. Теперь запустим на этом дереве обход в глубину, который никогда не переходит через разделитель и возвращает сумму цен строк, соответствующих множеству разделителей в поддереве вершины обхода в глубину. Легко видеть, что ответ это просто произведение глубины текущей вершины на сумму в поддереве этой вершины.
Сложность: O(nlogn).
Привет, Codeforces!
Поздравляю вас с наступившим новым годом! Позади остались праздники и 2015-й год, а впереди 2016-й. Желаю вам достижения всех поставленных целей и конечно удачных выступлений на соревнованиях по программированию.

11 января 2015 года в 18:00 MSK состоится пятый учебный раунд Educational Codeforces Round 5 для участников из первого и второго дивизионов.
<Год прошёл два абзаца остались>
О формате и деталях проведения учебных раундов я писал уже ранее. Также об учебных раундах вы можете прочитать здесь.
Раунд будет нерейтинговым. Соревнование будет проводиться по немного расширенным правилам ACM ICPC. На решение задач у вас будет два часа. После окончания раунда будет период времени длительностью в один день в течении, которых вы можете попробовать взломать абсолютно любое решение (в том числе свое). Причем исходный код будет предоставлен не только для чтения, но и для копирования. Таким образом вы можете локально тестировать решение, которое хотите взломать, или, например, запустить стресс-тест.
</Год прошёл два абзаца остались>
Большое спасибо Григорию Резникову vintage_Vlad_Makeev, который предложил и подготовил хорошую задачу (она будет под буквой F). Если у вас есть идеи каких-то задач, которые вам кажутся интересными, или может есть уже что-то почти готовое, что вы по каким-то причинам не можете дать на раунд (злой координатор сказал, что задача БАЯН), официальное соревнование (жюри не хочет переграбливать соревнование), можете писать мне.
Подготовкой задач как всегда занимался я (Эдвард Давтян). Благодарю MikeMirzayanov мы вместе придумывали задачи (в этот раз по телефону). Также заранее благодарю Машу Белову Delinur, которая скоро вычитает английские тексты условий.
На этом раунде вам по традиции будет предложено шесть задач. На мой взгляд в этот раз задачи проще, чем в прошлый. Исключением можно считать лишь последнюю задачу. Надеюсь комплект вам понравится и вы хорошо порешаете задачи!
Good luck and have fun!
UPD 1: Первая фаза соревнования закончена. Открыта фаза взломов.
UPD 2: Разбор задач на русском языке готов.
UPD 3: На этапе открытых взломов был обнаружен следующий спецэффект: решения на языках Python2 и Python3 имеют значительную разницу во времени выполнения в разных максимальных тестах. Например, решение на Python3 работает очень медленно на тесте из всех нулей, а на Python2 на тесте из всех девяток. Некоторые решения работают чуть больше или чуть меньше секунды, поэтому было принято решение поднять ограничение по времени в задаче А до двух секунд. Вскоре закончится фаза открытых взломов и все решения будут перетестированы.
UPD 4: Соревнование завершено. Вскоре все решения будут перетестированы на полном наборе тестов, включающем в себя взломы.
Переберём количество строк длины p и q в ответе. Пусть это величины a и b. Если a·p + b·q = n, то посторим ответ, откусив с префикса сначала a раз строки длины p, а затем b раз строки длины q. Если ни одной подходящей пары a, b не нашлось, то ответа не существует. Конечно эту задачу можно решать и за линейное время, но здесь это не требовалось, поскольку ограничение на длину строки было маленьким.
Асимптотическая сложность решения: O(n2).
612B - HDD - устаревшая технология
В условии задачи задана перестановка f. Построим по ней другую перестановку p следующим образом: pfi = i. Таким образом, перестановка p определяет номер сектора по номеру фрагмента. Перестановка p называется обратной к перестановке f и обозначается f - 1. Теперь ответ на задачу равен просто  .
.
Асимптотическая сложность решения: O(n).
612C - Заменить до правильной скобочной последовательности
Заметим, что поскольку мы не можем менять тип скобок, то для существования ответа необходимо, чтобы заданная строка была правильной скобочной последовательностью без учета вида скобок. Если это не так, то ответа не существует. Иначе каждой открывающей скобке соответствует ровно одна закрывающая, и каждой закрывающей — ровно одна открывающаяя. Теперь заметим, что если пара соответствующих друг другу скобок одного вида, то их мы можем не менять. Если же они разного вида, то поменяем вид закрывающей на вид открывающей. Таким образом, мы построим ответ. Легко убедиться, что ответ оптимальный, поскольку задачи для несоответствующих друг другу скобок не связаны друг с другом и могут быть рассмотрены по отдельности.
Единственная техническая тонкость в том как найти соответствующие друг другу скобки. Для этого заведем стек открытых скобок. Теперь будем идти по строке слева направо и если скобка открывающая, то просто добавим ее в стек. Если же она закрывающая, то возникает три случая: 1) стек пуст; 2) вверху стека лежит открывающая скобка того же вида, что и текущая закрывающая; 3) вверху стека скобка вида отличного от текущего. В первом случае ответа не существует, во втором нужно просто выкинуть открывающую скобку из стека, а в третьем нужно выкинуть открывающую скобку из стека и увеличить ответ на единицу.
Асимптотическая сложность решения: O(n).
612D - Объединение k-подотрезков
Для каждого отрезка создадим два события в момент li — открытие отрезка и в момент ri — закрытие отрезка. Отсортируем все события по моменту времени, при равенстве сначала будем обрабатывать события открытия отрезков. Это можно сделать, например, накидав в vector<pair<int, int>> events (пример для языка C++) пары момент времени и тип события ( - 1 для открытия и + 1 для закрытия). Далее это массив можно отсортировать стандартным компаратором.
Теперь будем идти по массиву events и считать баланс отрезков balance, для этого каждый раз нужно просто из баланса вычесть тип события. Теперь если баланс оказался равен k, а до этого был k - 1 значит мы стоим в левом конце отрезка из ответа, запомним этот левый конец (равный моменту текущего события) в переменную left и будем идти дальше. Если баланс оказался равен k - 1, а до этого был равен k значит мы обнаружили конец некоторого отрезка из ответа right. Добавим в ответ отрезок [left, right]. Таким образом, мы получим непересекающийся набор отрезков, содержащий все покрытые точки, в порядке слева направо. Очевидно он и является ответом на задачу.
Асимптотическая сложность решения: O(nlogn).
612E - Корень квадратный из перестановки
Рассмотрим некоторую перестанову q. Построим по ней ориентированный граф дугами, которого будут (i, qi). Этот граф, как известно, представляет собой набор неперескающихся циклов. Теперь посмотрим, что происходит с этим графом при возведениии перестановки в квадрат: все циклы нечетной длины остаются таковыми (только порядок вершин меняется, происходит чередование через одну вершину), а циклы четной длины разбиваются на два цикла вдвое меньшей длины. Таким образом, чтобы найти корень из перестановки нужно оставить все циклы нечетный длины, прочередовав их в обратном от возведения в квадрат порядке, а циклы четной одинаковой длины нужно разбить на пары и слить в один цикл (если оказывается невозможным разбиение на пары, то ответа не существует).
Асимптотическая сложность решения: O(n).
Авторское решение по этой задаче основано на динамическом программировании. На мой взгляд никакие жадные идеи в этой задаче не работают. Для решения задачи будем считать две динамики z1i — ответ на задачу если все числа меньшие ai уже выведены, а больше либо равные еще нет; и z2i — ответ на задачу если все числа меньше либо равные ai уже выведены, а большие еще нет. Введем обозначение dij — кратчайшее расстояние от i до j на кольце и odij — расстояние от i до j если идти по часовой стрелке. Легко видеть, что z2i = minj(zj + dij), по всем j таким, что aj есть наименьшее число большее ai. Пусть теперь хотим посчитать значение z1i. Рассмотрим все элементы равные ai (в одном из них мы сейчас находимся). Если такой элементв один, то z1i = z2i. Иначе у нас есть два варианта обхода этих элементов: по или против часовой стрелки. Пусть мы идём по часовой стрелке, тогда последним мы выпишем число из ближайшего к i равный элемент против часов стрелке, пусть это элемент u. Иначе последним мы последним посетим ближайший к i элемент по часовой стрелке, пусть это элемент v. Тогда z1i = min(z2u + odiu, z2v + odvi). Теперь легко видеть, что ответ на задачу равен mini(z1i + dsi), по всем i таким, что ai есть наименьший элемент в массиве, а s есть стартовая позиция. Плюс к этому ко всему как усложнение в задаче нужно было восстановить ответ. В этих случаях, на мой взгляд, проще всего написать рекурсивную реализацию динамики (хорошо протестировать её на работоспособность), затем скопировать всю динамику на восстановление ответа (для деталей выкладываю свой код). Конечно это можно делать и без копипасты, например, передавая в динамику булеву величину нужно ли восстанавливать ответ.
Асимптотическая сложность решения: O(n2).
| Название |
|---|


