665A - Автобусы между городами
Задачу предложил Сергей Эрлих unprost.
Рассмотрим интервал времени, когда Симион будет находиться на трассе строго между городами (x1, y1), (x1 = 60h + m, y1 = x1 + ta). Переберём встречный автобус. Пусть (x2, y2) — это интервал времени, когда встречный автобус будет находиться строго между городами. Если пересечение этих интервалов (x = max(x1, x2), y = min(y1, y2)) не пусто, то Симион посчитает этот автобус.
Сложность: O(1).
665B - Покупки
Задачу предложил Ayush Anand JeanValjean01.
В этой задаче нужно было сделать ровно то, что написано в условии. Никаких хитростей и подвохов.
Сложность: O(nmk).
665C - Простые строки
Задачу предложил Zi Song Yeoh zscoder.
Для решения этой задачи есть два подхода: жадность и динамическое программирование.
Первый подход: Рассмотрим некоторый отрезок из подряд идущих одинаковых букв. Пусть длина отрезка k. Очевидно мы должны изменить хотя бы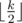 
букв в ней, чтобы не было одинаковых букв подряд. С другой стороны мы можем изменить второй, четвёртый и т.д. символы на букву, которая не равна букве слева и справа от нашего отрезка.
Второй подход: Пусть zka — наименьшее количество изменений, чтобы на префиксе длины k не было двух подряд идущих одинаковых букв и при этом символ s'k был равен букве a. Переберём букву, которую поставим на k + 1-й позиции и если она не равна a сделаем переход. Цена перехода равна 0, если мы поставили ту же букву, что стояла в исходной строке s на k + 1-й позиции. В противном случае цена равна 1.
Сложность: O(n).
665D - Красивое подмножество
Задачу предложил Zi Song Yeoh zscoder.
Рассмотрим подмножество A, являющееся ответом на задачу. Пусть a, b, c — три произвольных элемента из A и пусть не более чем один из них равен 1. По принципу Дирихле среди этих трёх чисел обязательно найдется пара чисел с одинаковой чётностью. Поскольку в этой паре только одно может быть равно 1, то их сумма чётна и больше 2. Значит подмножество A не является простым. Таким образом, A состоит либо из двух чисел больших единицы (с простой суммой), либо из некоторого количества единиц и возможно одной не единицы (если она равна простому минус один). Первый случай легко обработать за O(n2). Второй случай легко обрабатывается за линейное время. Среди двух ответов, конечно, нужно просто выбрать лучший.
Проверять на простоту числа порядка 2·106 за O(1) можно с помощью обычного или линейного решета Эратосфена.
Сложность: O(n2 + X), где X — максимальное среди заданных чисел.
665E - Красивые подмассивы
Задачу предложил Zi Song Yeoh zscoder.
Знак 
в разборе обозначает бинарную операцию побитового исключающего или.
Пусть si — xor первых i чисел на префиксе. Тогда полуинтервал (i, j] красивый если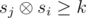 
. Будем перебирать j от 1 до n. Будем рассматривать значения sj как битовые строки. На каждой итерации к ответу нам нужно прибавить величину zj — количество чисел si (i < j) таких, что 
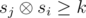. Для этого воспользуемся структурой данных бор. Будем хранить в боре все si для i < j. Кроме самой структуры бора будем в каждой вершине хранить количество листьев в поддереве этой вершины (это легко делать при добавлении новой строки). Для вычисления значения zj будем спускаться по бору, начиная из корня. Будем накапливать число cur равное префиксу ксора числа sj с путём по которому мы спустились по бору. Пусть текущий бит в sj равен b, а i — это глубина вершины в боре в которой мы находимся. Если число cur + 2i ≥ k, то мы сразу можем прибавить к zj количество листьев вершины 
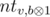, поскольку все эти листья соответствуют si-м гарантированно дающим 
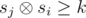. После этого мы должны спуститься в поддерево b. Если же cur + 2i < k, то мы должны просто спуститься в поддерево 
, пересчитав значение cur = cur + 2i.
Сложность по времени и памяти: O(nlogX), где X — наибольший из ксоров на префиксах.
665F - Четыре делителя
Разбор этой задачи является небольшой модификацией материалов лекции, прочитанной Михаилом Тихомировым Endagorion осенью 2015-го года в МФТИ. Большое спасибо Endagorion-у за предоставленные материалы.
Легко видеть, что только числа вида p·q и p3 (для различных простых p, q) имеют ровно четыре положительных делителя.
Посчитать количество чисел вида p3 можно просто за время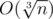 
, где n — это число из условия задачи.
Пусть теперь p < q и π(k) — это количество простых от 1 до k. Переберём значение p. Легко видеть, что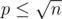 
. Таким образом, для фиксированного p мы должны увеличить ответ на значение 
.
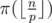Таким образом задача свелась к подсчёту значений 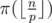— количество простых, не превосходящих величины 
для всех p.
Введём обозначение pj — j-е простое число. Пусть dpn, j — это количество k таких, что 1 ≤ k ≤ n и все простые делители k не меньше pj (заметим, что число 1 будет учтено во всех dpn, j, поскольку оно не имеет простых делителей). dpn, j удовлетворяет реккурентному соотношению:
dpn, 1 = n (поскольку $p_1$=2).
dpn, j = dpn, j + 1 + dp⌊ n / pj⌋, j, следовательно dpn, j + 1 = dpn, j - dp⌊ n / pj⌋, j.
Пусть pk — это наименьшее простое большее 
. Тогда π(n) = dpn, k + k - 1 (по определению первое слагаемое учитывает все простые не меньшие k).
Если вычислять реккурентность dpn, k напрямую, то все достижимые состояния будут иметь вид dp⌊ n / i⌋, j. Также можно заметить, что если pj и pk оба больше , то dpn, j + j = dpn, k + k. Поэтому, для всех ⌊ n / i⌋ нам достаточно хранить только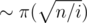 
значений dp⌊ n / i⌋, j.
Вместо прямого подсчёта всех состояний динамики, будем осуществлять двухшаноговый процесс:
Выберем K.
Запустим рекурсивное вычисление dpn, k. Если при этом в какой-то момент мы захотим посчитать значение для состояние n < K, запомним запрос ``посчитать количество чисел не больше n с простыми делителями не меньше k''.
Посчитаем ответы на все запросы в off-line: вычислим решето для чисел до K, отсортируем все числа по наименьшему простому делителю. Теперь мы можем ответить на все запросы, используя структуру данных на прибавление в точке и взятие суммы на отрезке (например, дерево Фенвика). Запомним все ответы глобально.
Снова запустим рекурсивное вычисление dpn, j. Но в этот раз если мы захотим посчитать значение для состояния n < K, мы можем использовать уже вычисленное значение.
Эффективность этой идеи сильно зависит от величины Q — количество запросов, которые нам придётся обработать.
Утверждение.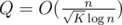 
.
Доказательство:
Каждое состояние для предпосчёта получено из dp⌊ n / pj⌋, j переходом из большего состояния. Из этого следует, что величина Q не превосходит общего количества состояний для n > K.
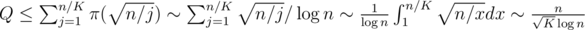
Предпосчёт ответов для Q запросов может быть выполнен за время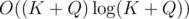 
и это наиболее ёмкая часть вычислений. Выбирая оптимальным образом значение 
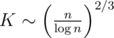, мы получаем сложность всего решения 
.
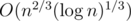Сложность: .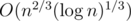
