691A - Берляндская мода
Задачу предложил и подготовил Артур Яворски KingArthur.
В задаче нужно было просто сделать то, что написано в условии.
Сложность: O(n).
691B - s-палиндром
Задачу предложил Никита Мельников nickmeller.
В задаче нужно было аккуратно по картинке определить симметричные буквы, а также заметить, что пары букв (b, d) и (p, q) являются зеркальными отражениями.
Сложность: O(n).
691C - Экспоненциальная запись
Задачу предложил пользователь blowUpTheStonySilence.
Эта реализационная задача. Нужно было сделать ровно то, что написано в условии задачи. На мой взгляд, проще всего было найти позицию первой ненулевой цифры и позицию точки. Разность этих двух позиций равна числу b (если значение положительно нужно вычесть единичку).
Сложность: O(n).
691D - Свопы в перестановке
Задачу предложил Zi Song Yeoh zscoder.
Рассмотрим граф из n вершин, рёбрами которого являются заданные пары позиций. В каждой компоненте связности этого графа мы можем поменять значения в любых двух позициях. Соответственно мы можем все значения отсортировать в порядке убывания. Легко видеть, что полученная перестановка является лексикографически максимальной.
Сложность: O(n + m).
691E - Xor-последовательности
Задачу предложил Zi Song Yeoh zscoder.
Пусть zij — количество xor-последовательностей длины i с последним элементом aj. Пусть gij равно 1 если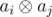 
содержит количество единиц в бинарном представлении кратное трём, и равно 0 в противном случае. Расмотрим векторы чисел zi = {zij}, zi - 1 = {zi - 1, j} и матрицу G = {gij}. Легко видеть, что zi = G × zi - 1. Соответственно, zn = Gn × z0. В силу ассоциативности операции матричного умножения можно сначала вычислать Gn бинарным возведением в степень матрицы и затем умножить полученную матрицу на z0.
Сложность: O(n3logk).
691F - Couple Cover
Задачу предложил Michael Kirsche mkirsche.
Будем считать количество пар с произведением меньшим p. Получить количество не меньших, можно вычитая из общего количества пар n·(n - 1) количество меньших. Пусть cnti количество чисел в a раных i, а zj — количество пар из a с произведением равным j. Для подсчета массива z можно воспользоваться по сути решетом Эратосфена: переберём первое число a, а также кратное ему b = ka и увеличим zb на величину cnta·cntk. После предподсчёта массива z достаточно предподсчитать массив его частичных сумм, чтобы отвечать на запросы о количество пар меньших p.
Сложность: O(n + XlogX), где X — наибольшее значение в массиве p.
