Let's denote the potion's amount of experience as exp and its cost as cost. We want to know if there is a potion such that exp and cost meet the following condition: 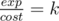 . To do this, we can iterate on cost from x to y and check that exp = k·cost is not less than l and not greater than r.
. To do this, we can iterate on cost from x to y and check that exp = k·cost is not less than l and not greater than r.
To understand whether some piece of sausage intersects with pizza, we can check if their borders intersect. And to check this, since their borders are circles, we are interested in their radii and the distance between their centers.
To check if a piece of sausage is inside the crust, we firstly check that it is inside the pizza 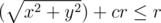 ), and secondly check that it is completely outside the central part of the pizza
), and secondly check that it is completely outside the central part of the pizza 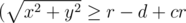 ).
).
It's easy to see that if the number written on some vertex i is not equal to 0, then its beauty will be some divisor of ai. Also if the number written on the root is 0 then the beauty of each vertex can be easily calculated. Otherwise beauty of each vertex will be a divisor of the number in the root.
Let's calculate the beauty of each vertex if the number in the root is 0. This can be done by traversing the tree, and the beauty of i is gcd(ai, ans[pari]).
If the number in the root is not 0, then possible values of beauty for each vertex are among divisors of this number. For each of these divisors we can maintain how many numbers on the path from the root to current vertex are divisible by that divisor. When we enter or leave some vertex, we need to update this information by iterating on divisors of the number in the root. If we maintain it and current depth d, then we can calculate the possible beauty of current vertex. It is equal to greatest divisor such that there are at least d - 1 numbers on the path that are divisible by this divisor.
842D - Vitya and Strange Lesson)
If the last query was xi and then we receive a query xi + 1, then we can leave the original array unchanged and use the number 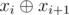 as the second query. So we will maintain current xor of queries instead of changing the array.
as the second query. So we will maintain current xor of queries instead of changing the array.
It's easy to see that if the array contains all numbers from zero to 2k - 1 and the number in the query is less than 2k, then the array will still contain all those numbers.
Let's store all numbers from the array in binary trie and maintain the number of leaves in each subtree.
To answer each query, we will descend the trie. We need to get the lowest possible answer, so if current bit of the number in the query equals i (i = 0 or i = 1), so we firstly check the subtree that corresponds to bit i. We will descend into the vertex only if the subtree is not a complete binary tree (so there exists a number that would belong to this subtree but is not included in the array). When we try to descend into an empty subtree, then we set all remaining bits in the answer to zero.
The vertices in the answer are the endpoints of some diameter of the tree.
Let's consider diameter (a, b), where a and b are its endpoints, and we add a new vertex с. Then the length of diameter either remains the same or increases by one (then new endpoints are vertices (a, c) or (b, c)).
We have to maintain current centers of the tree (there are not more than two centers). If the length of diameter increases, then the number of centers changes (but there will always exist a vertex that was the center before the query and remains the center after the query).
Let's build a segment tree on the eulerian tour of the tree. The vertex that maintains the segment [l, r] will store current maximal distance to the center and the number of vertices that have this distance. Then the answer for the query will be stored in the root of the segment tree.
When we add a new vertex, we need to check whether the length of diameter increases; this can be done with LCA. If the diameter increases, we update centers and distances to them.










