Like for 75 we have (5,5,3), (25,3),(15,5),(75,1). Similarly how to do this for any given number if that number is given in its prime-factorised form?
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | adamant | 151 |
| 7 | djm03178 | 151 |
| 7 | luogu_official | 151 |
| 10 | awoo | 146 |
Each edge — 'i' in the graph has two values associated with it — v1[i] and v2[i].
Let M be one of the possible Spanning Tree of the graph. Then define A = max(v1[i]'s for all the edges in ST) and B = max(v2[i]'s for all the edges in the ST).
Then for all the possible Spanning Trees of this graph find the minimum value of A + B.
Problem Link -> https://www.hackerearth.com/practice/algorithms/graphs/biconnected-components/tutorial/
Go to the bottom of the page for the problem.
Is the visible test case for the problem correct?
#include<bits/stdc++.h>
using namespace std;
#define endl "\n"
#define MOD 1000000007
#define setprec(ans) cout<<fixed<<std::setprecision(9)<<ans<<endl;
typedef vector<int> VI;
typedef vector<VI> VVI;
typedef long long int ll;
ll find_combinations(VI &cycles){
ll ans=0;
for(auto x: cycles){
ans = (ans + ((ll)x*(x-1)))%MOD;
}
return ans;
}
void dfs_1(int x, int &c, VVI &graph, VI &in, VI &out, VI &parent){
in[x] = ++c;
for(auto child: graph[x]){
if(in[child] == INT_MAX){
//this vertex is not visited yet
parent[child] = x;
dfs_1(child, c, graph, in, out, parent);
if(out[child] <= in[x]){
out[x] = min(out[x], out[child]);
}
}
else{
//visited, can be a parent or ancestor
if(parent[x] != child){
//ancestor
out[x] = min(out[x], in[child]);
}
}
}
}
int dfs_2(int x, VVI &graph, VI &in, VI &out, VI &vis){
vis[x] = 1;
int c = 1;
for(auto child: graph[x]){
if(!vis[child] && in[child] >= out[child]) c += dfs_2(child, graph, in, out, vis);
}
return c;
}
void solve(){
int n, m;cin>>n>>m;
VVI graph(n);
for(int i=0;i<m;i++){
int u, v;cin>>u>>v;
//u--, v--;
graph[u].push_back(v);
graph[v].push_back(u);
}
VI in(n, INT_MAX), out(n, INT_MAX), parent(n, -1);
int c=0;
for(int i=0;i<n;i++){
if(in[i] == INT_MAX){
dfs_1(i, c, graph, in, out, parent);
}
}
VI cycles;
int odd_count = 0, even_count = 0;
VI vis(n, 0);
for(int i=0;i<n;i++){
if(in[i] >= out[i] && (vis[i] == 0)){
int temp = dfs_2(i, graph, in, out, vis);
if(temp%2 == 1) odd_count++;
else even_count++;
}
}
cout<<odd_count<<" "<<even_count;
//cout<<find_combinations(cycles);
}
int main()
{
ios_base:: sync_with_stdio(false); cin.tie(0);
int t;t=1;
//cin>>t;
while(t--){
solve();
}
return 0;
}
We have three containers whose capacities are m litres, n litres, and p litres respectively (assume m > n > p). The n-litre and p-litre containers start out full of water, but the m-litre container is initially empty. We are allowed one type of operation: pouring the contents of one container into another, stopping only when the source container is empty or the destination container is full. We want to find the smallest sequence of pourings (if it exists) that leaves exactly x litres in the n-litre or p-litre container where (x ≤ p). If there are multiple smallest sequences, output any one of them.
How to model this question as a graph problem?
"I tried to write down all the possible states of m, n, p and then taking these states as the nodes. But didn't get any manage-able graph which has finite no of states."
In an array — 'arr' there are n elements. Two elements arr[i] and arr[j] can be combined to one element if arr[i] >= k * arr[j], for i != j. After combination, these two elements cannot further combine with any other element of the array. Find the minimum size of the array possible, after executing atmost n/2 operations.
Input will be n, the array elements and k.
Problem Link ---> https://codeforces.net/contest/364/problem/E
I've read the editorial, but I'm unable to understand the algo. Can anyone give a better explanation, or some resources to understand this problem. I need to understand this problem, before applying a similar logic to another problem. A similar problem appeared in one of my divid-and-conquer based test, a while ago.
You are playing a game on a machine. First of all the machine chooses a number N. You do not know this number and you need to make guesses to find it. Suppose you choose the number k, the machine tells whether k is less than, equal to or greater than N. The game ends if k is equal to N. If you guess a number which is greater than N, then it is considered a bad guess. You cannot make more than 1 bad guess.
Expected time complexity is sqrt(n) time. I find it impossible to do, when only one bad guess is allowed. Any help would be appreciated.
I'm solving a problem in which I need to store the frequency of each digit from 0 to 9 in a bitmask.
Is it possible to do this?
If yes, then how?
Given two arrays S[] and E[] of size N denoting starting and closing time of the shops and an integer value K denoting the number of people, the task is to find out the maximum number of shops they can visit in total if they visit each shop optimally based on the following conditions:
A shop can be visited by only one person A person cannot visit another shop if its timing collide with it Examples:
Input: S[] = {1, 8, 3, 2, 6}, E[] = {5, 10, 6, 5, 9}, K = 2 Output: 4 Explanation: One possible solution can be that first person visits the 1st and 5th shops meanwhile second person will visit 4th and 2nd shops.
Input: S[] = {1, 2, 3}, E[] = {3, 4, 5}, K = 2 Output: 3 Explanation: One possible solution can be that first person visits the 1st and 3rd shops meanwhile second person will visit 2nd shop.
My solution approach code -->
bool mycomp(const pair<int, int> &p1, const pair<int, int> &p2){
if(p1.second == p2.second){
return p1.first > p2.first;
}
return p1.second < p2.second;
}
int maximumActivities_1_person(vector<pair<int, int>> &v, int &totalRemaining, VI &visited){
int ans=0, n=v.size(), last_end = -1;
for(int i=0;i<n;i++){
if((last_end == -1 || (last_end != -1 && v[i].first >= last_end)) && visited[i] == 0) ans++, last_end = v[i].second, totalRemaining--, visited[i]=1;
}
return ans;
}
int maximumActivities_K_persons(VI &start, VI &end, int K){
int n = start.size();
vector<pair<int, int>> v;
for(int i=0;i<n;i++){
v.push_back({start[i], end[i]});
}
sort(v.begin(), v.end(), mycomp);
int totalRemaining = n;
VI visited(n, 0);
int no_of_workers = K;
int ans=0;
while(totalRemaining && no_of_workers){
no_of_workers--;
int c = maximumActivities_1_person(v, totalRemaining, visited);
cout<<c<<endl;
ans+=c;
}
return ans;
}
void solve(){
int n, K;cin>>n>>K;
VI start(n, 0), end(n, 0);
for(int i=0;i<n;i++){
cin>>start[i]>>end[i];
}
cout<<maximumActivities_K_persons(start, end, K)<<endl;
}
Is my algorithm correct?
There is no online judge on which this problem is present so I cannot test against the test cases. So if anyone can validate if the algorithm devised by me is correct.
These are the approaches that i have tried but getting TLE
Use a 3d array and continue just like we do LCS of two strings.
Complexity = O(n^3).
First take the first two strings, find the length of LCS, then recover all the LCS of these two strings using backtracking on the DP array of these two strings.
Then use these recovered LCS and find the LCS length of these strings with the last string that was given to us, and take the max len of these LCS's as the answer. Complexity = O(n^2) + complexity of recovering all the LCS strings of the first two strings
This is the link to the question ---> https://www.codingninjas.com/codestudio/problems/lcs-of-3-strings_842499?topList=top-fintech-software-engineer-interview-questions&leftPanelTab=0
Can anyone suggest a more efficient method to do this question.
--- This is the code for second method. ``` VVI lcs(string a, string b){ int n1=a.length(), n2 = b.length();
VVI dp(n1+1, VI (n2+1, 0));
for(int i=1;i<=n1;i++){
for(int j=1;j<=n2;j++){
if(a[i-1] == b[j-1]){
dp[i][j] = 1 + dp[i-1][j-1];
}
dp[i][j] = max(dp[i-1][j], max(dp[i][j], dp[i][j-1]));
//cout<<dp[i][j]<<" ";
}
//cout<<endl;
}
return dp;
}
string recoverLCS(string a, string b, VVI &dp, int i, int j){ //int n1 = a.length(), n2 = b.length();
if(i == 0 || j == 0) return "";
if(a[i-1] == b[j-1]){
return a[i-1] + recoverLCS(a, b, dp, i-1, j-1);
}
if(dp[i-1][j] > dp[i][j-1]) return recoverLCS(a, b, dp, i-1, j);
return recoverLCS(a, b, dp, i, j-1);
}
vector recoverAllLCS(string a, string b, VVI &dp, int i, int j){ if(i == 0 || j == 0) return {""};
if(a[i-1] == b[j-1]){
vector<string> temp = recoverAllLCS(a, b, dp, i-1, j-1);
for(int z=0;z<(int)temp.size();z++){
temp[z] = a[i-1] + temp[z];
}
// for(auto x: temp){
// x = a[i-1] + x;
// }
return temp;
}
else if(dp[i-1][j] > dp[i][j-1]){
return recoverAllLCS(a, b, dp, i-1, j);
}
else if(dp[i-1][j] < dp[i][j-1]){
return recoverAllLCS(a, b, dp, i, j-1);
}
else{
vector<string> vs1 = recoverAllLCS(a, b, dp, i-1, j);
vector<string> vs2 = recoverAllLCS(a, b, dp, i, j-1);
for(auto x: vs1){
vs2.push_back(x);
}
return vs2;
}
} vector returnAllLCS(string a, string b){ VVI dp = lcs(a, b); int n1=a.length(), n2 = b.length();
vector<string> v = recoverAllLCS(a, b, dp, n1, n2);
unordered_set<string> ans(v.begin(), v.end());
// for(auto x: ans){
// reverse(x.begin(), x.end());
// cout<<x<<endl;
// }
vector<string> final(ans.begin(), ans.end());
return final;
} ```
This is the code for first method.
VVVI dp(n1+1, VVI (n2+1, VI (n3+1, 0)));
int ans=0;
for(int i=1;i <= n1;i++){
for(int j=1;j <= n2;j++){
for(int k=1;k <= n3;k++){
if(a[i] == b[j] && b[j] == c[k]){
dp[i][j][k] = 1 + dp[i-1][j-1][k-1];
}
vector<int> di = {0, 0, -1};
vector<int> dj = {0, -1, 0};
vector<int> dk = {-1, 0, 0};
for(int z=0;z<(int)di.size();z++){
dp[i][j][k] = max(dp[i][j][k], dp[i+di[z]][j+dj[z]][k+dk[z]]);
}
ans=max(ans, dp[i][j][k]);
}
}
}
`
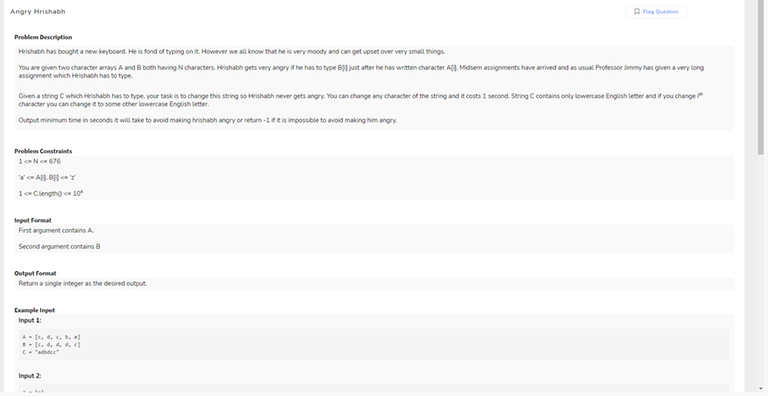 How to solve this? I once solved a problem in which one change depended on other, but unable to recall the method.
How to solve this? I once solved a problem in which one change depended on other, but unable to recall the method.
https://i.imgur.com/EQ8NLOa.png
Here is the link to the original image.
| Name |
|---|










