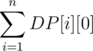Hello,
Recently my friend encountered the following problem during a coding interview:
You are given a string $$$S$$$ and a set $$$T$$$ of $$$n$$$ strings. You need to choose a multiset from $$$T$$$ (you can choose the same string any number of times) and then concatenate the strings from the multiset in any order to obtain the string $$$S$$$. What is the maximum possible size of such a multiset?
There is a simple $$$O(|S|^2)$$$ solution using DP + trie. First add all strings from $$$T$$$ to a trie. Let $$$DP[i]$$$ be the answer for $$$S_{i...|S|-1}$$$. To calculate $$$DP[i]$$$, we traverse the trie according to the substring $$$S_{i...|S|-1}$$$, and try to update $$$DP[i]$$$ for each string we encounter in the trie.
Assuming the sum of the lengths of strings from the set $$$T$$$ is $$$X$$$, there is also a solution with complexity $$$O(|S| * sqrt(X))$$$:
Is there a faster solution to this problem? I've tried for a long time without any success.
Any help would be appreciated, thanks!









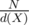 to ans.
to ans.
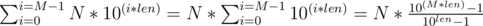
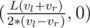 let it be
let it be 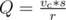 where
where 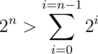 , we should try to match each bit with it's opposite greedily starting with the most significant bit.
, we should try to match each bit with it's opposite greedily starting with the most significant bit. 

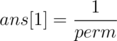
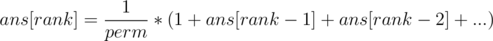
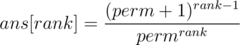
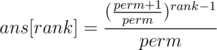

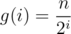
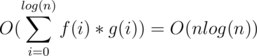
 and store them in an array
and store them in an array