I've just turned International Grandmaster. Now you can ask me anything in the comments.
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | djm03178 | 152 |
| 7 | adamant | 152 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
Author: TheScrasse
Preparation: TheScrasse
Suppose you want to choose pieces of cake $$$i$$$, $$$j$$$. Can you make them adjacent in $$$1$$$ move?
The answer is the sum of the $$$2$$$ maximum weights.
You can always pick the $$$2$$$ maximum weights: if they are $$$a_i$$$ and $$$a_j$$$ ($$$i < j$$$), you can flip the subsegment $$$[i, j-1]$$$ to make them adjacent.
The result can't be larger, because the sum of the weights of any $$$2$$$ pieces of cake is never greater than the sum of the $$$2$$$ maximum weights.
Iterating over all pairs of pieces of cake is enough to get AC, but you can solve the problem in $$$O(n \log n)$$$ by sorting the weights and printing the sum of the last $$$2$$$ values, or even in $$$O(n)$$$ if you calculate the maximum and the second maximum in linear time.
Complexity: $$$O(t \cdot n^2)$$$, $$$O(t \cdot n \log n)$$$ or $$$O(t \cdot n)$$$
Official solution: 150288088
Author: emorgan
Preparation: TheScrasse
Are there any characters that you can never remove?
You can't remove the rightmost occurrence of each letter. Can you remove the other characters?
If you can remove $$$s_1, s_2, \dots, s_{i-1}$$$ and $$$s_i$$$ is not the rightmost occurrence of a letter, you can also remove $$$s_i$$$.
Let $$$a$$$ be the initial string. For a string $$$z$$$, let's define $$$z(l, r) = z_lz_{l+1} \dots z_r$$$, i.e., the substring of $$$z$$$ from $$$l$$$ to $$$r$$$. The final string is $$$a(k, n)$$$ for some $$$k$$$.
In the final string, $$$x = 0$$$, so the first character doesn't appear anywhere else in $$$s$$$. This means that $$$a_k\not=a_{k+1}, a_{k+2}, \dots, a_n$$$. In other words, $$$a_k$$$ is the rightmost occurrence of a letter in $$$s$$$.
Can you ever remove $$$a_i$$$, if $$$a_i\not=a_{i+1}, a_{i+2}, \dots, a_n$$$? Notice that you would need to remove $$$a(l, r)$$$ ($$$l \leq i \leq r$$$): this means that there must exist $$$a(l', r') = a(l, r)$$$ for some $$$l' > l$$$. So, $$$a_{i+l'-l} = a_i$$$, and this is a contradiction.
Therefore, $$$k$$$ is the smallest index such that $$$a_k\not=a_{k+1}, a_{k+2}, \dots, a_n$$$.
You can find $$$k$$$ by iterating over the string from right to left and updating the frequency of each letter. Indeed $$$a_i\not=a_{i+1}, a_{i+2}, \dots, a_n$$$ if and only if the frequency of the letter $$$a_i$$$ is $$$0$$$ up to now (in the iteration from right to left we are performing). The value of $$$k$$$ is the minimum such index $$$i$$$.
Complexity: $$$O(n)$$$
Official solution: 150288210
Author: emorgan
Preparation: TheScrasse
Can you find the initial weight which results in $$$a$$$?
The initial weight is the sum of the final weights. Let's simulate the division, starting from a new cake. How to choose fast which splits to do?
If the largest piece is not in $$$a$$$, you have to split it. How to find the largest piece efficiently?
Keep $$$a$$$ and the new cake in two multisets or priority queues.
First, let's find the initial weight. When a piece of cake is split, the sum of weights is $$$\lfloor\frac{w}{2}\rfloor + \lceil\frac{w}{2}\rceil$$$:
- if $$$w$$$ is even, $$$\lfloor\frac{w}{2}\rfloor + \lceil\frac{w}{2}\rceil = \frac{w}{2} + \frac{w}{2} = w$$$;
- if $$$w$$$ is odd, $$$\lfloor\frac{w}{2}\rfloor + \lceil\frac{w}{2}\rceil = \frac{w-1}{2} + \frac{w+1}{2} = w$$$.
Therefore, the sum of weights is constant, and the initial weight is the sum of the final weights.
Now let's start from a cake $$$b$$$ of weight $$$b_1 = \sum_{i=1}^n a_i$$$, split it (into pieces of weight $$$b_i$$$) and try to make it equal to $$$a$$$. At any moment, it's convenient to consider the largest $$$b_i$$$, because you can determine if you can split it or not.
More specifically,
- if $$$b_i$$$ is not in $$$a$$$, you have to split it;
- if $$$b_i = a_j$$$ for some $$$j$$$, you can only match $$$a_j$$$ with $$$b_i$$$ or with a $$$b_k$$$ such that $$$b_k = a_j = b_i$$$ (because there doesn't exist any larger $$$b_k$$$): that's equivalent to removing $$$a_j$$$ and $$$b_i$$$ from $$$a$$$, $$$b$$$, respectively.
Notice that, if at any moment the maximum element of $$$b$$$ is smaller than the maximum element of $$$a$$$, the answer is NO.
If can keep $$$a$$$ and $$$b$$$ in any data structure that supports inserting an integer, asking for the maximum and removing the maximum (e.g., multiset or priority queue), the following algorithm works.
While either $$$a$$$ or $$$b$$$ is not empty,
- if the maximum element of $$$b$$$ is smaller than the maximum element of $$$a$$$, print
NOand break; - if the maximum element of $$$b$$$ is equal to the maximum element of $$$a$$$, remove it from both $$$a$$$ and $$$b$$$;
- if the maximum element $$$m$$$ of $$$b$$$ is larger than the maximum element of $$$a$$$, remove it from $$$b$$$ and split the piece of cake (i.e., insert $$$\lfloor\frac{w}{2}\rfloor$$$ and $$$\lceil\frac{w}{2}\rceil$$$ into $$$b$$$).
If $$$a$$$ or $$$b$$$ are both empty at the end, the answer is YES.
Complexity: $$$O(n \log n)$$$
Official solution: 150288232
Author: emorgan
Preparation: TheScrasse
The $$$n-1$$$ facts make a tree.
Assume that the amount of ingredient $$$1$$$ is $$$1$$$. For each $$$i$$$, the amount of ingredient $$$i$$$ would be $$$c_i/d_i$$$ for some integer $$$c_i, d_i > 0$$$. How to make an integer amount of each ingredient?
The optimal amount of ingredient $$$1$$$ is $$$\text{lcm}(d_1, d_2, \dots, d_n)$$$.
Can you find the exponent of each prime $$$p \leq n$$$ in $$$\text{lcm}(d_1, d_2, \dots, d_n)$$$?
If you visit the nodes in DFS order, each edge changes the exponent of $$$O(\log n)$$$ primes. At each moment, keep the factorization of $$$c_i/d_i$$$ of the current node, i.e., the exponents of each $$$p \leq n$$$ (they can be negative). For each $$$p$$$, also keep the minimum exponent so far.
Read the hints. The rest is just implementation.
Start a DFS from node $$$1$$$. Keep an array $$$f$$$ such that $$$f_p$$$ is the exponent of $$$p$$$ in the amount of ingredients of the current node. Keep also $$$v_i = c_i/d_i \,\, \text{mod} \,\, 998\,244\,353$$$. At the beginning, the amount of ingredients (of node $$$1$$$) is $$$1$$$, so $$$f_p = 0$$$ for each $$$p$$$. Whenever you move from node $$$i$$$ to node $$$j$$$, and $$$r_i/r_j = x/y$$$,
- for each $$$p^k$$$ such that $$$p^k \mid x$$$ and $$$p^{k+1} \nmid x$$$, decrease $$$f_p$$$ by $$$k$$$;
- for each $$$p^k$$$ such that $$$p^k \mid y$$$ and $$$p^{k+1} \nmid y$$$, increase $$$f_p$$$ by $$$k$$$.
Notice that there exist $$$O(\log n)$$$ such values of $$$p^k$$$ for each edge, and you can find them by precalculating either the smallest prime factor (with the sieve of Eratosthenes) or the whole factorization of every integer in $$$[2, n]$$$.
Let $$$g_p$$$ be the minimum value of $$$f_p$$$ during the DFS. Then, for every $$$p$$$, you have to multiply the amount of ingredients of node $$$1$$$ by $$$p^{-g_p}$$$.
The answer is the sum of $$$v_i$$$, multiplied by the amount of ingredients of node $$$1$$$.
Complexity: $$$O(n \log n)$$$
Official solution: 150288255
1654E - Арифметические операции
Author: emorgan
Preparation: TheScrasse
Consider each element of the array as being a point in the plane $$$(i, a_i)$$$. Then all of the elements that don't get affected by an operation lie on a single line in the plane. Find a line that maximizes the number of points on it.
Let $$$m$$$ be the upper bound on $$$a_i$$$. The intended complexity is $$$O(n \sqrt m)$$$.
Let $$$m$$$ be the upper bound on $$$a_i$$$. Let $$$d$$$ be the difference between adjacent elements in the final array. Create a piecewise algorithm for the cases where $$$|d| < \sqrt m$$$ and $$$|d| \geq \sqrt m$$$
As explained in the hints, instead of computing the fewest number of operations, we will compute the largest number of elements that don't have an operation on them, and we will create a piecewise algorithm with final complexity $$$O(n\sqrt m)$$$ , where $$$m$$$ is the upper bound on $$$a_i$$$.
Let $$$d$$$ be the common difference between elements in our final sequence. First of all, I will assume that $$$d \geq 0$$$, since solving the problem for negative $$$d$$$ is as simple as reversing the array and running the solution again. If $$$d$$$ is fixed beforehand, we can solve the problem in $$$O(n)$$$ by putting element $$$i$$$ into bucket $$$a_i-d\cdot i$$$ and returning $$$n$$$ minus the size of the biggest bucket.
For $$$d < \sqrt m$$$, we can use the above algorithm to handle all of these $$$d$$$ in $$$O(n \sqrt m)$$$ time. We can keep a hashmap from bucket index $$$\to$$$ number of elements in the bucket, or we can just keep an array since the bucket indices have a range of at most $$$O(n \sqrt m)$$$ which is not enough to exceed the memory limit.
For $$$d \geq \sqrt m$$$, we observe that if we have two indices $$$i, j$$$ such that $$$j > i+\sqrt m$$$, then at least one of them definitely has to have an operation performed on it, because the difference between them would have to be $$$a_j-a_i \geq \sqrt m \cdot d > m$$$ which is not possible. In other words, if we consider the set of elements which are not edited, that set will have gaps between pairs of elements of size at most $$$\sqrt m$$$.
So, we can build a graph between indices with an edge $$$i \to j$$$ with label $$$x$$$ if $$$i < j \leq i+\sqrt m$$$ and $$$\frac{a_j-a_i}{j-i} = x$$$. This graph has at most $$$n\sqrt m$$$ edges. Then we just have to find the longest path in the graph where all edges have the same label. You can do this with dynamic programming -- let $$$dp_{i,d}$$$ be the length of the longest path ending at index $$$i$$$, where all edges have label $$$d$$$. For each $$$i$$$, we only need to check edges to $$$j$$$ where $$$i - \sqrt m < j < i$$$. This means the time complexity is $$$O(n\sqrt m)$$$. To store the values $$$dp_{i,d}$$$ sparsely, we can use either a hash map or a rotating buffer (where we only store $$$dp_{i,d}$$$ for $$$i$$$ in a sliding window of width $$$\sqrt m$$$).
Complexity: $$$O(n \sqrt m)$$$
Official solution: 150288285
1654F - Минимальное XOR-ирование строки
Author: dario2994, emorgan
Preparation: dario2994, TheScrasse
Let $$$f(s, x)$$$ be the string $$$t$$$ such that $$$t_i = s_{i\oplus x}$$$. The intended solution not only finds the $$$x$$$ such that $$$f(s, x)$$$ is lexicographically minimized, but produces an array of all $$$0 \leq x < 2^n$$$ sorted according the comparator $$$f(s, i) < f(s, j)$$$.
The solution is similar to the standard method to construct a suffix array.
Let $$$a_k$$$ be an array of the integers $$$0$$$ through $$$2^n-1$$$, sorted according to the lexicographic ordering of the first $$$2^k$$$ characters of $$$f(s, x)$$$. The answer to the problem is $$$f(s, a_{n,0})$$$. Given the array $$$a_{k-1}$$$, can you compute $$$a_k$$$?
Let $$$f(s, x)$$$ be the string $$$t$$$ such that $$$t_i = s_{i\oplus x}$$$.
The solution is inspired by the standard method to construct a suffix array. Let $$$a_k$$$ be an array containing the integers $$$0, 1, 2,\dots, 2^n-1$$$, sorted according to the lexicographic ordering of the prefixes of length $$$2^k$$$ of the strings $$$f(s, 0), f(s, 1), \dots, f(s, 2^n-1)$$$ (i.e., the prefix of length $$$2^k$$$ of $$$f(s, a_k[i])$$$ is lexicographically smaller or equal than the prefix of length $$$2^k$$$ of $$$f(s, a_k[i+1])$$$). We can construct $$$a_k$$$ using $$$a_{k-1}$$$, and $$$a_0$$$ is easy to construct as a base case.
In order to construct $$$a_k$$$ from $$$a_{k-1}$$$, we will first construct an auxiliary array of integers $$$v$$$ using $$$a_{k-1}$$$, where $$$v_i < v_j$$$ iff $$$f(s, i)_{0..2^{k-1}} < f(s, j)_{0..2^{k-1}}$$$. Then, we will sort the array $$$a_k$$$ according to the comparison of tuples $$$(v_i, v_{i\oplus {2^{k-1}}}) < (v_j, v_{j\oplus {2^{k-1}}})$$$.
Once we have $$$a_n$$$, then we just print $$$f(s, a_{n,0})$$$. In total, the solution takes $$$O(2^n n^2)$$$ time, which can be optimized to $$$O(2^n n)$$$ using the fact that tuples of integers in the range $$$[0, m]$$$ can be sorted using radix sort in $$$O(m)$$$ time. This optimization was not required to get AC.
Official solution: 150288326
Author: emorgan
Preparation: dario2994, emorgan, TheScrasse
Let's say that a vertex is "flippable" if it has at least one neighbor of the same height. The optimal strategy for a skier is to ski to a flippable vertex with lowest height, flip back and forth between that vertex and its neighbor until all energy is used, and then ski to a base lodge.
Assuming the skier starts at vertex $$$v$$$ and chooses vertex $$$u$$$ as the flippable vertex to flip back and forth at, this skier will "waste" a total of $$$h_u$$$ units of kinetic energy for a total path length of $$$2h_v-h_u$$$. Note that if no such $$$u$$$ exists, then the maximum amount of $$$h_v$$$ will be wasted as the skier goes straight to a base lodge. Let $$$w_v$$$ be this "wasted" amount. Instead of computing the maximum path length for the skier starting at vertex $$$v$$$, compute $$$w_v$$$. The answer for that vertex is $$$2h_v-w_v$$$.
Try to solve this seemingly unrelated problem: Let $$$S$$$ be the set of flippable vertices. What is the largest possible value of $$$\sum\limits_{v\in S}h_v$$$?
The largest possible value of $$$\sum\limits_{v\in S}h_v$$$ is $$$O(n)$$$. Therefore, there are at most $$$O(\sqrt n)$$$ distinct values of $$$w_v$$$ across all vertices. Solve for each value of $$$w_v$$$ separately.
Read the hints. The rest is just implementation.
For each set of flippable vertices of the same height, we can calculate the set of starting vertices which are able to reach at least one vertex in that flippable set. To do this, split the graph up into layers of equal height. Let $$$c_v$$$ be the minimum required energy to reach a vertex in the flippable set. $$$c_v$$$ can be computed via shortests paths, where edges in the same layer have weight $$$1$$$ and edges from layer $$$i$$$ to $$$i+1$$$ have weight $$$-1$$$. We can use bfs to relax the costs of vertices in a single layer, and then easily transition to the next layer. We do this for $$$O(\sqrt n)$$$ different starting heights, so the total complexity is $$$O(n\sqrt n)$$$.
Official solution: 150288345
Author: dario2994, TheScrasse
Preparation: dario2994, TheScrasse
If $$$p_1,\dots, p_n$$$ is good and $$$p_i=1$$$, what can you say about $$$p_1,p_2,\dots, p_i$$$ and $$$p_i,p_{i+1},\dots, p_n$$$?
Find a quadratic solution ignoring the constraints given by the string $$$s$$$.
Find an $$$O(n^2 + nm)$$$ solution taking care of the constraints given by the string $$$s$$$.
Optimize the $$$O(n^2+nm)$$$ solution using generating functions.
The solution to the ODE $$$y'(t) = a(t)y(t) + b(t)$$$ with $$$y(0)=1$$$ is given by $$$\exp(\smallint a)\Big(1+\int b\exp(-\smallint a)\Big)$$$
First of all, let us state the following lemma (which is sufficient to solve the problem in $$$O(n^2)$$$ if one ignores the constraints given by the string $$$s$$$). We omit the proof as it is rather easy compared to the difficulty of the problem as a whole.
Lemma: The following statements hold for a permutation $$$p_1,p_2,\dots, p_n$$$.
- $$$p$$$ is good if and only if $$$p[1:i]$$$ and $$$p[i:n]$$$ are good, where $$$p_i = 1$$$.
- If $$$p_1=1$$$, then $$$p$$$ is good if and only if $$$p[1:i]$$$ and $$$p[i:n]$$$ are good, where $$$p_i = 2$$$.
- If $$$p_1=1$$$ and $$$p_n=2$$$, then $$$p$$$ is good if and only if it is bitonic, i.e., $$$p_1<p_2<p_3<\cdots<p_i>p_{i+1}>\cdots p_{n-1}>p_n$$$, where $$$p_i=n$$$.
Given $$$1\le l < r\le n$$$, we say that a permutation $$$q_1,q_2,\dots, q_{r-l+1}$$$ of $$${1,2,\dots, r-l+1}$$$ is $$$[l,r]$$$-consistent if for any $$$l\le i \le \min(r, m-1)$$$:
- $$$q_{i-l+1} < q_{i-l+2}$$$ if $$$s_i = \texttt{<}$$$;
- $$$q_{i-l+1} > q_{i-l+2}$$$ if $$$s_i = \texttt{>}$$$.
Informally speaking, a permutation is $$$[l,r]$$$-consistent if it satisfies the constraints given by $$$s$$$ when it is written in the positions $$$[l, r]$$$.
For $$$1\le l<r\le n$$$, let $$$a_{\ast\ast}(l, r)$$$, $$$a_{1\ast}(l, r)$$$, $$$a_{\ast 1}(l, r)$$$, $$$a_{12}(l, r)$$$, $$$a_{21}(l, r)$$$ be the the number of good permutations which are $$$[l,r]$$$-consistent and, respectively,
- No additional conditions;
- Start with $$$1$$$;
- End with $$$1$$$;
- Start with $$$1$$$ and end with $$$2$$$;
- Start with $$$2$$$ and end with $$$1$$$.
For $$$1\le i < n$$$ and $$$c\in{\texttt{<}, \texttt{>}}$$$, let $$$q(i, c) := [i>m\text{ or } s_i= c]$$$. Informally speaking, $$$q(i, \texttt{<})$$$ is $$$1$$$ if and only if it can be $$$p_i<p_{i+1}$$$ and $$$q(i, \texttt{>})$$$ is $$$1$$$ if and only if it can be $$$p_i > p_{i+1}$$$.
Thanks to the Lemma, one has the following relations:
- $$$a_{\ast\ast}(l, r) = \sum_{i=l}^r a_{\ast1}(l, i) a_{1\ast}(i, r) \binom{r-l}{i-l}$$$.
- $$$a_{1\ast}(l, l) = 1$$$. For $$$l < r$$$, $$$a_{1\ast}(l, r) = \sum_{i=l+1}^r a_{12}(l, i)a_{1\ast}(i, r)\binom{r-l-1}{i-l-1}$$$.
- Analogous formula for $$$a_{\ast 1}$$$.
- $$$a_{12}(l, l) = 0$$$ and $$$a_{12}(l, l+1)= q(l, \texttt{<})$$$ and $$$a_{12}(l, l+2)= q(l, \texttt{<})\cdot q(l+1, \texttt{>})$$$. For $$$l<l+1<r$$$, $$$a_{12}(l, r) = q(l, \texttt{<})a_{21}(l+1, r) + q(r-1, \texttt{>})a_{12}(l, r-1)$$$.
- Analogous formula for $$$a_{21}$$$.
The problem asks to compute $$$a_{\ast\ast}(1, n)$$$. Thanks to the formulas stated above, it is straightforward to implement an $$$O(n^2)$$$ solution. Now we will tackle the hard task of optimizing it to $$$O(nm + n\log(n))$$$.
In order to compute $$$a_{\ast\ast}(1, n)$$$, we will compute $$$a_{\ast1}(1, k)$$$ and $$$a_{1\ast}(k, n)$$$ for all $$$1\le k\le n$$$.
We have the recurrence relation (for $$$k\ge 2$$$)
Setting $$$x_{k-1} := a_{\ast1}(1, k) / (k-1)!$$$, (1) is equivalent to (for $$$k\ge 1$$$, and also for $$$k=0$$$!)
This looks very similar to an identify between generating functions (a derivative on the left, a product on the right); but for the fact that $$$a_{21}$$$ depends on two parameters. To overcome this issue let us proceed as follows.
Notice that, if we set $$$b$$$ to any of the functions $$$a_{\ast\ast}$$$, $$$a_{\ast1}$$$, $$$a_{1\ast}$$$, $$$a_{12}$$$, $$$a_{21}$$$, it holds $$$b(l, r) = b(l+1, r+1)$$$ whenever $$$l > m$$$. Hence, let us define $$$b_{\ast\ast}(k) = a_{\ast\ast}(n+1, n+k)$$$ and analogously $$$b_{1\ast}(k)$$$, $$$b_{\ast 1}(k)$$$, $$$b_{12}(k)$$$, $$$b_{21}(k)$$$.
With these new definitions, (2) becomes (for $$$k\ge 0$$$)
Let $$$u_i:= \frac{b_{21}(i+2)}{i!}$$$ and $$$v_{k-1}:= \sum_{i=0}^{\min(k-1, m-1)} x_i \frac{b_{21}(k+1-i) - a_{21}(i+1, k+1)}{(k-1-i)!}$$$. So, (3) simplifies to
We precompute in $$$O(nm)$$$ the values of $$$a_{12}(l, r)$$$ and $$$a_{21}(l, r)$$$ for $$$1\le l\le m$$$, $$$l < r\le n$$$. We can also precompute in $$$O(n)$$$ the values of $$$b_{12}(k), b_{21}(k)$$$ for $$$1\le k\le n$$$. In $$$O(m^2)$$$ we compute also $$$x_i$$$ for all $$$0\le i\le m-1$$$. Thus, in $$$O(nm)$$$ we can compute, for all $$$0\le k < n$$$, the values $$$u_k$$$.
It is now time to start working with generating functions. Let $$$X(t):= \sum_{k\ge 0} x_k t^k$$$, $$$U(t):=\sum_{k\ge0} u_kt^k$$$, $$$V(t):=\sum_{k\ge0} v_kt^k$$$. We know $$$U(t)$$$ and $$$V(t)$$$ (at least the first $$$n$$$ coefficients) and we want to compute $$$X(t)$$$. Since $$$x_0=1$$$, we know $$$X(0)=1$$$. Moreover (4) is equivalent to the ordinary differential equation $$$X' = V + U\cdot X$$$. This ODE is standard and its (unique) solution is given by
Since the product of generating functions and the exponential of a generating function can be computed in $$$O(n\log(n))$$$, we are able to obtain the values of $$$x_k$$$ for all $$$0\le k <n$$$ and thus the values of $$$a_{\ast 1}(1,k)$$$.
Now, let us see how to compute $$$a_{1\ast}(k, n)$$$. Since $$$a_{1\ast}(k,n) = b_{1\ast}(n-k+1)$$$ for all $$$m<k\le n$$$, let us first compute $$$b_{1\ast}(k)$$$ for all $$$1\le k\le n$$$. By repeating verbatim the reasoning above, we get that the generating function $$$Y(t):=\sum_{k\ge 0} y_k t^k$$$, where $$$y_{k-1}:=b_{1\ast}(k) / (k-1)!$$$, is given by ($$$V=0$$$ in this case) $$$Y=\exp(\int U)$$$. So, it remains only to compute $$$a_{1\ast}(k, n)$$$ for $$$1\le k\le m$$$. This can be done naïvely in $$$O(nm)$$$.
The overall complexity is $$$O(nm + n\log(n))$$$.
Official solution: 150306974
Hello everyone,
in this tutorial we will see a trick that can be useful in combinatorics and/or DP tasks. In particular, you can use it when the statement says something similar to "the score of an array is the product of its elements, find the sum of the scores over all the possible arrays".
Prerequisites: basic combinatorics and DP
The trick
The trick is very simple.
"The score of an array $$$a$$$ is $$$\prod_{i=1}^n a_i$$$" can be rephrased as "if there are $$$n$$$ boxes, and the $$$i$$$-th box contains $$$a_i$$$ distinguishable balls, the score of $$$a$$$ is equal to the number of ways to color a ball for each box".
This is quite obvious, but it can be extremely powerful. Let's see some problems that are trivialized by this trick.
Dwango Programming Contest 6th, problem C (rating: 2618)
You have to output the sum of the happiness over all possible combinations of choices.
Use the trick. At the end of the process, for each child color one of his cookies in red. You have to output the number of combination of choices, if you assume that the coloring is a choice too. What if you distribute red cookies during the $$$k$$$ days instead of coloring cookies at the end?
Now the problem becomes "In the $$$i$$$-th day, we will choose $$$a_i$$$ children and give either a red cookie or a normal cookie to each child chosen. In how many ways each children ends up having exactly one red cookie?"
Let's find a DP. You can simulate rounds. Which information do you need after each round?
After each round, you only need the number of children who have already received a red cookie.
If you use the trick, the problem becomes "In the $$$i$$$-th day, we will choose $$$a_i$$$ children and give either a red cookie or a normal cookie to each child chosen. In how many ways each children ends up having exactly one red cookie?".
You can calculate the answer with DP. Let $$$dp_{i, j}$$$ be the number of ways to distribute the candies in the first $$$i$$$ rounds and give a red cookie to exactly $$$j$$$ children. When you calculate $$$dp_{i, j}$$$, you can iterate over the number $$$m$$$ of red cookies distributed in the last round. The transition is $$$dp_{i, j} = \sum_{m=0}^{\min(j, a_i)} dp_{i-1, j-m} \cdot \binom{n-j+m}{m} \cdot \binom{n-m}{a_i-m}$$$. In fact, there are
- $$$dp_{i-1, j-m}$$$ ways to distribute candies in the previous rounds
- $$$\binom{n-j+m}{m}$$$ ways to choose the children who receive a red cookie
- $$$\binom{n-m}{a_i-m}$$$ ways to choose the children who receive a normal cookie
The answer is $$$dp_{k, n}$$$.
Complexity: $$$O(n^2k)$$$.
abc231_g (rating: 2606)
This problem is very similar to the previous one. The differences are that the boxes already contain some balls and $$$k$$$ is large (but the operation are simpler, because you insert exactly $$$1$$$ ball for each operation).
Let's deal with the first difference. In the previous problem, when did we use the fact that the boxes were initially empty?
Hint 5 in the previous problem is true because the boxes were initially empty (so they also were initially equal). In this problem, is it possible to avoid dealing with the $$$a_i$$$ during the operations (e.g. can you do some preprocessing before considering the operations)?
Let's color the balls already in the boxes. You can calculate the number of ways to color $$$m$$$ balls with DP.
Now we can iterate over the number $$$m$$$ of balls colored initially.
For each $$$m$$$, the problem becomes "In how many ways can you put $$$k$$$ balls in the boxes and color $$$n-m$$$ of them, one for each box without already colored balls?"
Instead of coloring the balls at the end, you can choose the operations where you put a red ball in a box. In how many ways can you do that?
Use the trick. First, fix the number of colored balls that were already in the boxes before the operations. Let $$$dp_{i, j}$$$ be the number of ways to color exactly $$$j$$$ balls in the first $$$i$$$ boxes. The transition is $$$dp_{i, j} = dp_{i-1, j} + a_i \cdot dp_{i-1, j-1}$$$.
If you color exactly $$$m$$$ boxes before the operations, the number of ways is $$$dp_{n, m}$$$, multiplied by the number of ways to put $$$k$$$ balls in the boxes and color $$$n-m$$$ of them, one for each box without already colored balls.
Now let's deal with the $$$k$$$ operations. Let's fix which operations add a red ball ($$$\binom{k}{n-m}$$$ ways), the order of red balls ($$$(n-m)!$$$ ways) and the boxes chosen in the other operations ($$$n^{k-n+m}$$$).
Therefore, the answer is $$$\frac{1}{n^m} \cdot \sum_{m=0}^{n} dp_{n, m} \cdot \binom{k}{n-m} \cdot (n-m)! \cdot n^{k-n+m}$$$
Complexity: $$$O(n^2)$$$.
You can replace the DP with a small to large NTT, and the complexity becomes $$$O(n \log^2 n)$$$.
In the official editorial, there is a solution with polynomials and linearity of expectation. Find the similarities between this solution and the one in the editorial.
arc124_e (rating: 3031)
$$$S$$$ can be obtained by only considering sequences where at least a person hands $$$0$$$ balls to the neighbor on his right.
Use the trick. For each person $$$i$$$, his red ball was initially owned either by $$$i$$$ or by the neighbor on his left.
Use DP. In how many ways can you distribute and color the balls for each prefix? You need additional information:
- the array is circular, so you need to know if person $$$1$$$ has already a colored ball (that wasn't given by person $$$n$$$)
- while processing person $$$i$$$, you need to know if he has already received a colored ball
- you need to know if at least a person in the prefix has given $$$0$$$ balls to the neighbor on his right
Let's do an example of transition. If you want to color one of the balls of person $$$i$$$ and give some balls to his neighbor, including a colored ball, the number of ways can be calculated by fixing the number $$$m$$$ of balls given. For a fixed $$$m$$$, the answer is $$$m(a_i-m)$$$. The total number of ways is $$$\sum_{m=1}^{a_i} m(a_i-m) = a_i \cdot \sum_{m=1}^{a_i} m - \sum_{m=1}^{a_i} m^2 = \frac{a_i^2(a_i+1)}{2} - \frac{a_i(a_i+1)(2a_i+1)}{6}$$$. The other transitions are similar.
Use the trick. Let $$$dp_{i, j, k, l}$$$ the number of ways the people numbered from $$$1$$$ to $$$i$$$ can give and color balls, considering that
- the person $$$1$$$ has colored $$$j$$$ balls ($$$0 \leq j \leq 1$$$)
- the neighbor to the right of person $$$i$$$ has received $$$k$$$ colored balls ($$$0 \leq k \leq 1$$$)
- if $$$l = 0$$$, no person has given $$$0$$$ balls to his neighbor; if $$$l = 1$$$, at least one person has given $$$0$$$ balls to his neighbor.
The transitions can be found by iterating on the answers of the following questions:
- must the person $$$i$$$ color one of his balls?
- how many balls can $$$i$$$ give to his neighbor?
- must the person $$$i$$$ give a colored ball to his neighbor?
An example of transition (with formulas) is in Hint 4.
The answer is the sum of $$$dp_{n, j, 1-j, 1}$$$ (because person $$$1$$$ must have exactly $$$1$$$ colored ball, and there must be a person who has given $$$0$$$ balls to his neighbor).
Complexity: $$$O(n)$$$.
Other problems
arc147_d - Sets Scores (rating: 2145)
abc214_g - Three Permutations (rating: 2893) (suggested by __hermit__)
agc013_e - Placing Squares (rating: 3455) (zscoder)
1842G - Tenzing and Random Operations
IOI 2022/4 - Digital Circuit
abc225_h - Social Distance 2 (rating: 3061) (__hermit__)
Conclusions
We've seen that "product trick" is very useful to find a DP that solves the problem. There exist similar counting tricks: for example, "The score of an array $$$a$$$ is $$$\sum_{i=1}^n a_i^2$$$" can be rephrased as "if there are $$$n$$$ boxes, and the $$$i$$$-th box contains $$$a_i$$$ distinguishable balls, the score of $$$a$$$ is equal to the number of ordered pairs of balls belonging to the same box" (you can try to use it in 1278F - Cards).
Of course, suggestions/corrections are welcome. In particular, please share in the comments other problems where you can use this trick.
I hope you enjoyed the blog!
UPD: I was wrong :(
UPD2: I was wrong, again.
Hello everyone,
I see that many people complain about copied problems. Their claim is that authors weren't able to come up with some problems, and decided to copy them from other sources instead.
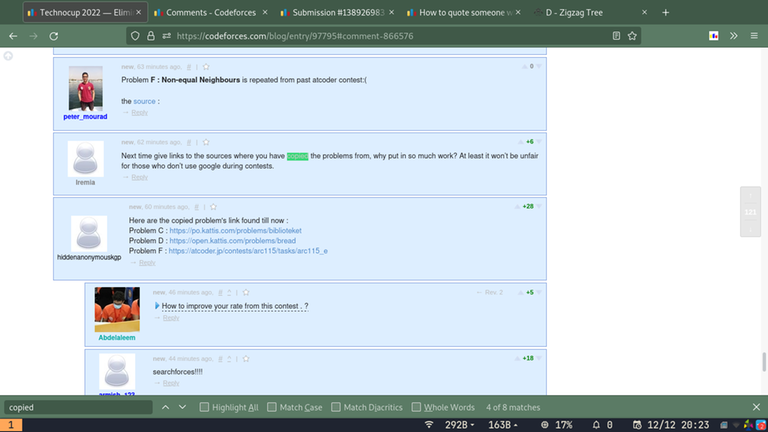
Although a contest shouldn't have already used problems, please convince yourself that no problemsetter would copy problems deliberately. The presence of some problems from the Internet is accidental. So, it's not correct to accuse the authors to "copy" the problems.
FAQ:
Q. The statement is completely the same, isn't it obvious that the problem was copied?
A. No. Proof: I invented 844C - Sorting by Subsequences and 1088D - Ehab and another another xor problem, with the same statement. Usually, if you want to write the statement formally, there is only one way that's much more convenient to use that the others.
Q. Maybe you remembered the statement because you had already read it without solving the problem?
A. No. Proof: I invented 1501C - Going Home and arc130_d before the contest.
Q. How is it possible that no author / tester was able to find the "copied" problem by googling?
A. Challenge: find arc115_e on Google, using only the statement of 1591F - Non-equal Neighbours.
Hello everyone,
this blog is similar to 90744, but it's specifically about implementation.
Although practicing for around 2 years, I'm still very slow in implementation. For example, during olympiads I usually spend ~ 70% of the time writing the code, so I don't have much time to think.
In fact,
- during CEOI 2021 Mirror (Day 2) I spent a lot of time writing ~ 220 lines of code for problem C (the logic of that solution was wrong, but that's another story)
- I've just solved CEOI 2016/1 (submission), but my solution is 239 lines long.
- I don't perform well on DMOJ (my contests: 1, 2, 3)
- I spent 1:30 hours implementing 101597A, although my final code is only 81 lines long.
How to improve? Should I learn new C++ features? Should I start implementing something significantly longer than competitive programming problems?
Hello everyone,
problems about swapping adjacent elements are quite frequent in CP, but they can be tedious. In this tutorial we will see some easy ideas and use them to solve some problems of increasing difficulty. I tried to put a lot of examples to make the understanding easier.
The first part of the tutorial is quite basic, so feel free to skip it and jump to the problems if you already know the concepts.
Target: rating $$$[1400, 2100]$$$ on CF
Prerequisites: greedy, Fenwick tree (or segment tree)
Counting inversions
Let's start from a simple problem.
You are given a permutation $$$a$$$ of length $$$n$$$. In one move, you can swap two elements in adjacent positions. What's the minimum number of moves required to sort the array?
Claim
The result $$$k$$$ is equal to the number of inversions, i.e. the pairs $$$(i, j)$$$ ($$$1 \leq i < j \leq n$$$) such that $$$a_i > a_j$$$.
Proof 1
Let $$$f(x)$$$ be the number of inversions after $$$x$$$ moves.
In one move, if you swap the values on positions $$$i, i + 1$$$, $$$f(x)$$$ either increases by $$$1$$$ or decreases by $$$1$$$. This is because the only pair $$$(a_i, a_j)$$$ whose relative order changed is $$$(a_i, a_{i+1})$$$. Since the sorted array has $$$0$$$ inversions, you need at least $$$k$$$ moves to sort the array.
For example, if you have the permutation $$$[2, 3, 7, 8, 6, 9, 1, 4, 5]$$$ ($$$16$$$ inversions) and you swap two adjacent elements such that $$$a_i > a_{i+1}$$$ (getting, for example, $$$[2, 3, 7, 6, 8, 9, 1, 4, 5]$$$), the resulting array has $$$15$$$ inversions, and if you swap two adjacent elements such that $$$a_i < a_{i+1}$$$ (getting, for example, $$$[3, 2, 7, 8, 6, 9, 1, 4, 5]$$$), the resulting array has $$$17$$$ inversions.
On the other hand, if the array is not sorted you can always find an $$$i$$$ such that $$$a_i > a_{i+1}$$$, so you can sort the array in $$$k$$$ moves.
Proof 2
For each $$$x$$$, let $$$f(x)$$$ be the number of inversions if you consider only the elements from $$$1$$$ to $$$x$$$ in the permutation.
First, let's put $$$x$$$ at the end of the permutation: this requires $$$x - \text{pos}(x)$$$ moves. That's optimal (the actual proof is similar to Proof 1; in an intuitive way, if you put the last element to the end of the array, it doesn't interfere anymore with the other swaps).
For example, if you have the permutation $$$[2, 3, 7, 8, 6, 9, 1, 4, 5]$$$ and you move the $$$9$$$ to the end, you get $$$[2, 3, 7, 8, 6, 1, 4, 5, 9]$$$ and now you need to sort $$$[2, 3, 7, 8, 6, 1, 4, 5]$$$. Hence, $$$f(x) = f(x-1) + x - \text{pos}(x)$$$. For each $$$x$$$, $$$x - \text{pos}(x)$$$ is actually the number of pairs $$$(i, j)$$$ ($$$1 \leq i < j \leq x$$$) such that $$$x = a_i > a_j$$$. So $$$f(x)$$$ is equal to the number of inversions.
Counting inversions in $$$O(n \log n)$$$
You can use a Fenwick tree (or a segment tree). There are other solutions (for example, using divide & conquer + merge sort), but they are usually harder to generalize.
For each $$$j$$$, calculate the number of $$$i < j$$$ such that $$$a_i > a_j$$$.
The Fenwick tree should contain the frequency of each value in $$$[1, n]$$$ in the prefix $$$[1, j - 1]$$$ of the array.
So, for each $$$j$$$, the queries look like
- $$$res := res + \text{range_sum}(a_j + 1, n)$$$
- add $$$1$$$ in the position $$$a_j$$$ of the Fenwick tree
Observations / slight variations of the problem
By using a Fenwick tree, you are actually calculating the number of inversions for each prefix of the array.
You can calculate the number of swaps required to sort an array (not necessarily a permutation, but for now let's assume that its elements are distinct) by compressing the values of the array. For example, the array $$$[13, 18, 34, 38, 28, 41, 5, 29, 30]$$$ becomes $$$[2, 3, 7, 8, 6, 9, 1, 4, 5]$$$.
You can also calculate the number of swaps required to get an array $$$b$$$ (for now let's assume that its elements are distinct) starting from $$$a$$$, by renaming the values. For example,
$$$a = [2, 3, 7, 8, 6, 9, 1, 4, 5], b = [9, 8, 5, 2, 1, 4, 7, 3, 6]$$$
is equivalent to
$$$a = [4, 8, 7, 2, 9, 1, 5, 6, 3], b = [1, 2, 3, 4, 5, 6, 7, 8, 9]$$$
$$$a^{-1}$$$ (a permutation such that $$$(a^{-1})_{a_x} = x$$$, i.e. $$$(a^{-1})_x$$$ is equal to the position of $$$x$$$ in $$$a$$$) has the same number of inversions as $$$a$$$. For example, $$$[2, 3, 7, 8, 6, 9, 1, 4, 5]$$$ and $$$[7, 1, 2, 8, 9, 5, 3, 4, 6]$$$ have both $$$16$$$ inversions. Sketch of a proof: note that, when you swap two elements in adjacent positions in $$$a$$$, you are swapping two adjacent values in $$$a^{-1}$$$, and the number of inversions in $$$a^{-1}$$$ also increases by $$$1$$$ or decreases by $$$1$$$ (like in Proof 1).
1430E - String Reversal (rating: 1900)
This problem seems very similar to "calculate the number of swaps required to get an array $$$b$$$ (with distinct elements) starting from $$$a$$$", but there can be equal elements.
Some swaps are useless (which ones?)
It's useless to swap equal characters. For each character, can you get its final position in the reversed string? (Treat equal characters as distinguishable values)
Note that it's useless to swap equal characters (in fact, the string doesn't change and you waste $$$1$$$ move).
Consider each character $$$c$$$ from 'a' to 'z' separately. The relative order of a subsequence of equal characters doesn't change in the optimal solution.
Hence, the $$$i$$$-th leftmost occurrence of $$$c$$$ in the initial string should move to the $$$i$$$-th leftmost occurrence of $$$c$$$ in the reversed string. If you number each character of the string, treating equal characters as distinguishable values, you can calculate the array $$$a$$$ such that $$$a_i$$$ is the final position of $$$s_i$$$ in the reversed string, and the result is the number of inversions of $$$a$$$.
For example, consider the string acabcaaababbcb. The reversed string is bcbbabaaacbaca. The positions of 'b' in the reversed string are $$${1, 3, 4, 6, 11}$$$, and this means that $$$a_4 = 1, a_9 = 3, \dots, a_{14} = 11$$$ (in fact, $$$a = [5, 2, 7, 1, 10, 8, 9, 12, 3, 14, 4, 6, 13, 11]$$$).
103148B - Luna Likes Love (EGOI 2021/2)
If there are two adjacent elements, it's optimal to remove them.
In Proof 1, we've seen that a swap changes the number of inversions by $$$1$$$. Here, you should calculate something slightly different than the number of inversions.
Consider two pairs of equal elements. What should their relative positions be at the end?
The answer is $$$n + \text{# of pairs of integers (x, y) such that their order in the array is xyxy}$$$. Can you calculate it efficiently?
Consider two pairs of equal elements (integers $$$(x, y)$$$). If you want to remove those pairs, in some moment their relative positions should be $$$\text{xyyx}$$$ (or $$$\text{yxxy}$$$). Instead, if the relative positions are $$$\text{xyxy}$$$, you want to swap two of these elements. If $$$k$$$ is the number of pairs of integers $$$(x, y)$$$ such that their order in the array is $$$\text{xyxy}$$$, do you need exactly $$$k$$$ swaps (and $$$n$$$ removals)? It turns out that the answer is yes. Sketch of a proof:
- if there are no $$$\text{xyxy}$$$, there are two adjacent equal elements (so you can remove them)
- if you remove two adjacent equal elements, the number of $$$\text{xyxy}$$$ doesn't change
- if there are no adjacent equal elements, there is a $$$\text{xyxy}$$$ such that two of these characters are adjacent (so you can swap them and eliminate a $$$\text{xyxy}$$$)
Now let's calculate $$$k$$$. Let $$$(x_i, y_i)$$$ be $$$n$$$ pairs such that $$$x_i < y_i, a_{x_i} = a_{y_i}$$$: now you have to calculate, for each $$$j$$$, how many indices $$$i$$$ meet $$$x_i < x_j, x_j < y_i < y_j$$$.
You can use a Fenwick tree that contains how many times each value in $$$[1, n]$$$ occurs as a $$$y_i$$$, considering only pairs such that $$$x_i < x_j$$$.
So, for each $$$j$$$, the queries look like
- $$$res := res + \text{range_sum}(x_j + 1, y_j - 1)$$$
- add $$$1$$$ in the position $$$y_j$$$ of the Fenwick tree
arc088_e (rating: 2231)
When is the answer -1?
The answer is -1 if there are $$$\geq 2$$$ characters with an odd number of occurrences in the string. Otherwise, can you calculate the optimal final position of each character, like in 1430E - String Reversal?
Once again, it's useless to swap equal characters. So, what's the relative position of equal characters? Which characters should be located in symmetrical positions (i.e. $$$i, n - i + 1$$$)?
The $$$i$$$-th leftmost occurrence and the $$$i$$$-th rightmost occurrence of a character $$$c$$$ in the initial string should move to symmetrical positions in the final string. Let's consider such "symmetrical pairs": what's the optimal relative order of two pairs with distinct letters? What about the letter in the center of the string (if its length is odd)?
If there are $$$\geq 2$$$ characters with an odd number of occurrences in the string, you can't make a palindrome.
Since it's useless to swap equal characters, you know which pairs of characters will stay on symmetrical positions in the final string, i.e. the $$$i$$$-th leftmost occurrence and the $$$i$$$-th rightmost occurrence of any character $$$c$$$.
In the string acabcaaababbc, for example, you can make these "symmetrical pairs": positions $$$(1, 10), (2, 13), (3, 8), (4, 12), (6, 7), (9, 11)$$$. The character in position $$$5$$$ should go in the center of the final string (i.e. position $$$7$$$).
The symmetrical pairs have to be nested inside each other, in some order. Given two symmetrical pairs, which of them should be located outside the other one?
It turns out that the pair that contains the leftmost element should be located outside. In fact, if you want to reach $$$\text{xyyx}$$$, the initial configurations with $$$x$$$ on the left ($$$\text{xxyy}$$$, $$$\text{xyxy}$$$, $$$\text{xyyx}$$$) require $$$2, 1, 0$$$ moves respectively, while reaching $$$\text{yxxy}$$$ requires $$$2, 1, 2$$$ moves respectively.
So you can sort the symmetrical pairs by leftmost element and construct the array $$$a$$$ such that $$$a_i$$$ is the final position of $$$s_i$$$ in the palindromic string (in this case, $$$[1, 2, 3, 4, 7, 5, 9, 11, 6, 13, 8, 10, 12]$$$) and the result is the number of inversions of $$$a$$$.
arc097_e (rating: 2247)
Which balls can you put at the end?
At the end, you have a ball with number $$$n$$$. For example, if it's white, you have to sort the remaining $$$n-1$$$ white balls and $$$n$$$ black balls. How to calculate efficiently the cost required?
Let $$$dp_{i,j}$$$ be the minimum cost required to sort the first $$$i$$$ white balls (with a number from $$$1$$$ to $$$i$$$) and the first $$$j$$$ black balls (with a number from $$$1$$$ to $$$j$$$). You need transitions in $$$O(1)$$$.
Re-read Proof 2 in this tutorial.
It's easy to prove that the leftmost $$$k$$$ balls in the final arrangement are the white balls with a number in $$$[1, i]$$$ and the black balls with a number in $$$[1, j]$$$ for some $$$i, j$$$ such that $$$i+j = k$$$.
For fixed $$$i, j$$$, let $$$dp_{i,j}$$$ be the minimum cost (considering only such balls). If the last ball is white, you can move it immediately to the end (see Proof 2), and the cost is the number of $$$l$$$ in the initial array such that
- $$$l \leq i - 1$$$ if the ball is white, $$$l \leq j$$$ if the ball is black
- $$$\text{pos}(l) > \text{pos}(i)$$$
Then you spend $$$dp_{i-1,j}$$$ to sort the rest of the array. You can calculate the cost similarly if the last ball is black.
Computing such transitions in $$$O(1)$$$ can be done with simple prefix sums (for example, let $$$ps_{i, c, j}$$$ be the number of balls with position $$$\geq i$$$, color $$$c$$$ and value $$$\leq j$$$).
The result is $$$dp_{n,n}$$$.
Other problems
IOI 2019/1
arc120_c (suggested by Ghassane)
Hackerearth — Swapping numbers (Inferno03)
Hackerearth — Make the strings equal (Inferno03)
1526D - Kill Anton (somil_jain_120)
JOI 2021/3 (Final Round) (you can submit here)
Conclusions
We've seen that a lot of problems where you have to swap adjacent elements can be tackled with greedy observations, such as looking at the optimal relative positions of the values in the final array; then, a lot of these problems can be reduced to "find the number of inversions" or similar.
Of course, suggestions/corrections are welcome. In particular, please share in the comments other problems where you have to swap adjacent elements.
I hope you enjoyed the blog!
Hello everyone,
here is a very simple idea that can be useful for (cp) number theory problems, especially those concerning multiples, divisors, $$$\text{GCD}$$$ and $$$\text{LCM}$$$.
Prerequisites: basic knowledge of number theory (divisibility, $$$\text{GCD}$$$ and $$$\text{LCM}$$$ properties, prime sieve).
Idea
Let's start from a simple problem.
You are given $$$n$$$ pairs of positive integers $$$(a_i, b_i)$$$. Let $$$m$$$ be the maximum $$$a_i$$$. For each $$$k$$$, let $$$f(k)$$$ be the sum of the $$$b_i$$$ such that $$$k | a_i$$$. Output all pairs $$$(k, f(k))$$$ such that $$$f(k) > 0$$$.
An obvious preprocessing is to calculate, for each $$$k$$$, the sum of the $$$b_i$$$ such that $$$a_i = k$$$ (let's denote it as $$$g(k)$$$). Then, there are at least $$$3$$$ solutions to the problem.
Solution 1: $$$O(m\log m)$$$
For each $$$k$$$, $$$f(k) = \sum_{i=1}^{\lfloor m/k \rfloor} g(ik)$$$. The complexity is $$$O\left(m\left(\frac{1}{1} + \frac{1}{2} + \dots + \frac{1}{m}\right)\right) = O(m\log m)$$$.
Solution 2: $$$O(n\sqrt m)$$$
There are at most $$$n$$$ nonzero values of $$$g(k)$$$. For each one of them, find the divisors of $$$k$$$ in $$$O(\sqrt k)$$$ and, for each divisor $$$i$$$, let $$$f(i) := f(i) + g(k)$$$.
If $$$m$$$ is large, you may need to use a map to store the values of $$$f(k)$$$ but, as there are $$$O(n\sqrt[3] m)$$$ nonzero values of $$$f(k)$$$, the updates have a complexity of $$$O(n\sqrt[3] m \log(nm)) < O(n\sqrt m)$$$.
Solution 3: $$$O(m + n\sqrt[3] m)$$$
Build a linear prime sieve in $$$[1, m]$$$. For each nonzero value of $$$g(k)$$$, find the prime factors of $$$k$$$ using the sieve, then generate the divisors using a recursive function that finds the Cartesian product of the prime factors. Then, calculate the values of $$$f(k)$$$ like in solution 2.
Depending on the values of $$$n$$$ and $$$m$$$, one of these solutions can be more efficient than the others.
Even if the provided problem seems very specific, the ideas required to solve that task can be generalized to solve a lot of other problems.
1154G - Minimum Possible LCM
$$$\text{LCM}$$$ is quite uncomfortable. Rephrase the problem using $$$\text{GCD}$$$.
Use $$$\text{LCM}(a, b) = \frac{ab}{\text{GCD}(a, b)}$$$. Now you can solve the problem separately for each $$$k = \text{GCD}(a_i, a_j)$$$ ($$$i \neq j$$$). What are the optimal values of $$$a_i, a_j$$$?
For a fixed $$$k$$$, it's optimal to choose the minimum $$$a_i, a_j$$$ that are multiples of $$$k$$$. How to find those minimums? Does it matter if, actually, $$$\text{GCD}(a_i, a_j) > k$$$?
You have to minimize $$$\frac{a_ia_j}{\text{GCD}(a_i, a_j)}$$$ ($$$i \neq j$$$).
For each $$$k = \text{GCD}(a_i, a_j)$$$, $$$a_i, a_j$$$ have to be multiples of $$$k$$$. Note that, if $$$\text{GCD}(a_i, a_j) = h > k$$$, you end up calculating a wrong value of $$$\text{LCM}(a_i, a_j)$$$, but it doesn't matter because it's never optimal; you will calculate the correct (smaller) value of the $$$\text{LCM}$$$ while considering $$$\text{GCD}(a_i, a_j) = h$$$ .
So, for each $$$k$$$, it's enough to consider the smallest $$$a_i, a_j$$$ that are multiples of $$$k$$$. You can find them like in Solution 1 or Solution 3 (instead of the sum, you should keep the two minimum elements).
agc038_c - LCMs
Once again, use $$$\text{GCD}$$$ instead of $$$\text{LCM}$$$ and solve the problem for each fixed $$$\text{GCD}$$$.
Let $$$\displaystyle g(k) = \sum_{k | a_i, k | a_j, i < j}a_ia_j$$$. Can you calculate it with Solution 1 (or Solution 3)?
Let $$$g_1(k) = \sum_{k | a_i}a_i$$$, $$$g_2(k) = \sum_{k | a_i}a_i^2$$$ (they can be calculated with Solution 1 or Solution 3). Then, $$$g(k) = \frac{1}{2}(g_1(k)^2 - g_2(k))$$$ (it's easy to prove).
Now the problem is that some products $$$a_ia_j$$$ considered in $$$g(k)$$$ may have $$$\text{GCD}(a_i, a_j) > k$$$. How to fix that?
You have to calculate the sum of $$$\frac{a_ia_j}{\text{GCD}(a_i, a_j)}$$$ ($$$i < j$$$).
For each $$$k = \text{GCD}(a_i, a_j)$$$, $$$a_i, a_j$$$ have to be multiples of $$$k$$$. Let's start by calculating $$$\displaystyle g(k) = \sum_{k | a_i, k | a_j, i < j}a_ia_j$$$, then we will remove pairs such that $$$\text{GCD}(a_i, a_j) > k$$$.
Let $$$g_1(k) = \sum_{k | a_i}a_i$$$, $$$g_2(k) = \sum_{k | a_i}a_i^2$$$ (they can be calculated with Solution 1 or Solution 3, using $$$b_i = a_i$$$ and $$$b_i = a_i^2$$$ respectively). Note that $$$\displaystyle g_2(k) = \sum_{k | a_i, k | a_j}a_ia_j$$$. Then, $$$g(k) = \frac{1}{2}(g_1(k)^2 - g_2(k))$$$.
Finally, let $$$\displaystyle f(k) = \sum_{\text{GCD}(a_i, a_j) = k, i < j}a_ia_j$$$. Let's calculate $$$f(k)$$$ for $$$k$$$ from $$$m$$$ to $$$1$$$. Then, $$$f(k) = g(k) - \sum_{i=2}^{\lfloor m/k \rfloor} f(ik)$$$ (it's the same idea as the Solution 1).
abc191_f - GCD or MIN
Suppose you want the last number of the blackboard to be $$$k$$$. Is there an optimal order of operations (such that, if $$$k$$$ can be reached, you can also reach it with that order of operations)?
It's optimal to use all the $$$\text{GCD}$$$ operations before all the $$$\text{MIN}$$$ operations. So, how does the last number of the blackboard look like?
The last number of the blackboard is $$$\leq \min(a_i)$$$, and it's the $$$\text{GCD}$$$ of a subset of $$$a$$$. How to count the possible final numbers?
If $$$k$$$ is the $$$\text{GCD}$$$ of some subset, it's also the $$$\text{GCD}$$$ of $$$S_k = \{a_i \mid k | a_i\}$$$. How to calculate the $$$\text{GCD}$$$ of $$$S_k$$$ for each $$$k$$$?
It's easy to prove that the final number on the blackboard is $$$\leq \min(a_i)$$$, and it's the $$$\text{GCD}$$$ of a subset of $$$a$$$.
For a fixed $$$k$$$, a necessary and sufficient condition for it to be the $$$\text{GCD}$$$ of a subset is to be the $$$\text{GCD}$$$ of the "worst-case" subset, namely $$$S_k = \{a_i \mid k | a_i\}$$$. Let $$$f(k)$$$ be such $$$\text{GCD}$$$.
Initially, all $$$f(k)$$$ are set to $$$0$$$. For each $$$a_i$$$, iterate over its divisors $$$j$$$ (with Solution 2) and set $$$f(j) := \text{GCD}(f(j), a_i)$$$
The answer is the number of $$$k \leq \min(a_i)$$$ such that $$$f(k) = k$$$.
Other problems
1493D - GCD of an Array (suggested by nor)
1436F - Sum Over Subsets (nor)
Codechef — Chefsums (nor)
Conclusions
We've seen that this technique is very flexible. You can choose the complexity on the basis of the constraints, and $$$f(k)$$$ can be anything that can be updated fast.
Of course, suggestions/corrections are welcome. In particular, please share in the comments other problems that can be solved with this technique.
I hope you enjoyed the blog!
Author: TheScrasse
Preparation: MyK_00L
Suppose that you can use $$$x$$$ operations of type $$$1$$$ and $$$y$$$ operations of type $$$2$$$. Try to reorder the operations in such a way that $$$a$$$ becomes the minimum possible.
You should use operations of type $$$2$$$ first, then moves of type $$$1$$$. How many operations do you need in the worst case? ($$$a = 10^9$$$, $$$b = 1$$$)
You need at most $$$30$$$ operations. Iterate over the number of operations of type $$$2$$$.
Notice how it is never better to increase $$$b$$$ after dividing ($$$\lfloor \frac{a}{b+1} \rfloor \le \lfloor \frac{a}{b} \rfloor$$$).
So we can try to increase $$$b$$$ to a certain value and then divide $$$a$$$ by $$$b$$$ until it is $$$0$$$. Being careful as not to do this with $$$b<2$$$, the number of times we divide is going to be $$$O(\log a)$$$. In particular, if you reach $$$b \geq 2$$$ (this requires at most $$$1$$$ move), you need at most $$$\lfloor \log_2(10^9) \rfloor = 29$$$ moves to finish.
Let $$$y$$$ be the number of moves of type $$$2$$$; we can try all values of $$$y$$$ ($$$0 \leq y \leq 30$$$) and, for each $$$y$$$, check how many moves of type $$$1$$$ are necessary.
Complexity: $$$O(\log^2 a)$$$.
If we notice that it is never convenient to increase $$$b$$$ over $$$6$$$, we can also achieve a solution with better complexity.
Official solution: 107232596
1485B - Replace and Keep Sorted
Author: TheScrasse
Preparation: Kaey
You can make a $$$k$$$-similar array by assigning $$$a_i = x$$$ for some $$$l \leq i \leq r$$$ and $$$1 \leq x \leq k$$$.
How many $$$k$$$-similar arrays can you make if $$$x$$$ is already equal to some $$$a_i$$$ ($$$l \leq i \leq r$$$)?
How many $$$k$$$-similar arrays can you make if either $$$x < a_l$$$ or $$$x > a_r$$$?
How many $$$k$$$-similar arrays can you make if none of the previous conditions holds?
Let's consider each value $$$x$$$ from $$$1$$$ to $$$k$$$.
- If $$$x < a_l$$$, you can replace $$$a_l$$$ with $$$x$$$ (and you get $$$1$$$ $$$k$$$-similar array). There are $$$a_l-1$$$ such values of $$$x$$$.
- If $$$x > a_r$$$, you can replace $$$a_r$$$ with $$$x$$$ (and you get $$$1$$$ $$$k$$$-similar array). There are $$$k-a_r$$$ such values of $$$x$$$.
- If $$$a_l < x < a_r$$$, and $$$x \neq a_i$$$ for all $$$i$$$ in $$$[l, r]$$$, you can either replace the rightmost $$$b_i$$$ which is less than $$$x$$$, or the leftmost $$$b_i$$$ which is greater than $$$x$$$ (and you get $$$2$$$ $$$k$$$-similar arrays). There are $$$(a_r - a_l + 1) - (r - l + 1)$$$ such values of $$$x$$$.
- If $$$x = a_i$$$ for some $$$i$$$ in $$$[l, r]$$$, no $$$k$$$-similar arrays can be made.
The total count is $$$(a_l-1)+(k-a_r)+2((a_r - a_l + 1) - (r - l + 1))$$$, which simplifies to $$$k + (a_r - a_l + 1) - 2(r - l + 1)$$$.
Complexity: $$$O(n + q)$$$.
Official solution: 107232462
Authors: isaf27, TheScrasse
Preparation: Kaey
Let $$$\lfloor \frac{a}{b} \rfloor = a~\mathrm{mod}~b = k$$$. Is there an upper bound for $$$k$$$?
$$$k \leq \sqrt x$$$. For a fixed $$$k$$$, can you count the number of special pairs such that $$$a \leq x$$$ and $$$b \leq y$$$ in $$$O(1)$$$?
We can notice that, if $$$\lfloor \frac{a}{b} \rfloor = a~\mathrm{mod}~b = k$$$, then $$$a$$$ can be written as $$$kb+k$$$ ($$$b > k$$$). Since $$$b > k$$$, we have that $$$k^2 < kb+k = a \leq x$$$. Hence $$$k \leq \sqrt x$$$.
Now let's count special pairs for any fixed $$$k$$$ ($$$1 \leq k \leq \sqrt x$$$). For each $$$k$$$, you have to count the number of $$$b$$$ such that $$$b > k$$$, $$$1 \leq b \leq y$$$, $$$1 \leq kb+k \leq x$$$. The second condition is equivalent to $$$1 \leq b \leq x/k-1$$$.
Therefore, for any fixed $$$k > 0$$$, the number of special pairs ($$$a\leq x$$$; $$$b \leq y$$$) is $$$max(0, min(y,x/k-1) - k)$$$. The result is the sum of the number of special pairs for each $$$k$$$.
Complexity: $$$O(\sqrt x)$$$.
Official solution: 107232416
1485D - Multiples and Power Differences
Author: TheScrasse
Preparation: MyK_00L
Brute force doesn't work (even if you optimize it): there are relatively few solutions.
There may be very few possible values of $$$b_{i,j}$$$, if $$$b_{i-1,j}$$$ is fixed. The problem arises when you have to find a value for a cell with, e.g., $$$4$$$ fixed neighbors. Try to find a possible property of the neighbors of $$$(i, j)$$$, such that at least a solution for $$$b_{i,j}$$$ exists.
The least common multiple of all integers from $$$1$$$ to $$$16$$$ is less than $$$10^6$$$.
Build a matrix with a checkerboard pattern: let $$$b_{i, j} = 720720$$$ if $$$i + j$$$ is even, and $$$720720+a_{i, j}^4$$$ otherwise. The difference between two adjacent cells is obviously a fourth power of an integer. We choose $$$720720$$$ because it is $$$\operatorname{lcm}(1, 2, \dots, 16)$$$. This ensures that $$$b_{i, j}$$$ is a multiple of $$$a_{i, j}$$$, because it is either $$$720720$$$ itself or the sum of two multiples of $$$a_{i, j}$$$.
Complexity: $$$O(nm)$$$.
Official solution: 107232359
Author: TheScrasse
Preparation: TheScrasse
What happens if you can't swap coins?
Let $$$dp_i$$$ be the maximum score that you can reach after $$$dist(1, i)$$$ moves if there is a red coin on node $$$i$$$ after step $$$3$$$. However, after step $$$2$$$, the coin on node $$$i$$$ may be either red or blue. Try to find transitions for both cases.
If you consider only the first case, you solve the problem if there are no swaps. You can greedily check the optimal location for the blue coin: a node $$$j$$$ such that $$$dist(1,i) = dist(1,j)$$$ and $$$a_j$$$ is either minimum or maximum.
Instead, if the coin on node $$$i$$$ is blue after step $$$2$$$, the red coin is on node $$$j$$$ and you have to calculate $$$\max(dp_{parent_j} + |a_j - a_i|)$$$ for each $$$i$$$ with a fixed $$$dist(1, i)$$$. How?
Divide the nodes in groups based on the distance from the root. Then, for each $$$dist(1, i)$$$ in increasing order, calculate $$$dp_i$$$ — the maximum score that you can reach after $$$dist(1, i)$$$ moves if there is a red coin on node $$$i$$$ after step $$$3$$$. You can calculate $$$dp_i$$$ if you know $$$dp_j$$$ for each $$$j$$$ that belongs to the previous group. There are two cases:
if after step $$$2$$$ the coin on node $$$i$$$ is red, the previous position of the red coin is fixed, and the blue coin should reach either the minimum or the maximum $$$a_j$$$ among the $$$j$$$ that belong to the same group of $$$i$$$;
if after step $$$2$$$ the coin on node $$$i$$$ is blue, there is a red coin on node $$$j$$$ ($$$dist(1, i) = dist(1, j)$$$), so you have to maximize the score $$$dp_{parent_j} + |a_j - a_i|$$$.
This can be done efficiently by sorting the $$$a_i$$$ in the current group and calculating the answer separately for $$$a_j \leq a_i$$$ and $$$a_j > a_i$$$; for each $$$i$$$ in the group, the optimal node $$$j$$$ either doesn't change or it's the previous node.
Alternatively, you can notice that $$$dp_{parent_j} + |a_j - a_i| = \max(dp_{parent_j} + a_j - a_i, dp_{parent_j} + a_i - a_j)$$$, and you can maximize both $$$dp_{parent_j} + a_j - a_i$$$ and $$$dp_{parent_j} + a_i - a_j$$$ greedily (by choosing the maximum $$$dp_{parent_j} + a_j$$$ and $$$dp_{parent_j} - a_j$$$, respectively). In this solution, you don't need to sort the $$$a_i$$$.
The answer is $$$\max(dp_i)$$$.
Complexity: $$$O(n)$$$ or $$$O(n\log n)$$$.
Official solution: 107232216
Author: TheScrasse
Preparation: TheScrasse
Why isn't the answer $$$2^{n-1}$$$? What would you overcount?
Find a dp with time complexity $$$O(n^2\log n)$$$.
Let $$$dp_{i, j}$$$ be the number of hybrid prefixes of length $$$i$$$ and sum $$$j$$$. The transitions are $$$dp_{i, j} \rightarrow dp_{i+1, j+b_i}$$$ and $$$dp_{i,j} \rightarrow dp_{i+1,b_i}$$$. Can you optimize it to $$$O(n\log n)$$$?
For each $$$i$$$, you can choose either $$$a_i = b_i$$$ or $$$a_i = b_i - \sum_{k=1}^{i-1} a_k$$$. If $$$\sum_{k=1}^{i-1} a_k = 0$$$, the two options coincide and you have to avoid overcounting them.
This leads to an $$$O(n^2\log n)$$$ solution: let $$$dp_i$$$ be a map such that $$$dp_{i, j}$$$ corresponds to the number of ways to create a hybrid prefix $$$[1, i]$$$ with sum $$$j$$$. The transitions are $$$dp_{i, j} \rightarrow dp_{i+1, j+b_i}$$$ (if you choose $$$b_i = a_i$$$, and $$$j \neq 0$$$), $$$dp_{i,j} \rightarrow dp_{i+1,b_i}$$$ (if you choose $$$b_i = \sum_{k=1}^{i} a_k$$$).
Let's try to get rid of the first layer of the dp. It turns out that the operations required are
- move all $$$dp_j$$$ to $$$dp_{j+b_i}$$$
- calculate the sum of all $$$dp_j$$$ in some moment
- change the value of a $$$dp_j$$$
and they can be handled in $$$O(n\log n)$$$ with "Venice technique".
$$$dp$$$ is now a map such that $$$dp_j$$$ corresponds to the number of ways to create a hybrid prefix $$$[1, i]$$$ such that $$$\sum_{k=1}^{i} a_k - b_k = j$$$. Calculate the dp for all prefixes from left to right. if $$$b_i = a_i$$$, you don't need to change any value of the dp; if $$$b_i = \sum_{k=1}^{i} a_k$$$, you have to set $$$dp_{\sum_{k=1}^{i} -b_k}$$$ to the total number of hybrid arrays of length $$$i-1$$$.
Complexity: $$$O(n\log n)$$$.
Official solution: 107232144
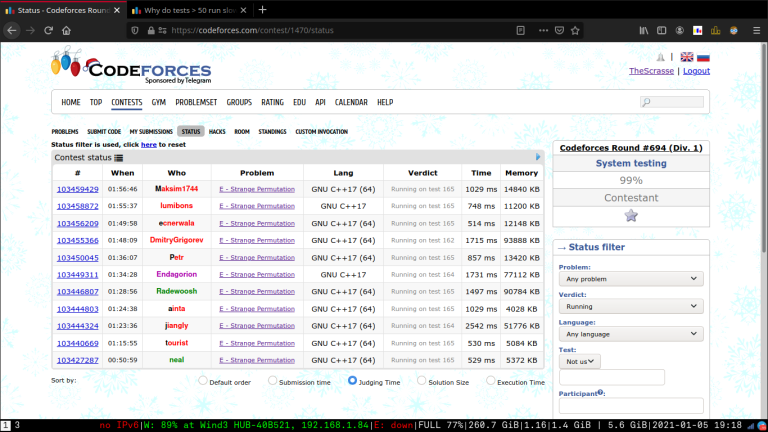
It's quite weird that $$$11$$$ submissions are still running from at least $$$20$$$ minutes, while hundreds of submissions (even with long execution times) are usually evaluated in a few seconds. It seems that the last tests run much more slowly than the other tests. Does anyone know why it happens?
As promised, here are some (nested) hints for Codeforces Round #682 (Div. 2).
1438A - Specific Tastes of Andre
Solve some small tests on paper.
Can you make the sum of each subarray equal to its length?
1438B - Valerii Against Everyone
Suppose that the answer is NO. Which property should hold for the array $$$a$$$?
What happens if $$$l_1 = r_1$$$?
The answer is YES if there is a pair of equal elements in the array $$$b$$$. What happens if there are no equal elements?
Look at the binary representation of the sum of each subarray. Are there equal binary representations?
Solve on paper
3 3
1 1 1
1 1 1
1 1 1
Now solve
3 3
2 1 1
1 1 2
2 1 2
Do a chess coloring on the grid. Can you make all differences odd?
How does the xor of all the array change after every operation?
The xor of all the array remains constant. Let it be $$$x$$$. If you make all elements equal, what's the xor of the resulting array?
If $$$n$$$ is even, $$$x = 0$$$. So the answer is NO if the starting xor is not $$$0$$$.
If $$$n$$$ is odd, you can set $$$a[i] = x$$$ for each $$$i$$$, and their xor is $$$x$$$. The answer is always YES.
In both cases, if the answer is YES, you can solve the problem by making each $$$a[i]$$$ equal to $$$x$$$. Can you make $$$a[1] = x$$$ first?
Now you want to "spread" $$$x$$$ in all the array. You already have some $$$a[i] = x$$$. Are there three indices such that $$$a[i] \oplus a[j] \oplus a[k] = x$$$?
I wasn't able to solve E and F. If you did, you may want to add your hints in the comments.
Also, please send a feedback if the hints are unclear or if they spoil the solution too much.
Hi everyone,
many people are a bit disappointed because, for example, while the most difficult problems of Div. 3 contests are still interesting for Div. 2, Div. 3 contests are unrated for higher divisions. The same argument is valid for Div. 2 and Div. 4 contests.
An idea could be make contests rated for everyone, but that's not the best solution because, to reach a $$$\geq 1900$$$ rating, solving Div. 3 and Div. 4 problems very fast would be enough.
An improvement could be make contests partially rated for higher divisions, that is, the rating variation is multiplied by a $$$k$$$ factor ($$$0 \leq k \leq 1$$$) that depends on the target division of the contest and on the initial rating of the contestant (i. e. the relevance of that contest for that contestant). An example: there's a Div. 2 contest, then $$$k$$$ could be $$$1$$$ for a $$$1900$$$ rated contestant, $$$0.8$$$ for a $$$2100$$$ rated contestant, $$$0.5$$$ for a $$$2200$$$ rated contestant, etc.
Hi everyone, I have just tried to solve the problem 161D.
If I use a matrix dp[50010][510], I get a tle verdict, even if the time complexity of the solution is $$$O(nk)$$$, $$$nk < 10^8$$$ and the constant factors are quite small. But if I use a matrix dp[510][50010] and I swap the indices, I get ac with a time of 498 ms (much less than the time limit).
Why does it happen?
Thanks
Submission with tle verdict: 73781168
Submission with ac verdict: 73781989
| Name |
|---|










