Hi to all!
Today I want to talk a little bit about writing an elegant data structure — Heavy-light decomposition (or just HLD).
Many of you are probably faced with problems like "given a weighted tree, requests for modification edges and queries finding the minimum on the edges between two vertices." HLD can quite easily do this and many other tasks.
Lets begin with a brief description of the structure.
// A more complete description is on e-maxx. (in Russian)
Heavy-light decomposition — this is such a decomposition of graph into disjoint paths at the vectixes or edges that on the way from any node to the root of this tree we will change no more than log(N) paths. If we can build such paths then with the help of additional structures (segment tree (or just ST), for example) we will be able to respond quickly to requests.
We call an edge heavy if son's subtree, to which leads this edge, will be not less than half of the size of the father's subtree. In other words, 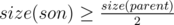 . Note that from the vertix downwards may extend no more than one heavy edge.
. Note that from the vertix downwards may extend no more than one heavy edge.
"And it gives us?" — You ask. And it gives us the following: if we take all the vertices that have not outgoing heavy edge, and we will rise to the root, until it reach or pass by a light edge, then this paths will be paths in HLD.
Constructing a segment tree on each of the ways we can for log2(N) respond to a lot of kinds of requests between two vertices (maximum, etc.). You will need to gently rise from the vertices to their lca (lowest common ancestor) and do requests to ST or something else.
Now about amount of code ..
The first time I tried to write this structure to the problem, the code was, to put it mildly, a rather big. I honestly was looking for lca, honestly built on each of the paths and whatnot. And now there is talk about how to reduce the amount.
About construction of HLD
The first thing to fix, so it's a bit awkward construction. Now in this form, as described above, it is not very comfortable to write.
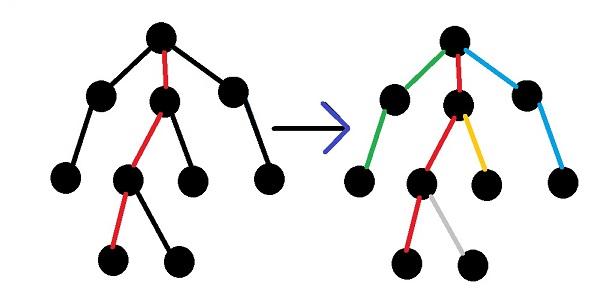
You can build a decomposition as follows: let we are in a vertex. It belongs to a path. Consider all the children of this node — we can continue this way in just one son, but all the other children will be the beginning of new ways. To what son we should continue this way? That's right, to son which has the largest subtree. So one dfs needed to calculate the size of the subtrees and the other for direct construction of decomposition.
About separate structures for each path
Next, I'll talk on an example of ST, since it is often necessary for tasks. The next thought after we learned simple building HLD, I had about this: "Damn, it's still necessary ST for each way to write." Yes, it's not that hard, but for me it was a bit uncomfortable. But then you can see that only one ST needed. Need to renumber the vertices in each path that all the vertices are on the same subsegments (for ST). So we heed only 1 ST.
About finding lca
Another uncomfortable thing — separate finding LCA.
It turns out that we should not look for lca explicitly. Let's proceed to the following algorithm: consider two ways in which our now vertices. If they are on the same path, it's just a request (ST) . And if not? Then let's choose the path that has the highest vertix below. Then just go to the ancestor of this vertex. So we will continue until we come to the same path. Parallel to all these lifts will make requests to ST, thus looking for an answer.
We have that answer to the query and finding lca can be done simultaneously.
Materials
I am very grateful to the site e-maxx, which has a good description (tap) of this structure. I relied a lot on this article.
Another good materials here.
And a short realization is here
Bonus
You can check your HLD on this problem. And here is my code.
Another problems: QTREE, Aladdin and the Return Journey.
P.S. I understand that the simplicity of the structure — relative thing. I tried to explain how it's easy to write for me. I'll be very happy if this article will be useful.
P.P.S This is my first article. I will be glad to hear constructive criticism, comments about the article.










