These days (26.-27.3.2015), another national round of Slovak Olympiad in Informatics took place. Just short problem statements for now, I'll write it in more detail and with solutions later:
1.
There's a hazelnut chocolate of size N × M, which can be viewed as a 2D grid. In each cell of the grid, there's a given number of nuts. Two players play a game, alternating turns: each player has to cut off either the bottom row or the rightmost column of the remaining part of the chocolate in her turn (and do with it guess what). The cut off row/column has to contain an even number of nuts. The player that can't make a move loses. Determine the winner if both play optimally.
2.
You have two numbers N, K ( ), one input file with N - K distinct numbers between 1 and N and 2K + 2 empty files. Find the missing K numbers.
), one input file with N - K distinct numbers between 1 and N and 2K + 2 empty files. Find the missing K numbers.
Your program has a very limited amount of memory (the files' content isn't stored in that memory), just 10 kB for K ≤ 100; its memory complexity can't depend on N. Primarily, you need to minimise the worst-case number of reads+writes to files; only then are you minimising the time and memory complexity of your algorithm.
Files work like queues and can be erased in small constant time.
3.
a very long introductory text and some heavily theoretical magic with simulating boolean conditions using other conditions and proving that it's always possible/impossible
4.
There are N numbers up to 109 and another number R, also up to 109. Find up to 4 numbers (one number can't be used multiple times) among these N that sum up to R or decide that they don't exist. N ≤ 4000.
5.
There's a straight river of constant width, N points on one side of it and M on the other side. You need to connect some of them with (obviously straight) lines that have the minimum total length in such a way that each of these N + M points has at least one line connecting it with another point on the other side of the river. N, M ≤ 20000.
The first 3 problems are theoretical (points for explaining your algorithm), the other 2 practical (typical contest style, partial scoring); the max. time limit was 10s in both.









 .
.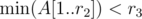 . Based on the answer, we can decide whether to add him to the shortlist. Then, we need to add the currently processed engineer by updating
. Based on the answer, we can decide whether to add him to the shortlist. Then, we need to add the currently processed engineer by updating 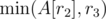 .
. , so we have an
, so we have an 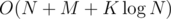 , because all but the query answering/updating takes just linear time and a segment tree can be constructed in
, because all but the query answering/updating takes just linear time and a segment tree can be constructed in 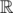 , so its maxima must satisfy
, so its maxima must satisfy 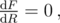
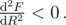
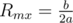 , with the corresponding maximum
, with the corresponding maximum 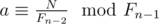 (think why it's equivalent to N=F_{n-1}b+F_{n-2}a$)
(think why it's equivalent to N=F_{n-1}b+F_{n-2}a$)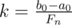 (integer division). If
(integer division). If  factorisation for
factorisation for 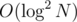 complexity per query with
complexity per query with 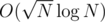 precomputation.
precomputation.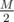 correct answers and count how many of them each student answered correctly, as a vector
correct answers and count how many of them each student answered correctly, as a vector 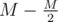 answers, obtaining vectors
answers, obtaining vectors 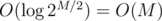 ), so the time for this is
), so the time for this is 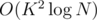 and a horrible constant. If there's a better solution, write it in the comments.
and a horrible constant. If there's a better solution, write it in the comments.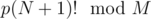 , where
, where 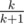 and the probability of not picking one is
and the probability of not picking one is  , the answer is (
, the answer is (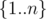 )
)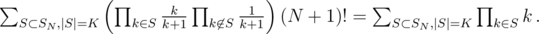
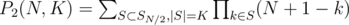
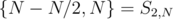 .
.  , the sum would obviously be just
, the sum would obviously be just 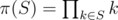 .
.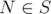 , we only need
, we only need  disjointly and uniquely into
disjointly and uniquely into 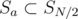 and
and  .
. 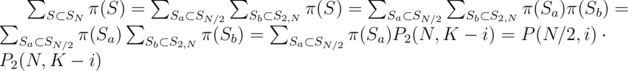
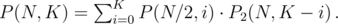
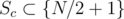 . We have 2 choices for
. We have 2 choices for 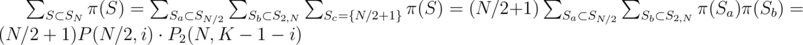
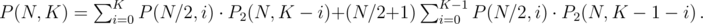
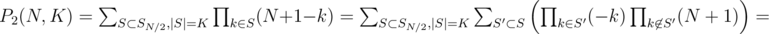

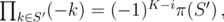
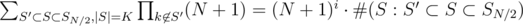
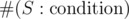 denotes the number of sets
denotes the number of sets 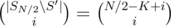 , so
, so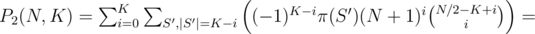
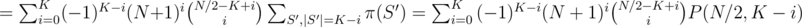
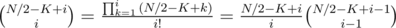
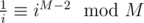 .
.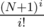 , which saves us some modulo operation compared to precomputing
, which saves us some modulo operation compared to precomputing 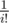 separately.
separately. 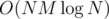 time. This is basically problem
time. This is basically problem 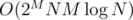 , which isn't particularly great.
, which isn't particularly great. of vector
of vector 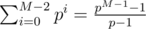 (you don't have to calculate that, just take the difference of hashes of
(you don't have to calculate that, just take the difference of hashes of 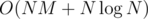 time (the whole algorithm now takes
time (the whole algorithm now takes 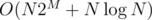 time). Afterwards, we can easily check if some interval contains at least
time). Afterwards, we can easily check if some interval contains at least  , where the sums for all subsets can be pre-computed.
, where the sums for all subsets can be pre-computed.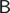 from each of the 4 possible directions. This time, stop when it starts to loop (including hitting point
from each of the 4 possible directions. This time, stop when it starts to loop (including hitting point 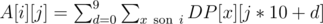 for 3-digit numbers
for 3-digit numbers 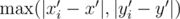 , and the region for which it's
, and the region for which it's 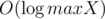 time and the sorting takes
time and the sorting takes 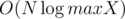 . With
. With 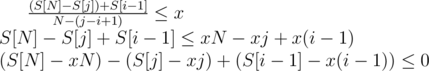
 , and similarly for array
, and similarly for array 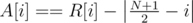 ,
, 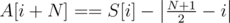 and sort it. If we subtracted
and sort it. If we subtracted 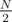 letters for all ways of picking those
letters for all ways of picking those 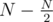 letters.
letters.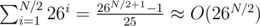 .
.
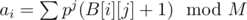 , where
, where 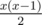 for all
for all 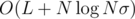 (
(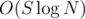 , because comparing vectors takes up to
, because comparing vectors takes up to 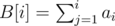 . Then, we're looking for all pairs
. Then, we're looking for all pairs  hits. Watch out for the case
hits. Watch out for the case 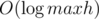 such checks, and one check can be done in linear time, so the total time is
such checks, and one check can be done in linear time, so the total time is 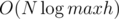 .
.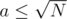 , so we can try all
, so we can try all 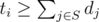 .
.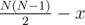 .
.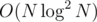 time, but that's way too ugly to implement.
time, but that's way too ugly to implement. , I chose 500 for this case) and make an 2D Fenwick tree
, I chose 500 for this case) and make an 2D Fenwick tree 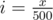 and
and 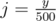 (integer division); its dimensions are then just 400x400.
(integer division); its dimensions are then just 400x400.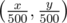 in our BIT (Fenwick tree). And that's just 1 query. The updates are even simpler: set
in our BIT (Fenwick tree). And that's just 1 query. The updates are even simpler: set 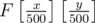 .
.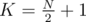 (division is classical integer division here) must be the supporters.
(division is classical integer division here) must be the supporters.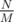 ;
;  groups to be won. There's no point in sending any supporters of
groups to be won. There's no point in sending any supporters of 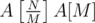 .
.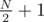 for
for 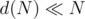 — it's something like
— it's something like 
