A. Arrangement of RGB Balls

(difficulty: easy)

If, among 3 consecutive balls, there are no two of the same color, then there's exactly one ball of every color among them. Thereforce, the sequence is determined by the order of the first 3 balls. Imagine these are RGB; then, the sequence continues as RGBRGBRGB...

There are only 3! = 6 possible initial triples, so we can try all the sequences defined by them, and for every one of them, check if it can be constructed. When is it possible to construct such a sequence? Take the initial triple to be "GRB", for example (the idea for other triples is analogous). It's clear that the sequence is "GRB" repeated some K times, and after that, there are the first 0, 1 or 2 balls from that triple (for example, "GRBGRBGR" or just "G"). It's clear that K = min(R, G, B). So it's possible to construct iff 1 ≥ G - K ≥ R - K ≥ B - K.

Testing the existence of any sequence can be done in O(1) time like this. There are O(1) possible initial triples, so the time per test case is O(1).

Bonus: The problem is more interesting if we allow N colors, also with the condition of any N consecutive ones distinct. We don't actually have to try all possible initial triples :D

B. Bentago

(diff: medium)

Let's recall some terms from the game theory. A position is a state of the game, in this case represented (in the simplest form) by a 4x4 array of free spaces, white and black balls. Every position is either winning (W) or losing (L). A losing position is one in which the opponent's marbles lie on a line (the opponent won), and also a position, from which there's no way to get to an L position. The rest of the positions (it's possible to get to an L one) are winning. Notice that for any finite game (as is ours, as the number of marbles on the board increases in every turn), the graph of positions is a DAG, so it's possible to traverse it and compute for every position its state (W or L).

In this game, we also add draw positions, D. Those are the final draw positions (when both players have marbles on a line), and also those that aren't W, but it's possible to get to a drawing one (the player whose turn it is doesn't have a sure way to win, so he's content with a draw). It's just a minor upgrade to the standard combinatorial games, and doesn't affect the problem much.

The board is really small, so we should use that to our advantage. If there are not many positions in total in the game, we could do exactly the mentioned DAG traversal from the current position, and compute its state.

First, we need to know if that's even possible, so let's count how many positions there are in total. Let's consider a position after 2K turns. There are 2K marbles on the board, K of every type. How many such boards are there? We have 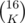ways of placing black marbles, and 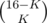ways of placing the white ones afterwards; 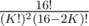. Similarly, if there are 2K + 1 marbles, we have 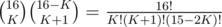possible positions. Summation over all K (up to 8 for 2K, up to 7 for 2K + 1, since the game doesn't take any longer) gives the total number of positions to be around 10⁷.

That's not too much to list (in fact, we could represent them as a 3-based number), but if we consider that there are 8 possible rotations of the board and N - 2K( - 1) ways of placing the marble, there are a bit too many edges in the DAG (for 2K = 10, it's 64 edges from each of the 2·10⁶ positions). To improve that, we double our positions by taking "half-positions", which are positions after a player adds a marble, but before rotating the board. There are at most 8 edges leading from most positions now, and we just doubled our memory.

This leaves us with at most around 160 million edges in the graph. Drawing every move could get lengthy as well, so we could denote the empty spaces in any position in binary, and pre-compute all powers of 3 in order to transform a (3-based) position into a half-position with a marble added in O(1). Next, we could pre-compute the 3-based represenations of all 4 subboards, the subboards that we get to from them by both rotations, and remember, for every position, the sum of which 4 subboards it is. Then, rotating a subboard is just subtracting the rotated one and adding the one to which it was rotated, in O(1).

Another optimization is not traversing the whole DAG. Just do it from the starting position, and stop going deeper when you find a final position. Also, keep the whole graph for all test cases; when you see that the starting position in a particular test case has been traversed before, you know the answer directly (and you don't need to go deeper from already known positions).

The whole problem has an O(1) approach, but it's heavily optimization based. I haven't coded my ideas yet, but I believe it's (with a bit more optimization, possibly) a basis of a successful solution :D

C. Combination Lock

(diff: easy)

We're given a sequence A. The task asks us to find a permutation P of elements of set {1..N}, such that the sequence B (B[i] = (A[i] + P[i] - 1)%N + 1) is another permutation of {1..N}. In other words, we need to decide whether there exist 2 permutations such that if we subtract every element of one of them from the corresponding element of the other, we'll get a sequence equal to A (with all elements taken modulo N).

It's clear that the answer is NO, if 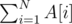isn't divisible by N, because the sums of elements of both permutations are equal, and the sum of differences must be equal to that, which is .

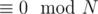It's worth a try to assume the condition is sufficient as well as necessary. After trying to submit a program that just checks if the sum of A is divisible by N, we get AC :D. The time complexity of this approach is O(N).

I hope to find a proof soon. I'll write it when I do.

D. Dreamer Land of Kashan

(diff: easy-medium)

We're given an undirected simple graph. We want to make it connected by moving and adding some edges. There are several key observations to be made:

1. If the cost of moving an edge is  > c, it's better to not move it, and instead add an edge. It's cheaper.

2. If (possibly after several other operations) we're moving a bridge — an edge whose removal split a connected component into 2, it's better not to move it, because we'd need to connect those 2 components again, and we could place the edge we'd otherwise use for that, in place of the bridge we'd move. For example, if the edges of our graph are (1,2) (2,3) and there's also an isolated vertex 4, it's more expensive to move edge (1,2)->(3,4) and add an edge (1,3), than to just add an edge (3,4). In other words, every moved edge can't be a bridge, and must be moved as to connect 2 distinct connected components.

3. If an edge is not a bridge and it has cost exactly c, it's better to move it than to add an edge. The cost is the same, but there's one less added edge.

Let's say we have C connected components. We can remove M - (N - C) edges so that the connectivity of the graph (the vertices in its connected components) doesn't change, because we have left C trees with N vertices in total, and a tree with K vertices has K - 1 edges. Then, we can choose as many edges (starting from the cheapest one, and only those with cost  ≤ c) as possible for connecting as many components as necessary, and then add some edges to connect the remaining conn. components. Of course, we want these edges to be the cheapest ones — we can't choose bridges anyway, and from every cycle, we remove the cheapest edge (which doesn't change connctivity), so we can just go greedily. But we need to do it efficiently.

To determine those edges, we can use a simpler version of Disjoint set Union-Find algorithm. First, we sort the edges by non-increasing cost. We store the list of vertices belonging to every component (at the start, every vertex forms a conn. component alone) and the component every vertex belongs to, and keep adding the edges. If an edge we're adding connects 2 already connected vertices, we can take it into the list of edges to be moved instead. Otherwise, it's a bridge (in the graph we have so far), and it's best to add that edge — we take the smaller of those conn. components, move every vertex from it to the larger conn. component, and re-label the component of those vertices to the larger one. Counting the number of currently existing components is easy, too — at the start, C = N; if we connect 2 of them, we decrease C by 1.

When we've found the "removable" edges, the rest is just straightforward greedy (we're adding at most C - 1 edges to connect all C components). Since we change the component of a vertex at most 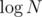times (every time we do it, it gets to an at least 2x larger component), the Union-Find takes 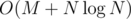time total; the greedy moving/choosing of edges takes O(N), so together with sorting edges, the complexity is 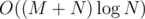per test case.

E. Era of Winter Triangle

(diff: easy-medium)

Let's denote the triangle's vertices as A, B, C and the center of the circle as S. A point is a pair of integer coordinates (a pair of points P,R defines a 2D vector 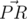, as in physics), so we can find vector cross product (VCP) ; its absolute value is equal to 2x the area of triangle PRT, and its sign determines if T lies on one (> 0) or the other (< 0) half-plane from line PR (not including the line), or on the line PR (== 0). Also, Pythagorean theorem allows us to caculate the (integer) squared distance of 2 points.

This problem takes a lot of casework, just as geometry always does. The cases are:

1. S lies inside triangle ABC, so the answer is YES. In other words, S lies in the same half-plane from line AB (including the line) as point C, in the same half-plane from AC as B, and from the same half-plane from BC as A. The first condition isn't valid only if the VCP of 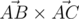and 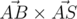is negative; the other 2, analogously.

2. S lies outside the triangle, and S is further than R from the lines AB, BC and AC. Then, the answer is clearly NO; for the answer to be YES, the circle must intersect one of the edges of the triangle or be inside it, but if it's too far, that's impossible. The distance from line AB is also the S altitude of triangle ABS, which is also 2x the area of ABS / distance of A and B. (We can rewrite the inequality to keep our calculations on integers.) So we also check these conditions for all 3 lines AB, BC, AC.

3. The distance from 2. is small enough for some line (let's say it's for AB). There are still 3 possible cases: 1. the feet of said altitude intersects line segment AB, 2. it doesn't, but the circle contains vertex A or B, 3. neither of those things is valid, so the circle doesn't intersect the line (AB).

Condition 1. is equivalent to angles SAB, SBA not being obtuse, which is in turn equivalent (from the law of cosines) to |SA|² + |AB|² - |SB|² ≥ 0, |SB|² + |AB|² - |SA|² ≥ 0.

Condition 2. is easy. Just check if one of the distances |SA|, |SB| is  ≤ R.

This way, we can check (large) case 3. for all 3 lines; if we find an intersection with one of the sides of ABC (or large case 1. is true), the answer is YES; otherwise, it's NO. Time: O(1).

F. Find The Problem!

(diff: easy)

It's clear that all it asks us to do is format a list into a table. There's not much to say, the problem was more tricky in requiring you to print a correctly formatted table. The approach I used is constructing the borders of cells first (all cells are 1x3 characters large, which simplifies things), and writing the entries afterwards.

The rows and columns have to be sorted. For that, we could use maps for row labels, column labels and pairs (row,column)->entry, but the total worst-case complexity is O(N²) (if there are N/2 rows and N/2 columns).

G. General Sohrab & General Sepehr!

(diff: medium)

The main idea for this problem is: every update query can only affect at most 3 pairs.

We could remember all standing soldiers in a set and the directions the soldiers are facing. In addition, for every soldier that's facing right, we remember if the first soldier to his right is facing left (e.g. if he's in a strong pair). In order to make answering queries faster, we remember those entries as "1"s in a BIT (Fenwick tree), which works like an array that can add a number to an element and answer the sum of a range of elements quickly — in time.

At the beginning, we traverse the initial formation of soldiers; all strong pairs are formed by neighboring soldiers, so if soldiers i and i + 1 form a strong pair, we add 1 to BIT[i].

Firstly, queries of type 3. We can count the number of strong pairs that have the left soldier in the given interval, as a query in our BIT for the sum of BIT[L..R]. There can be at most 1 strong pair that we counted and shouldn't have: if the last standing soldier in our interval is facing right and the first one standing to his right is facing left. These soldiers can be found with a simple upper_bound() and we can check in S if it's true. So we can answer in time.

Now, type 1 queries. Let's denote i, j, k our soldier, the first one standing to his left and right, respectively. If i was sitting, he stands up; if (j, k) formed a strong pair, they don't anymore, but (j, i) and (i, k) can become strong pairs. Check these 3 possibilities and remove/add strong pairs (subtract/add 1 in entries of BIT). If i was standing, it's similar, just that (j, k) can become a strong pair instead, and (j, i), (i, k) can become such. That's also time, because we only use a few functions of set<>.

Last, type 2 queries. If the soldier is sitting, we just change his state in S and move on; no strong pairs are affected. Otherwise, (j, i) and (i, k) (in the previously defined notation) are affected — if (j, i) wasn't a strong pair, it becomes one; otherwise, it stops being one, and similarly for (i, k). After checking all these possibilities, we flip the state of soldier i in S. That can also be done with functions of set<> only, in time.

Total time complexity is clearly 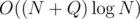per test case. Of course, if some soldier (like, first one standing to the right) doesn't exist, we skip all steps involving him.

K. Killer challenge

(diff: medium)

We don't have a decent way of choosing the largest GCD, but we could use the fact that P is a product of distinct primes. We could mark every interval [i, j) of sequence A with the bitmask, denoting (by 1s) the primes which divide P and 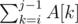; the GCD is equivalent to bitwise OR of 2 bitmasks.

Then, we could use dynamic programming to determine DP[i][x]: the smallest number of cuts necessary to split the first i elements of the sequence into subsequences, whose bitmask OR is equal to x. If an interval [i, j) has bitmask B[i][j], we can move to the state DP[i][x] to states DP[i + k][x|B[i][k]] (indexing from 0 here), so the formula is DP[i + k][x|B[i][k]] = min(DP[i + k][x|B[i][k]], DP[i][x] + 1).

By trying all divisors of P up to 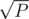(and dividing P by every found divisor, because we need the next one to be a prime, too), we could list all (up to 7, because 2 * 3 * 5 * 7 * 11 * 13 * 17 * 19 = 1·10⁷, roughly 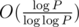, so there are 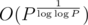bitmasks) prime divisors of P. Then, we could try all those divisors, all subintervals of A, and count B[i][j] in 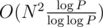time. And finally, try all bitmasks, for every one of them find the GCD it corresponds to, take the largest one and the DP result corresponding to it.

The DP takes O(N) time per state, so 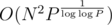total time, and the whole algorithm takes 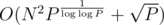time.

I. ICPC Team Selection

(diff: medium-hard in given constraints, hard optimal solution)

Every candidate is a pair of numbers (t_i, r_i) (time of registration, rank); we want to count the number of teams he can be in T_i; then, the answer for this participant is .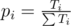

We're only interested in relative order of t_i and r_i, so we can compress then to both range in [0, n), without affecting the order. We do that by adding them to an STL map and then processing the elements of the map in sorted order; that way, we can get their relative order.

First, let's count the number of teams in which i is a newbie, T_0, i. Sort the participants by r_i in decreasing order. Let's process them in this order. For every participant, T_0, i is the number of pairs (j, k) of already processed participants such that t_i > t_k > t_j, r_k > r_j( > r_i) (we assume t_i to be all distinct, too). Member j is experienced and k is wild here.

We don't have a decent way of counting that directly. But we could use the fact that for every pair (k, j) with r_k > r_j, either t_k > t_j or t_k < t_j. And we can count the second type of pairs. To be exact, if there are K_i participants that have larger rank and smaller registration time than participant i, then these are all candidates for experienced member, and for participant j, there are K_i - 1 - 2K_j candidates for wild member (who has to have rank and experience better than the newbie, and can't have them both better than the experienced member; notice that those who have both rank and experience between newbie and experienced are not mentioned here, but by inverting the roles experienced/wild in such a pair, we get a pair where wild has both stats better than experienced; hence 2K_j as we count every such pair again). In total, it's 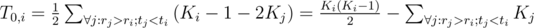. Notice that we divide by 2 there — that's because those pairs are unordered (if we flip the experienced and wild member, we get a pair that's also counted, but invalid).

How do we count that all? The trick here is using a BIT for counting K_i: when processing participant i, we only need to count already processed participants with t_j < t_i, which is a well known problem of counting inversions — we have BIT[t_j] = 1 if we've processed some j with this t_j before, and 0 otherwise; then, K_i is the sum of BIT[0..t_i]. And again, we use BIT for counting the sum of K_j: we have BIT[t_j] = K_j if we've processed the j with t_j before, 0 otherwise, and are asing for the sum of BIT[0..t_i].

That way, T_0, i can be counted in time, with O(1) queries/updates on BIT-s for every participant.

Next, we should count the number of teams in which i is wild. Let's sort and process the participants by increasing rating now. The answer then is the number of pairs of participants (j, k) such that r_j < r_k( < r_i) and t_k < t_i < t_j.

Again, there's no direct simple way of computing that. But if we could count a — the number of pairs which satisfy just r_j < r_k < r_i, t_k < t_j; b — out of those in a, the number of pairs where t_j < t_i, and c — where t_k > t_i, we'll know that the answer is a - b - c (we split the pairs in a into those with t_i in 3 disjoint intervals; 2 of them are counted in b and c, and we're interested in t-s in the last one).

We could count a and c using the same BIT idea as when counting K_i and sum of K_i in the newbie part. To be precise, let's denote the number of participants y such that t_y > t_x and r_y < r_x as L_x and count it in the same way as K_i; a is the sum of L_x for all t_x and c only for t_x > t_i.

The problem is finding b. Let's denote the number of participants with t_y < t_x and r_y > r_x as Q_x (notice that while the definition is similar to that of K_x, the order in which we process the participants is different, so it can't be counted the same way). Unlike K_i and L_i, which don't change when processing other participants, Q_i can change. In particular, it's zero when we process i, and increases by 1 every time we process a participant with a smaller registration time (more experienced) than t_i. So we need to be able to increase all Q_j of processed participants with t_j < t_i efficiently, and also ask for b, which is the sum of all Q_j with t_j < t_i.

If we only had to increase all Q_j in the given interval, this would become a simpler lazy interval tree problem. But we need to only increase for selected participants. That can be done with an advanced lazy interval tree. In node i, we not only remember the sum of Q_j in the interval 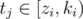and the sum d_i of numbers by which we've increased all Q_j in that interval, but also the number of processed participants pr_i with t_j in that interval. Then, we have 2 types of updates and 1 type of query:

1. UPD1(pos): participant on position "pos" is being processed. Traverse the tree, and update the sum of Q_j in all nodes where pr_i changes (since it's just 1 position, these nodes form a path and there's no need for lazy-loading on pr_i), and update those pr_i afterwards.

2. UPD2(st,end,val): increase all Q_j in the interval of 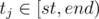by val. Again, traverse the tree normally, update the sum of Q for all traversed nodes, and if a node contains a subinterval of [st, end), all pr_i Q-s in it are increased by val each, so just add val to d_i and don't go deeper into the subtree. Re-update all sums of Q in every processed node that's not a subinterval of [st, end) — after processing its subtree, take the sum of the sums of its sons.

3. QUERY(st,end): get the sum of Q_i for t_i in the given interval. That works the same way as common lazy-loaded interval tree updates. Just don't forget to update the sum of Q-s in all traversed nodes, and not go deeper from a node that's a subinterval of [st, end).

Note: "traverse the tree" is the usual stuff we do including all the return-s when doing something in an interval tree. Updating sum of Q_j is done like this: add pr_i·d_i to the sum (added to the so far every processed participant in the interval), add d_i to d-s of its sons, and set d_i to zero again. It must be done before updating pr_i, because the addition happened before that participant was being processed. I won't explain why this is done in an interval tree here, you can find that elsewhere.

We know how to count b now, so we can count T_1, i for every i. In order to count T_2, i (the number of teams in which one's experienced), we could just swap all pairs of (t_i, r_i) and copy-paste the code for T_1, i.

Finally, it's the end. This solution works in , but it's crazy complicated. And given the constraint N ≤ 5000, I'd believe O(N²) per test case was the intended solution — that's one where we use regular arrays instead of BITs and the mad interval tree. (Maybe a well written 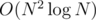would also pass, but that's not really necessary.) I wanted to do an efficient solution, at least.

Bonus (not too difficult): there are N tuples, each with K parameters; every parameter is a permutation of numbers 0..N - 1. Count the number of tuples from which there's no tuple better in all K parameters. (Case K = 3 is especially interesting.) I was reminded of that problem when solving I.

L. Lexicographically Minimal Poem

(diff: easy-medium in given constraints, medium-hard optimal solution)

First, it's better to convert the code to a de-code (if code[i] = j, then decode[j] = i), which will also be a permutation.

If we want the lexicographically minimal poem, we need to minimize the first character. During decryption, we always change this character c to the one pointed by decode[c]. By repeating this, we must sometimes get to a cycle. Decrypting this character to d, which we got to as the i-th on the cycle of length l (i = 0 for c = d), is equivalent to the condition "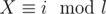" (l consecutive decryptions decrypt all the characters of this cycle back to themselves).

If we're minimizing the first character, it's fine to take the smallest d; the congruence will always be satisfied. We already know how the whole cycle will be decrypted: every character is decrypted to the one that we get to after moving from it i times in the cycle.

Keep going though all characters of the ciphertext; skip those that we can already decrypt, and do the same as above for any character you find not yet decrypted. And remember all the congruences found till now.

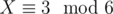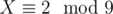It can happen that the congruence corresponding to the minimal solution for some character we're minimizing is inconsistent with some earlier one (for example, and — the first one says that X is divisible by 3, the second one that it's not). Therefore, we need to sort the possible congruences by increasing character after decryption; it's still best to go greedily and choose the smallest congruence that's consistent with all the previously found ones.

When does an inconsistence happen for pairs (a_i, l_i) and (a_j, l_j) (e.g. 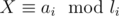and likewise for j)? Firstly, realize that congruence i claims X to be divisible by 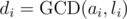, and leaves a congruence 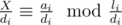. So we could consider any solution X to be a multiple of the solution of the remaining congruences, which have 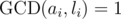. Let's just focus on pairs of individual congruences; then, we'll show that such pairwise consistence is sufficient for existence of a solution.

Let's take i = 1 and j = 2; 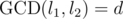; l₁ = dk₁ and l₂ = dk₂. Any solution X can be written as X = dk_1k2A + l_1B + l_2C + D. Modulo l₁, we have X ≡ a₁ ≡ l_2C + D, so l_2C ≡ a₁ - D. But we know that the left side of this congruence and l₁ are divisible by d, so a₁ - D must be, too. Similarly, we get 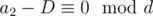, and after subtracting one congruence from the other, we get . If this condition doesn't hold, we have a new inconsistence. Otherwise, we could take D = a₁%d, and our congruences become (after dividing by d) 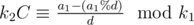, where C can be calculated (for k₁, k₂ coprime) by Euler's totient theorem as 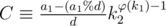; similarly, we could compute B. Nobody cares about A, we could set it to 0. We see that there's a solution (defined by B, C and D) that obviously satisfies the individual congruences.

We haven't shown still that pairwise consistence implies the existence of a general solution. But we can always combine two consistent congruences into one — the two from the previous paragraph to 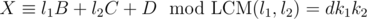. The GCD of this modulus and any other (l₃ for example) is 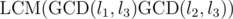, and we need to test whether it divides l_1B + l_2C + D - a₃. But both arguments of the LCM divide it, because it goes back to the original congruences — , so 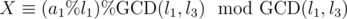, and similarly for l₂; and if both arguments of the LCM divide the number, then so will the LCM. When merging more congruences this way, the GCD(LCM of some l-s, another l) is still just the LCM of individual GCDs, and modulo every one of those, any congruence for X will revert to one of the original ones, and we've checked the pairwise consistence already.

Back to the algorithm. We process the permutation's cycles in order defined by the input string; for every cycle, we try choosing the correct congruence by increasing character, and test if we can choose it by checking the consistence with previously chosen ones. Luckily, as every cycles provides us with congruences of the form 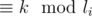for all 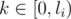, we can always choose at least one (let's imagine it as computing X from the previous congruences, taking X%l_i and choosing the congruence with such k; it's clear that this congruence must be consistent), so the program always works correctly.

What complexity does this approach have? There are only 26 letters in the permutation, so there can be at most 26 cycles and congruences; for every one of them, we only need to check all the possible results of this congruence with all the previous ones, which is O(26²) = O(1). The string only gives the order in which to process the cycles, so we just need to read and process it once, giving time O(N).

UPD: It turns out the smallest solution of any given system of equations (if it exists) is at most 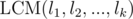, which is (http://oeis.org/A000793) at most around 1000. That means it's possible to check if a system of congruences is valid by trying all possible solutions and checking if a solution satisfies those conditions. And the number of systems of congruences to obtain is also small enough (l₁·l₂·...·l_k), so we could just bruteforce through all of them and choose the lexicographically smallest one. Thanks to savinov for this idea!

Codes

A, C, D, E, F, G, I, K, L

More to be added. That's all I can do in a day...

UPD: code of G added (I had to debug it); started the editorial for I

UPD2: slightly changed difficulty estimates, complete editorial for I

UPD3: updated the editorial of L... another problem that didn't require full optimization (kind of a good thing)

UPD4: editorial for L complete

UPD5: code for optimal solution of I now available; editorial for B added; J coming eventually