Большое спасибо Seyaua за помощь с переводом разбора.

Div. 2 A — Витя в деревне

Идея: _XuMuk_.
Разработка: _XuMuk_.

Нужно аккуратно разобрать несколько случаев :

1. a_n = 15   —  ответ всегда DOWN.

2. a_n = 0   —  ответ всегда UP.

3. Если n = 1   —  ответ -1.

4. Если n > 1, то если a_n–1 > a_n   —  ответ DOWN, иначе UP.

Итоговая асимптотика: .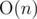

Div. 2 B — Анатолий и тараканы

Идея: _XuMuk_.
Разработка: _XuMuk_.

Заметим, что у нас может быть только две конечные раскраски, удовлетворяющие условию задачи: rbrbrb... или brbrbr...

Переберем раскраску, в которую мы хотим превратить нашу шеренгу.

Посчитаем количество рыжих и черных тараканов, стоящих не на своих местах. Пусть эти числа x и y. Тогда очевидно, что min(x, y) пар тараканов нужно поменять местами, а остальных   —  перекрасить.

Другими словами, результат для фиксированной раскраски   —  это min(x, y) + max(x, y) - min(x, y) = max(x, y). Ответ на задачу   —  это минимум среди результатов для первой и второй раскрасок.

Итоговая асимптотика: .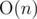

Div. 1 A — Ефим и странная оценка

Идея: BigBag.
Разработка: BigBag.

Заметим, что оценка будет тем выше, чем в более старшем разряде мы ее округлим. Используя это наблюдение, можно легко решить задачу методом динамического программирования.

Пусть dp_i   —  минимальное время, необходимое для того, чтобы получить перенос в (i - 1)-й разряд.

Пусть наша оценка записана в массиве a, то есть a_i   —  i-я цифра оценки.

Существует 3 случая:

1. Если a_i ≥ 5, то dp_i = 1.

2. Если a_i < 4, то dp_i = inf (мы никак не сможем получить перенос в следующий разряд).

3. Если a_i = 4, то dp_i = 1 + dp_i + 1.

После того, как мы посчитали значения dp, нужно найти минимальное pos такое, что dp_pos ≤ t. Так мы узнаем, в какой позиции нужно округлять наше число.

После этого нужно аккуратно прибавить 1 к числу, образованному префиксом из pos элементов исходной оценки.

Итоговая асимптотика: .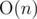

Div. 1 B — Алена и ксероксы

Идея: _XuMuk_.
Разработка: BigBag.

Появится позже.

Div. 1 C — Саша и массив

Идея: BigBag.
Разработка: BigBag.

Вспомним, как можно быстро находить n-e число Фибоначчи.

Для этого нужно найти матричное произведение: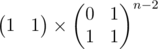

Чтобы решить нашу задачу, заведем следующее дерево отрезков: в каждом листе, соответствующему элементу i будет храниться вектор 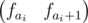, а во всех остальных вершинах будет храниться сумма всех векторов, соответствующих данному отрезку.

Тогда для выполнения первого запроса нужно домножить все векторы на отрезке от l до r на 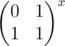, а для ответа на запрос просто найти сумму всех векторов от l до r. Обе эти операции дерево отрезков умеет выполнять за .

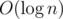Итоговая асимптотика: .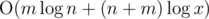

Div. 1 D — Андрей и задача по химии

Идея: _XuMuk_.
Разработка: BigBag.

Поймём как решать задачу за :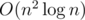

Выберем вершину, к которой мы будем добавлять еще одно ребро. Подвесим дерево за эту вершину. Проставим каждой вершине v_i метку a[v_i] (какое-то число) так, что вершинам с одинаковыми поддеревьями будут соответствовать одинаковые метки, а разным – разные.

Это можно сделать следующим образом: Заведем map<vector<int>, int> m (т.к. максимальная степень вершины 4 — длина вектора всегда будет равняться четырем). Теперь m[{x, y, z, w}] будет хранить метку для вершины, у которой сыновья имеют метки x, y, z, w. Отметим, что вектор нужно хранить в отсортированном виде, а также если сыновей меньше 4, то отсутствующим вершинам ставим метку  - 1.

Давайте поймем, как можно посчитать метку для вершины v. Посчитаем рекурсивно метки для ее сыновей v₁, v₂, v₃, v₄. Тогда если m.count({a[v1], a[v2], a[v3], a[v4]}), то в вершину v нужно поставить соответствующую метку, иначе   —  первое еще не использованное число, т.е. m[{a[v1], a[v2], a[v3], a[v4]}]=cnt++.

Теперь выберем другую вершину, к которой будем добавлять еще одно ребро. Подвесим дерево за эту вершину и расставим метки, при этом не обнуляя счетчик (cnt). Затем проделаем эту операцию со всеми возможными корнями (n раз). Теперь поймем, что если корням соответствуют одинаковые метки, то деревья, полученные путем добавления дополнительного ребра к этим корням, одинаковые (изоморфные). Таким образом нам нужно подсчитать количество корней с различными метками. Так же нужно не забыть, что если у корня степень вершины уже 4, то новое ребро в этот корень добавит невозможно.

Описанное выше решение будет работать за 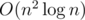, т.к. мы рассматриваем n подвешенных деревьев и в каждом дереве пробегаем по всем n вершинам, расставляя метки в map за .

Теперь поймем, как ускорить это решение до .

Заведем массив b, где b[v_i]   —  это метка, которую необходимо поставить в вершину v_i, если подвесить дерево за эту вершину. Тогда ответом на задачу будет кол-во различных чисел в массиве b.

Подвесим дерево за вершину root и подсчитаем значения a[v_i]. Тогда b[root] = a[root], а остальные значения b[v_i] можно подсчитать, проталкивая информацию сверху вниз.

Итоговая асимптотика: .

Div. 1 E — День рождения Матвея

Идея: BigBag.
Разработка: BigBag, GlebsHP.

Докажем, что расстояние между любыми двумя вершинами не превосходит MaxDist = 2·sigma - 1, где sigma  —  размер алфавита. Рассмотрим какой-нибудь кратчайший путь от позиции i до позиции j. Заметим, что в этом пути каждая буква ch будет встречаться не более двух раз (т.к. иначе можно было бы просто перепрыгнуть с первой буквы ch на последнюю и получить более короткий путь). Таким образом общее количество букв на пути не более 2·sigma, следовательно длина пути не превосходит 2·sigma - 1.

Пусть dist_i, c  —  расстояние от позиции i, до какой-нибудь позиции j, где s_j = c. Эти значения можно получить с помощью моделирования bfs для каждой различной буквы c. Моделировать bfs довольно легко можно за 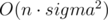(над этим рекомендуется подумать самостоятельно).

Пусть dist(i, j)  —  расстояние между позициями i и j. Поймем, как находить dist(i, j) с помощью заранее подсчитанных значений dist_i, c.

Рассмотрим два принципиальных случая:

1. Оптимальный путь проходит только через ребра первого типа (между соседними позициями в строке). В этом случае расстояние равно .
2. В оптимальном пути есть хотя бы одно ребро второго типа. Пусть это был прыжок между двумя буквами типа c. Тогда в таком случае расстояние равно dist_i, c + 1 + dist_c, j.

Суммируя эти два случая получаем, что .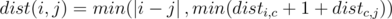

Исходя из этого, уже можно написать решение, работающее за 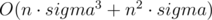. То есть можно просто перебрать все пары позиций (i, j), и для каждой пары обновить ответ расстоянием, полученным по описанной выше формуле.

Поймем, как можно ускорить это решение.

Будем перебирать только первую позицию i = 1..n. Для всех j таких, что 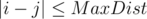, посчитаем расстояние по выше описанной формуле.

Теперь нам нужно для фиксированного i найти max(dist(i, j)) для 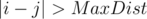. В этом случае dist(i, j) = min(dist_i, c + 1 + dist_c, j).

Для этого посчитаем еще одну вспомогательную величину dist_c1, c2  —  минимальное расстояние между позициями i и j такими, что s_i = c1 и s_j = c2. Это можно легко сделать, используя dist_i, c.

Нетрудно заметить, что dist_sj, c ≤ dist_j, c ≤ dist_sj, c + 1. То есть для каждой позиции j мы можем составить маску mask_j из sigma бит, i-й бит которой равен dist_j, c - dist_sj, c. Теперь расстояние можно однозначно определить, зная только s_j и mask_j.
То есть сейчас dist_j, c = dist_sj, c + mask_j, c.

Будем поддерживать массив cnt_c, mask  —  количество таких j, что 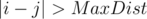, s_j = c и mask_j = mask. Теперь вместо того, чтобы для фиксированного i перебирать все возможные j, можно перебирать только пару (c, mask), и если cnt_c, mask ≠ 0, то обновлять ответ.

Итоговая асимптотика: 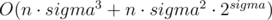.