Special thanks to Seyaua for help with translation.

Div. 2 A — Vitya in the Countryside

Idea: _XuMuk_.
Preparation: _XuMuk_.

There are four cases that should be carefully considered:

1. a_n = 15   —  the answer is always DOWN.

2. a_n = 0   —  the answer is always UP.

3. If n = 1   —  the answer is -1.

4. If n > 1, then if a_n–1 > a_n   —  answer is DOWN, else UP.

Time Complexity: .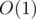

Div. 2 B — Anatoly and Cockroaches

Idea: _XuMuk_.
Preparation: _XuMuk_.

We can notice that there are only two possible final coloring of cockroaches that satisfy the problem statement: rbrbrb... or brbrbr...

Let’s go through both of these variants.

In the each case let's count the number of red and black cockroaches which are not standing in their places. Let's denote these numbers as x and y. Then it is obvious that the min(x, y) pairs of cockroaches need to be swapped and the rest should be repaint.

In other words, the result for a fixed final coloring is exactly min(x, y) + max(x, y) - min(x, y) = max(x, y). The final answer for the problem is the minimum between the answers for the first and the second colorings.

Time Complexity: .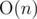

Div. 1 A — Efim and Strange Grade

Idea: BigBag.
Preparation: BigBag.

One can notice that the closer to the decimal point we round our grade the bigger grade we get. Based on this observation we can easily solve the problem with dynamic programming.

Let dp_i be the minimum time required to get a carry to the (i - 1)-th position.

Let's denote our grade as a, and let a_i be the (i)-th digit of the a. There are three cases:

1. If a_i ≥ 5, then dp_i = 1.

2. If a_i < 4, then dp_i = inf (it means, that we cann't get a carry to the (i - 1)-th position).

3. If a_i = 4, then dp_i = 1 + dp_i + 1.

After computing dp, we need to find the minimum pos such that dp_pos ≤ t. So, after that we know the position where we should round our grade.

Now we only need to carefully add 1 to the number formed by the prefix that contains pos elements of the original grade.

Time Complexity: .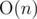

Div. 1 B — Alyona and Copiers

Idea: _XuMuk_.
Preparation: BigBag.

Deleted

div. 1 C — Sasha and Array

Idea: BigBag.
Preparation: BigBag.

Let's denote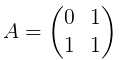

Let's recall how we can quickly find n-th Fibonacci number. To do this we need to find a matrix product .

In order to solve our problem let's create the following segments tree: in each leaf which corresponds to the element i we will store a vector 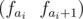and in all other nodes we will store the sums of all the vectors that correspond to a given segment.

Now, to perform the first request we should multiply all the vectors in a segment [l..r] by 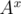and to get an answer to the second request we have to find a sum in a segment [l..r].

Time Complexity: .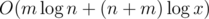

Div. 1 D — Andrew and Chemistry

Idea: _XuMuk_.
Preparation: BigBag.

Let’s first figure out how we can solve the problem in time.

Let’s pick a vertex we’re going to add an edge to and make this vertex the root of the tree. For each vertex v_i we’re going to assign a label a[v_i] (some number). The way we assign labels is the following: if the two given vertices have the same subtrees they’re going to get the same labels, but if the subtrees are different then the labels for these vertices are going to be different as well.

We can do such labeling in a following way: let’s create a map<vector<int>, int> m (the maximum degree for a vertex is 4, but let’s assume that the length of the vector is always equal to 4). Let m[{x, y, z, w}] be a label for a vertex which has children with the labels x, y, z, w. Let’s note that the vector {x, y, z, w} should be sorted to avoid duplications, also if the number of children is less than 4 then we’ll store  - 1’s for the missing children (to make the length of a vector always equal to 4). Let’s understand how we can compute the value for the label for the vertex v. Let’s recursively compute the labels for its children: v₁, v₂, v₃, v₄.
Now, if m.count({a[v1], a[v2], a[v3], a[v4]}) then we use the corresponding value. Otherwise, we use the first unused number: m[{a[v1], a[v2], a[v3], a[v4]}]=cnt++.

Now, let’s pick another vertex which we’re going to add an edge to. Again, let’s make it the root of the tree and set the labels without zeroing out our counter cnt. Now, let’s do the same operation for all the other possible roots (vertices, n times). Now, one can see that if the two roots have the same labels, then the trees which can be obtained by adding an edge to these roots, are exactly the same. Thus, we only need to count the amount of roots with different labels. Also, we should keep in mind that if a degree for a vertex is already 4 it’s impossible to add an edge to it.

The solution described above has the time complexity , because we consider n rooted trees and in the each tree we iterate through all the vertices (n), but each label update takes .

Let’s speed up this solution to .

Let b be an array where b[v_i] is a label in a vertex v_i if we make this vertex the root of the tree. Then the answer to the problem is the number of different numbers in the array b. Let’s root the tree in a vertex root and compute the values a[v_i]. Then b[root] = a[root] and all the other values for b[v_i] we can get by pushing the information from the top of the tree to the bottom.

Time complexity: .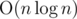

Div. 1 E — Matvey's Birthday

Idea: BigBag.
Preparation: BigBag, GlebsHP.

Let’s prove that the distance between any two vertices is no more than MaxDist = 2·sigma - 1, where sigma is the size of the alphabet. Let’s consider one of the shortest paths from the position i to the position j. One can see that in this path each letter ch occurs no more than two times (otherwise you could have skipped the third occurrence by jumping from the first occurrence to the last which gives us a shorter path). Thus, the total amount of letters in the path is no more than 2·sigma which means that the length of the path is no more than 2·sigma - 1.

Let dist_i, c be the distance from the position i to some position j where s_j = c. These numbers can be obtained from simulating bfs for each letter c. We can simulate bfs in O(n·sigma²) (let’s leave this as an exercise to the reader).

Let dist(i, j) be the distance between positions i and j. Let’s figure out how we can find dist(i, j) using precomputed values dist_i, c.

There are two different cases:

1. The optimal path goes through the edges of the first type only. In this case the distance is equal to .

2. The optimal path has at least one edge of the second type. We can assume that it was a jump between two letters c. Then, in this case the distance is dist_i, c + 1 + dist_c, j.

Adding these two cases up we get: .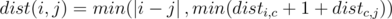

Let’s iterate over the possible values for the first position i = 1..n. Let’s compute the distance for all such j, where 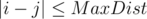by the above formula.

Now, for a given i we have to find max(dist(i, j)) for 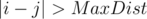. In this case dist(i, j) = min(dist_i, c + 1 + dist_c, j).

Let’s compute one additional number dist_c1, c2  —  the minimal distance between positions i and j where s_i = c₁ and s_j = c₂. This can be easily done using dist_i, c.

One can notice that dist_sj, c ≤ dist_j, c ≤ dist_sj, c + 1. It means that for every position j we can compute a mask mask_j with sigma bits where i-th bit is equal to dist_j, c - dist_sj, c. Thus, we can compute the distance using only s_j and mask_j.
I.e. now dist_j, c = dist_sj, c + mask_j, c.

Let cnt be an array where cnt_c, mask is the number of such j where 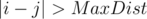, s_j = c and mask_j = mask. Now, instead of iterating over j for a given i we can iterate over (c, mask) and if cnt_c, mask ≠ 0 we’ll be updating the answer.

Time complexity: 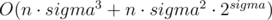.