Thanks to the $$$20$$$+ teams who participated in the TJIOI 2024 contest in-person and others who competed virtually in the mirror. We hope you enjoyed the problems! Please let us know in the comments if you have any questions or feedback.
[problem:523552A]
Idea: DanielQiu, Preparation: DanielQiu
Rewrite $$$c$$$ in its binary representation. Let's call $$$c$$$ good if it has an even number of trailing zeros, possibly none.
Claim: Assume $$$c > 1$$$. If $$$c$$$ is good, then the current player can always make $$$c$$$ not good after their turn. On the flip side, if $$$c$$$ is not good, no matter what the current player does, it will always be good after their turn.
Proof: For the first part, if $$$c$$$ has $$$2$$$ or more trailing zeros, we can divide by $$$2$$$ to leave an odd number of trailing zeros. If $$$c$$$ doesn't have trailing zeros, we can subtract $$$1$$$ to leave exactly one trailing zero. In both of these cases, $$$c$$$ is not good after the turn. For the second part, if $$$c$$$ has an odd number of trailing zeros, dividing by $$$2$$$ will leave an even number of trailing zeros. Subtracting $$$1$$$ will make the last digit of $$$c$$$ equal to $$$1$$$, which means $$$c$$$ is good.
Thus, if $$$c$$$ is good for the current player, then with the correct move, it is certain that $$$c$$$ will be good on their next turn. Since $$$c$$$ must eventually equal $$$1$$$, and $$$1$$$ is good, this means that if $$$c$$$ is good for the current player, they can ensure that $$$c$$$ will be $$$1$$$ on their turn, meaning that they eat the last cookie and win the game. So if $$$c$$$ is good initially, then Cookie Monster wins, otherwise Elmo wins.
#include <bits/stdc++.h>
using namespace std;
#define ll long long
signed main() {
ios::sync_with_stdio(false);
cin.tie(0);
ll x;
cin >> x;
if (x % 2 == 1) {
cout << "Cookie Monster" << endl;
} else {
int cnt = 0;
while(x % 2 == 0 && x) {
x /= 2;
cnt++;
}
if (cnt % 2 == 0) {
cout << "Cookie Monster" << endl;
} else {
cout << "Elmo" << endl;
}
}
}
[problem:523552B]
Together, Cookies Monster and Elmo remove $$$n+m$$$ cookies in their turns. They will keep doing this until the number of cookies and left is less than $$$n+m$$$. If the number of cookies left is $$$0$$$, that means Elmo took the last cookie and there are none left. Otherwise, if the number of cookies left is less than or equal to $$$n$$$, Cookie Monster can remove all the remaining cookies. If this is not the case, Elmo wins.
#include <bits/stdc++.h>
using namespace std;
int main() {
int n, m, c; cin >> n >> m >> c;
c--;
c %= n + m;
if (c < n) cout << "Cookie Monster" << endl;
else cout << "Elmo" << endl;
}
[problem:523552C]
Idea: ChiMasterBing, Preparation: ChiMasterBing
Let's visualize this problem as a bar graph, where the $$$x$$$ axis represents each friend, and the $$$y$$$ axis represents the amount of cookies each friend has initially.
In terms of the bar graph, an operation of $$$[L, R]$$$ would be adding a row of cookies at the top from $$$L$$$ to $$$R$$$, and letting that row to "fall" until each of the stacks in $$$[L, R]$$$ are increased by one. However, we can observe that we don't actually have to let the row fall. That is, we can represent each operation as just a stationary $$$1$$$ by $$$(R-L+1)$$$ rectangle in the grid.
It is easy to see that we will need at least $$$T = max(arr)$$$ time no matter what $$$M$$$ we're given. So, let's consider the max amount of additional cookies we can handle if we're only allocated $$$max(arr)$$$ time. Here, we can do at most $$$T$$$ operations (add $$$T$$$ rectangles) as each operation takes $$$1$$$ second. Additionally, all rectangles have to be placed below height $$$T$$$. The problem then becomes how to add the maximum amount of 1-high rectangles into the bar graph that the total area of the rows we added is maximum.
It is obvious that we want to draw rectangles to the maximum width we can without overlapping with bars. This leads to the following important observation about the rectangles. Suppose a rectangle has a $$$y$$$ value less than another rectangle and that the lower rectangle overlaps in $$$x$$$ with the higher rectangle. The lower rectangle is guaranteed to have $$$x$$$ values completely contained/under the higher rectangle, implying that it's width is also less than or equal to the top rectangle. This means that we can apply a greedy argument. We want to greedily place the largest width rectangles which start at the top, and all next-biggest rectangles will already be under some rectangle that we already placed. One way we can simulate this is to use a priority queue of rectangles, which takes $$$O(n \log n)$$$. Each time we place a rectangle, we add the adjacent rectangles underneath. These rectangles are found with a segment tree; repeatedly query for bars with height one below the placed bar.
From this process, we have found the greatest $$$M$$$ that can be handled if $$$T = max(arr)$$$. What if $$$T = max(arr)+1$$$. Well, we get 1 extra operation compared to when we had $$$T = max(arr)$$$. It happens conveniently that in the bar graph, the maximum height at which we can place rectangles is increased by 1 too! That means we can greedily place 1 rectangle that fills that entire row, and we can be confident that nothing is better than that. This argument can be used inductively for $$$T+2, T+3, ...$$$.
In this way, we have found a general formula for the maximum $$$M$$$ for each $$$T$$$: $$$M = [M @ T = max(arr)] + (T-max(arr)) * N$$$. It is easy to see how this can be used to solve queries in $$$O(1)$$$.
#include <bits/stdc++.h>
using namespace std;
#define int long long
template<class T> struct SimpleSegmentTree {
int len;
vector<T> segtree;
T DEFAULT = {-1, -1};
SimpleSegmentTree(int _len) : len(_len), segtree(_len * 2, DEFAULT) {}
void set(int ind, T val) {
ind += len; segtree[ind] = val;
for (; ind > 1; ind /= 2) segtree[ind / 2] = merge(segtree[ind], segtree[ind ^ 1]);
}
T query(int start, int end) {
T res = DEFAULT;
for (start += len, end += len; start < end; start /= 2, end /= 2) {
if (start % 2 == 1) { res = merge(res, segtree[start++]); }
if (end % 2 == 1) { res = merge(res, segtree[--end]); }
}
return res;
}
T merge(T a, T b) {
if (a.first > b.first) return a;
else if (a.first == b.first) {
if (a.second < b.second) return a;
}
return b;
}
};
using SegTree = SimpleSegmentTree<pair<int, int>>; // (value, index)
struct block {
int L, R, H, LEN;
};
struct compare {
bool operator()(block const& a, block const& b) {
return a.LEN < b.LEN;
}
};
SegTree tree(0); //tree keeps track of highest nodes online. Used to get next "blocks" in O(log(N))
priority_queue<block, vector<block>, compare> pq; // (length, [L, R])
int N, Q;
void populate(block b) { //push adjacent blocks into PQ
int nxtL = b.L;
while (true) {
pair<int, int> p = tree.query(b.L, b.R + 1); //p is biggest, leftmost
if (p.first != b.H-1) break;
block nxt; nxt.L = nxtL; nxt.R = p.second-1; nxt.H = b.H-1; nxt.LEN = nxt.R-nxt.L+1;
nxtL = p.second + 1;
tree.set(p.second, {-1, -1});
if (nxt.LEN > 0) pq.push(nxt);
}
block nxt; nxt.L = nxtL; nxt.R = b.R; nxt.H = b.H-1; nxt.LEN = nxt.R-nxt.L+1;
if (nxt.LEN > 0) pq.push(nxt);
}
signed main() {
ios_base::sync_with_stdio(false); cin.tie(NULL);
cin>>N>>Q;
tree.segtree.resize(2 * N, {-1, -1});
tree.len = N;
for (int i=0; i<N; i++) {
int a; cin>>a; tree.set(i, {a, i});
}
int base = 0, T = tree.query(0, N).first;
block b; b.L = 0; b.R = N-1; b.LEN = b.R-b.L+1; b.H = T+1;
populate(b);
for (int i=0; i<T; i++) { //you can take T operations at most
if (pq.empty()) break;
block b = pq.top(); pq.pop();
base += b.LEN;
populate(b);
}
int zero = 0;
while (Q--) { //for more time, greedily take more blocks on top
int M; cin>>M;
M = max(zero, M-base);
int ans = T;
ans += (M / N);
M -= (M / N) * N;
if (M > 0) ans++;
cout<<ans<<"\n";
}
}
[problem:523552D]
Idea: avnithv, Preparation: avnithv
The solution exists if and only if $$$n \equiv 0 \pmod 4$$$ or $$$n \equiv 1 \pmod 4$$$. We can prove that it impossible to find a solution if $$$n \equiv 2 \pmod 4$$$ or $$$n \equiv 3 \pmod 4$$$. (Hint: Consider the parity of the sum of the number of chips on all the uneaten cookies and how this changes after each day. This sum should equal $$$0$$$ at the end.)
Let's first see how to construct it for the case $$$n \equiv 0 \pmod 4$$$. There are probably many ways to construct a solution, some of them are probably simpler, but this is our solution.
We will use each of the first $$$n$$$ numbers in a different operation. So now the problem can be thought of as choosing pairs of the last $$$2n$$$ numbers whose differences map to the numbers from $$$1$$$ to $$$n$$$.
Consider the even differences for now, the numbers $$$2$$$, $$$4$$$, ... $$$n-2$$$, $$$n$$$. We can cover all of these with pairs $$$(2n, 3n)$$$, $$$(2n+1, 3n-1)$$$, ..., $$$(\frac{5n}{2}-1, \frac{5n}{2}+1)$$$. This uses up the values from $$$2n$$$ to $$$3n$$$ inclusive with the singular exception of $$$\frac{5n}{2}$$$. We will let this be the larger value in the pair with the difference $$$n-1$$$. The smaller value in that pair will be $$$\frac{3n}{2}+1$$$.
Now we have the numbers from $$$n+1$$$ to $$$\frac{3n}{2}$$$ inclusive and $$$\frac{3n}{2}+2$$$ to $$$2n-1$$$ inclusive remaining, and can use the odd-numbered pairs from $$$1$$$ to $$$n-3$$$, inclusive.
We use the $$$\frac{n}{2}-1$$$ pair to cover $$$\frac{3n}{2}$$$ and $$$2n-1$$$. Now, the pairs that are greater than $$$\frac{n}{2}-1$$$ can fit in $$$(n+1, 2n-2)$$$, $$$(n+2, 2n-3)$$$, ... $$$(\frac{5n}{4}-1, \frac{7n}{4})$$$. All of the pairs that are less than $$$\frac{n}{2}-1$$$, excluding $$$1$$$ for the moment, can fit in $$$(\frac{5n}{4}+2, \frac{7n}{4}-1)$$$, $$$(\frac{5n}{4}+3, \frac{7n}{4}-2)$$$, ... $$$(\frac{3n}{2}-1, \frac{3n}{2}+2)$$$. And finally, the $$$1$$$ fits perfectly in the remaining gap of $$$(\frac{5n}{4}, \frac{5n}{4}+1)$$$.
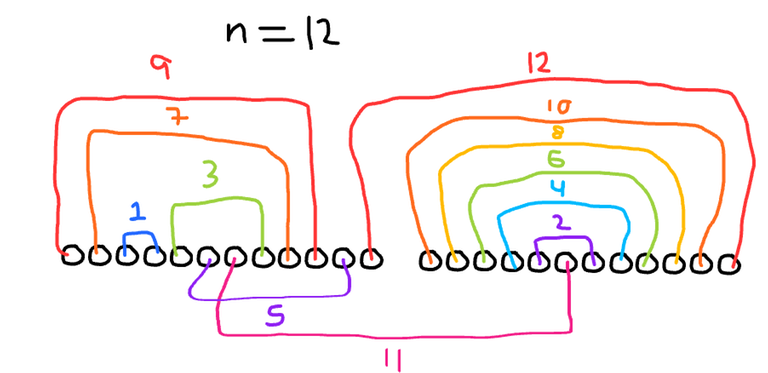
The construction for the second case with $$$n \equiv 1 \pmod 4$$$ is similar, but some of the details are slightly different.
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
void solve() {
int n; cin >> n;
if (n % 4 == 2 || n % 4 == 3) {
cout << "No" << endl;
return;
}
cout << "Yes" << endl;
if (n == 1) {
cout << "1 2 3" << endl;
} else if (n == 4) {
cout << "1 5 6" << endl;
cout << "2 8 10" << endl;
cout << "3 9 12" << endl;
cout << "4 7 11" << endl;
} else if (n == 5) {
cout << "1 5 6" << endl;
cout << "2 10 12" << endl;
cout << "3 11 14" << endl;
cout << "4 9 13" << endl;
cout << "7 8 15" << endl;
} else if (n % 4 == 0) {
int l = 2*n, r = 3*n;
while (l != r) {
cout << r - l << " " << l << " " << r << endl;
l++; r--;
}
cout << n - 1 << " " << 3 * n / 2 + 1 << " " << 5 * n / 2 << endl;
cout << n / 2 - 1 << " " << 3 * n / 2 << " " << 2 * n - 1 << endl;
l = n + 1; r = 2 * n - 2;
while (r - l > n / 2 - 1) {
cout << r - l << " " << l << " " << r << endl;
l++; r--;
}
l = 3 * n / 2 - 1; r = 3 * n / 2 + 2;
while (r - l < n / 2 - 1) {
cout << r - l << " " << l << " " << r << endl;
l--; r++;
}
cout << 1 << " " << 5 * n / 4 << " " << 5 * n / 4 + 1 << endl;
} else {
int l = 2 * n + 1, r = 3 * n;
while (l != r) {
cout << r - l << " " << l << " " << r << endl;
l++; r--;
}
cout << n << " " << 3 * n / 2 + 1 << " " << 5 * n / 2 + 1 << endl;
cout << n / 2 - 1 << " " << 3 * n / 2 + 2 << " " << 2 * n << endl;
l = n + 1; r = 2 * n - 1;
while (r - l > n / 2 - 1) {
cout << r - l << " " << l << " " << r << endl;
l++; r--;
}
l = 3 * n / 2; r = 3 * n / 2 + 3;
while (r - l < n / 2 - 1) {
cout << r - l << " " << l << " " << r << endl;
l--; r++;
}
cout << 1 << " " << 5 * n / 4 + 1 << " " << 5 * n / 4 + 2 << endl;
}
}
int main() {
int t; cin >> t;
while (t--) solve();
}
[problem:523552E]
Idea: avnithv, Preparation: avnithv
In this problem, you just have to consider several cases. We orient both the original and cut pieces of cake so that it shares the bottom left corner. There are two ways the piece cake can be oriented, either with the side of length $$$a$$$ vertical or horizontal. Additionally, the first cut that we make can either be horizontal or vertical. Thus, there are $$$4$$$ main cases to consider. Make sure to check that a given orientation is possible (i.e. the cut piece of cake lies completely inside the original one). Also, carefully handle the cases when the original and cut pieces of cake have the same side length or are equal, in which case you may only need to make $$$1$$$ or $$$0$$$ cuts.
#include <bits/stdc++.h>
using namespace std;
int main() {
int x, y, a, b; cin >> x >> y >> a >> b;
int ans = 2000000000;
if (a == x && b == y || a == y && b == x) ans = 0;
if (a <= x && b <= y) {
ans = min(ans, x + (a == x ? 0 : b));
ans = min(ans, y + (b == y ? 0 : a));
}
if (a <= y && b <= x) {
ans = min(ans, x + (b == x ? 0 : a));
ans = min(ans, y + (a == y ? 0 : b));
}
if (ans == 2000000000) ans = -1;
cout << ans << endl;
}
[problem:523552F]
Idea: avnithv, Preparation: avnithv
We can solve this problem with Dynamic Programming.
Let $$$dp[i][j][k]$$$ represent the maximum width of a rectangular piece of cake that you can place so that the right edge of the cake lies on column $$$i$$$ and goes from rows $$$j$$$ to $$$k$$$. From the constraints, we can infer that $$$n \leq 500$$$, so this will not use up too much time or memory.
To calculate $$$dp$$$, we can move across columns from left to right. If the current cake is unfilled for every location along column $$$i$$$ between rows $$$j$$$ and $$$k$$$, we can update $$$dp[i][j][k] = dp[i-1][j][k] + 1$$$. Otherwise, it is impossible to place a piece of cake there and $$$dp[i][j][k] = 0$$$. We can quickly check this using a 2D prefix sum array.
Note that if a piece with width $$$m$$$ can be placed with its right edge at a certain $$$dp$$$ state, then so can a piece of length $$$m-1$$$. For each fixed height ($$$k-j$$$), we can store the $$$dp$$$ values in an array and take the suffix sum, accounting for the previous fact. This allows us to precompute the answers to all queries.
#include <bits/stdc++.h>
#define int long long
using namespace std;
signed main() {
int n, m, q; cin >> n >> m >> q;
bool grid[n][m];
for (int i = 0; i < n; i++) {
string s; cin >> s;
for (int j = 0; j < m; j++) grid[i][j] = (s[j] == '1');
}
int pref[n+1][m+1];
memset(pref, 0, sizeof(pref));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
pref[i][j] += (int)grid[i-1][j-1] + pref[i-1][j] + pref[i][j-1] - pref[i-1][j-1];
}
}
// maximum width of subgrid with right column $$$i$$$ and height from rows $$$j$$$ to $$$k$$$.
int dp[m][n][n];
int pos[n][m];
memset(dp, 0, sizeof(dp));
memset(pos, 0, sizeof(pos));
for (int j = 0; j < n; j++) {
for (int k = j; k < n; k++) {
if (pref[k+1][1] - pref[k+1][0] - pref[j][1] + pref[j][0] == 0) {
dp[0][j][k] = 1;
pos[k-j][0]++;
}
}
}
for (int i = 1; i < m; i++) {
for (int j = 0; j < n; j++) {
for (int k = j; k < n; k++) {
if (pref[k+1][i+1] - pref[k+1][i] - pref[j][i+1] + pref[j][i] == 0) {
dp[i][j][k] = dp[i-1][j][k]+1;
pos[k-j][dp[i][j][k]-1]++;
} else dp[i][j][k] = 0;
}
}
}
for (int i = 0; i < n; i++) {
for (int j = m-2; j >= 0; j--) {
pos[i][j] += pos[i][j+1];
}
}
while (q--) {
int h, w; cin >> h >> w;
h--; w--;
cout << pos[h][w] << endl;
}
}
[problem:523552G]
The number of good snacks is only limited by $$$a$$$ and $$$b$$$ since $$$c$$$ can be disregarded since all those cookies were stolen. The number of good snacks is simply which type of cookie has a smaller number of servings and will run out first.
#include <bits/stdc++.h>
using namespace std;
int main() {
int x, y, z;
cin >> x >> y >> z;
cout << min(x, y) << endl;
}
[problem:523552H]
Idea: DanielQiu, Preparation: DanielQiu
We can keep track of the number of occurrences of each letter in $$$A$$$. Then we can keep track of the number of occurrences of each letter in $$$B$$$. Since we can rearrange A however we like, we can rearrange $$$A$$$ such that we form the string $$$B$$$ as much as possible as a prefix. To find out the maximum number of copies of $$$B$$$ each letter can form, we should divide the occurrences of each letter in $$$A$$$ by the occurrences of each letter in $$$B$$$, discarding any remainders. The answer is the minimum value of these quotients.
#include <bits/stdc++.h>
#define int long long
using namespace std;
signed main(){
string a, b;
cin>>a>>b;
int cnta[26];
int cntb[26];
memset(cnta, 0, sizeof(cnta));
memset(cntb, 0, sizeof(cntb));
for(char c: a){
cnta[c-'a']++;
}
for(char c: b){
cntb[c-'a']++;
}
int ret = INT_MAX;
for(int i=0; i<26; i++){
if(cntb[i]>0){
ret = min(ret, cnta[i]/cntb[i]);
}
}
cout<<ret<<endl;
}
[problem:523552I]
An arithmetic sequence can be formed between numbers only if they all have the same common remainder when divided by $$$d$$$. After separating the values of the array based on their modulus $$$d$$$, for each modulus, we sort the array. Then, we can start off with an empty arithmetic sequence and loop through the array, checking if adding the current element to the end of the arithmetic sequence and possibly removing the first element will create a new arithmetic sequence of length $$$m$$$ that will increase our answer by $$$1$$$.
#include <bits/stdc++.h>
using namespace std;
int main() {
int n, d, m; cin >> n >> d >> m;
vector<int> arr(n);
for (int i = 0; i < n; i++) cin >> arr[i];
map<int, vector<int>> mp;
for (int i = 0; i < n; i++) {
int rem = arr[i] % d;
int b = (arr[i]-rem)/d;
if (!mp.count(rem)) mp[rem] = vector<int>();
mp[rem].push_back(b);
}
int ans = 0;
for (auto x : mp) {
vector<int> v = x.second;
sort(v.begin(), v.end());
v.erase(unique(v.begin(), v.end()), v.end());
int l = v.size();
for (int i = l-1; i >= 0; i--) {
if (l - i == m) {
l--;
ans++;
}
if (i > 0 && v[i-1]+1 < v[i]) l=i;
}
}
cout << ans << endl;
}
[problem:523552J]
To ensure we decrease the monsters health by $$$1$$$, we can either upgrade the tower it is currently at or perform the optimal combination of upgrades for all the node's children, since we don't know which child it will go to. If the current node is a leaf, then the optimal combination is just upgrading the current node. To compute the answer, we can run a depth first search where we calculate the minimum cost to decrease the monster's health by $$$1$$$ by calculating the minimum cost for each node of the tree by comparing it with the sum of the minimum costs for each its children, rooting the tree at node $$$1$$$.
#include <bits/stdc++.h>
using namespace std;
const int mn=2e5;
vector<int> adj[mn];
bool visited[mn]={0};
int cost[mn];
int dfs(int node) {
visited[node]=true;
long long subtree_sum=0;
for(int u:adj[node]) {
if(!visited[u]) {
subtree_sum+=dfs(u);
}
}
if(subtree_sum==0) return cost[node];
return min((long long)cost[node], subtree_sum);
}
int main() {
int n, h; cin >> n >> h;
for(int i=0; i<n; i++) cin >> cost[i];
for(int i=0; i<n-1; i++) {
int u, v; cin >> u >> v;
u--, v--;
adj[u].push_back(v);
adj[v].push_back(u);
}
cout << (long long)dfs(0)*h;
}
[problem:523552K]
Idea: avnithv, Preparation: avnithv
Notice that since the original deck is sorted, each of the stacks will be in decreasing order from top to bottom. When we stack the stacks on top of each other, each stack will still be in decreasing order. Thus, whenever we see two adjacent cookies $$$a_i$$$ and $$$a_{i+1}$$$ in increasing order ($$$a_i < a_i+1$$$) this must mean that $$$a_i$$$ and $$$a_{i+1}$$$ were part of different stacks. So we can loop through the array and count the number of adjacent cookies that are in increasing order, adding $$$1$$$ to get our answer.
#include <bits/stdc++.h>
using namespace std;
int main() {
int t; cin >> t;
while (t--) {
int n; cin >> n;
vector<int> arr(n);
for (int i = 0; i < n; i++) cin >> arr[i];
int ans=1;
for (int i = 0; i < n-1; i++) {
if (arr[i] < arr[i+1]) ans++;
}
cout << ans << endl;
}
}
[problem:523552L]
Idea: MunirKP, Preparation: MunirKP
The number of points on either side of the line is invariant. For the provided input, there is $$$1$$$ point to the left of the line.
Call the convex hull of all the points the \textit{outer hull}, and the convex hull of the remaining points the \textit{inner hull}. The outer and inner hull can be computed in $$$O(N)$$$ with Andrew's algorithm. To maintain the invariant, the line must always cross the outer hull but never cross the inner hull.
At some moment, call the current pivot $$$P$$$. The new pivot must be one of three points:
- The lone ``invariant'' point $$$Q$$$
- The point $$$R$$$ on the outer hull with minimum $$$∠QPR$$$
- The point $$$S$$$ on the inner hull with minimum $$$∠QPS$$$
$$${Q, R, S}$$$ can be maintained by two pointers which are incrementally updated. The line switches pivots $$$O(N)$$$ times before returning to the initial state. Total complexity is therefore $$$O(N)$$$.
Visuals:
- https://www.youtube.com/watch?v=M64HUIJFTZM
- https://www.desmos.com/calculator/eec1g1zfh9
- https://www.desmos.com/calculator/kylvoqkmcs
Bonus:
- Solve the general case! (pivot is any point to begin)
- Generate test data! Specifically, generate a set of points in ``seemingly'' uniformly random manner so that no three points are collinear
from functools import cmp_to_key
def cross(p, q, r):
v = (r[0]-p[0], r[1]-p[1])
w = (q[0]-p[0], q[1]-p[1])
return (v[1]*w[0] - v[0]*w[1])
def convex_hull(pnts):
lv, li = min((v,i) for i,v in enumerate(pnts))
cnds = sorted({*pnts}-{lv}, key=cmp_to_key(lambda a, b : cross(lv, a, b)))
hull = [lv]
for pt in cnds:
while len(hull) > 1 and cross(hull[-2], hull[-1], pt) >= 0:
hull.pop()
hull.append(pt)
return hull
def main():
N = int(input())
pnts = [tuple(map(int, input().split())) for i in range(N)]
oh = convex_hull(pnts)
if len(oh) == len(pnts):
print(len(oh))
if pnts[1]==oh[-1]:
print('\n'.join(f"{p[0]} {p[1]}" for p in [oh[-1],oh[1],oh[0]]+oh[2:-1]))
else:
print('\n'.join(f"{p[0]} {p[1]}" for p in [oh[1],oh[0]]+oh[2:]))
return
ih = convex_hull([*{*pnts} - {*oh}])
pivs = [pnts[1]]
ii = 0
st = 0
if pnts[1]==oh[1] and oh[1][1] > oh[0][1]:
pivs.append(oh[0])
st = 1
for oi in [*range(st,len(oh))]+[0]:
if len(ih)==2:
if cross(oh[oi], ih[ii], ih[(ii+1)%len(ih)]) > 0: ii = (ii+1)%len(ih)
elif len(ih)>2:
while cross(oh[oi], ih[ii], ih[(ii+1)%len(ih)]) > 0: ii = (ii+1)%len(ih)
while cross(pivs[-1], ih[ii], oh[(oi+1)%len(oh)]) < 0:
pivs.append(ih[ii])
ii = (ii+1)%len(ih)
pivs.append(oh[(oi+1)%len(oh)])
pivs.append(oh[oi])
oi = (oi+1)%len(oh)
vis = {pt:len(pivs)-i-1 for i,pt in enumerate(pivs[::-1])}
print(len(vis))
print('\n'.join(f"{pt[0]} {pt[1]}" for i,pt in enumerate(pivs) if vis[pt]==i))
if __name__=='__main__': main()
[problem:523552M]
Idea: flight, Preparation: flight
The following solutions consider the graph theoretic interpretation of finding the number of permutation graphs of size $$$n$$$ such that all cycles have a length that is a multiple of $$$k.$$$
Solution 1
There are two components to this problem. The first component is deciding which labels go to which cycles (and deciding the cycle sizes themselves), and the second component is deciding how to order labels within their own cycles.
The second component is obvious: given $$$n$$$ labels, it is known that there are $$$(n-1)!$$$ ways to order them into a cycle. This is because there are $$$n!$$$ ways to order them in a line, and $$$n$$$ repetitions due to cyclic shifting.
The first component, however, is more difficult. We now turn to the use of generating functions.
Consider the generating function $$$f(x) = \frac{x^k}{k!} * (k-1)! + \frac{x^{2k}}{(2k)!} * (2k-1)! + \dots.$$$ This is the exponential generating function of the cycle reordering we are allowed to perform. More specifically, given we want to add a cycle of length $$$m$$$ to the graph, the coefficient $$$\left[\frac{x^m}{m!}\right] f(x)$$$ gives us the number of ways to orient the labels within the cycle.
The nice thing about exponential generating functions is that upon exponentiation, they automatically perform partitioning of labels into the corresponding sets, while simultaneously reordering them. This is shown by the fact that
where $$$B = B_0 + \frac{B_1}{1!}x + \frac{B_2}{2!}x^2 + \dots.$$$ This is essentially doing the partitioning and the reordering at the same time.
Now, consider the generating function $$$e^{f(x)} = 1 + \frac{f(x)}{1!} + \frac{f(x)^2}{2!} + \dots.$$$ This gets rid of the labeling that we assign to each "container" when we do the partioning, and represents the exponential generating function of the total number of graphs that have cycles of length all multiples of k.
Notice that $$$f(x) = \frac{x^k}{k} + \frac{x^{2k}}{2k} + \dots = \frac{1}{k}\log{\left(\frac{1}{1-x^k}\right)},$$$ due to the Taylor Series. All that remains is computing the coefficient of $$$x^n$$$ in $$$e^{f(x)} = \left(\frac{1}{1-x^k}\right)^{\frac{1}{k}}.$$$ This can be done easily using the extended binomial theorem, obtaining a closed form as shown in the code of the solution.
Solution 2
Start from the 1st node, and randomly choose $$$a_1,$$$ the node that $$$a_1$$$ points to. Likewise, choose the node that $$$a_{a_1}$$$ points to and so on until you choose $$$k$$$ nodes. Now, you have the option of either closing the cycle or continuing on, meaning that any valid node to walk to is fine. This holds true when we have visited any multiple of $$$k$$$ number of nodes.
Note that when we have visited a number of nodes, $$$x$$$, that is not a multiple of $$$k, $$$ the probability that we don't accidentally close a cycle is $$$\frac{n - x}{n - x + 1}, $$$ as there are $$$n - x + 1$$$ nodes that don't have a node pointing to it, and all nodes are valid to visit except for the node that closes the current cycle.
Therefore, we can compute the total probability of a random walk giving a correct permutation graph as $$$\prod_{x = 1, x \not\equiv 0 \pmod{k}}^{n-1} \frac{n-x}{n-x+1}.$$$ All that remains is to multiply by $$$n!,$$$ giving us our final answer.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define int ll
const int MOD = 1e9+7;
template<const int MOD> struct Modular {
static const int mod = MOD;
int v; explicit operator int() const { return v; }
Modular():v(0) {}
Modular(ll _v) { v = int((-MOD < _v && _v < MOD) ? _v : _v % MOD); if (v < 0) v += MOD; }
friend Modular mpw(Modular a, ll p) {
Modular ans = 1;
for (; p; p /= 2, a *= a) if (p&1) ans *= a;
return ans; }
friend Modular inv(const Modular& a) { return mpw(a,MOD-2);}
friend bool operator!=(const Modular& a, const Modular& b) { return !(a == b); }
friend bool operator<(const Modular& a, const Modular& b) { return a.v < b.v; }
Modular& operator+=(const Modular& o) { if ((v += o.v) >= MOD) v -= MOD; return *this; }
Modular& operator-=(const Modular& o) { if ((v -= o.v) < 0) v += MOD; return *this; }
Modular& operator*=(const Modular& o) { v = int((ll)v*o.v%MOD); return *this; }
Modular& operator/=(const Modular& o) { return (*this) *= inv(o); }
Modular operator-() const { return Modular(-v); }
Modular& operator++() { return *this += 1; }
Modular& operator--() { return *this -= 1; }
friend Modular operator+(Modular a, const Modular& b) { return a += b; }
friend Modular operator-(Modular a, const Modular& b) { return a -= b; }
friend Modular operator*(Modular a, const Modular& b) { return a *= b; }
friend Modular operator/(Modular a, const Modular& b) { return a /= b; }
friend istream& operator>>(istream& inp, Modular& a) { ll x; inp >> x; a = Modular(x); return inp;}
friend ostream& operator<<(ostream& out, const Modular& a) { out << a.v; return out; }
};
using Mint = Modular<MOD>;
using Mint = Modular<MOD>;
const int mxN = 1e6 + 10;
vector<Mint> f(mxN), invf(mxN);
Mint modpow(Mint x, int e) {
Mint base = x, curr = 1;
while (e) {
if (e & 1) {
curr *= base;
}
base = base * base;
e >>= 1;
}
return curr;
}
void precompute_factorials() {
f[0] = 1;
for (int i = 1; i < mxN; i++) {
f[i] = f[i-1] * i;
}
invf[mxN - 1] = modpow(f.back(), MOD - 2);
for (int i = mxN - 2; i >= 0; i--) {
invf[i] = invf[i+1] * (i + 1);
}
}
Mint nCr(int n, int r) {
return f[n] * invf[n-r] * invf[r];
}
int32_t main(){
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
precompute_factorials();
int n, k; cin >> n >> k;
if (n % k != 0) {
cout << 0 << "\n";
return 0;
}
int r = n / k;
Mint prod = (f[n] * invf[r]) / modpow(k, r);
for (int i = 1; i < r; i++){
prod *= (i * k + 1);
}
cout << prod << "\n";
}









