Origin URL (for Chinese): https://blog.csdn.net/can919/article/details/81840870

Translate by Baidu:

Subject matter

A tree with n nodes has two weights a and B on each edge. It takes time ai*t + b to pass through the first edge on day t. Given m, the longest path length can be obtained when t = 0, 1, 2... m-1.

An explanation

Briefly introduce Centroid decomposition on edges

Similar to Centroid decomposition on points, while dividing and conquering to select an edge, the tree is divided into two sides, so that the points on both sides are the closest.

However, edge partition and conquering of ordinary trees is easy to degenerate. The following graph will degenerate to O (n) (the official solution called it star tree)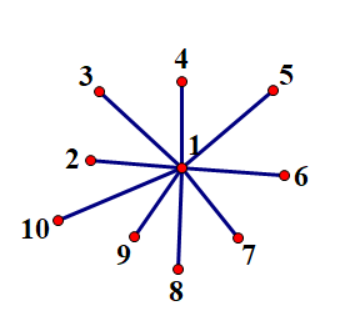

So using edge divide and conquer, we need to transform the general tree into a binary tree, so the edge divide and conquer is divided into two pieces, which ensures that the number of nodes between the two pieces must be between [n/3, n/2].

The advantage of Centroid decomposition on edges over Centroid decomposition on points is that it only divides the tree into two pieces, which in some cases reduces the amount of code needed to merge the results.

How to Centroid decomposition on edges in this problem

For this problem, we must ensure that the distance between any two points remains unchanged. When turning a binary tree, we need to create a new node, as follows: 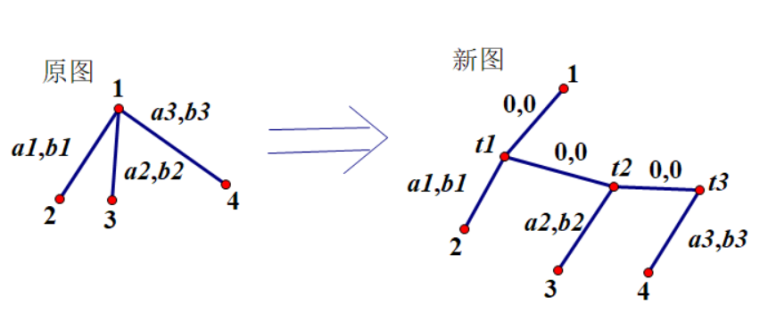For the number of edge divide and conquer trees, calculate the size of each subtree siz [u], find the largest subtree and size less than half of the total size, select this node and its father node edge as the center of gravity edge, divided into two trees.

For the two trees

It is easy to know that the longest path must be from the root to the leaf node path, statistics of all paths, the value of a and B added up separately, get the function of this path a*t + b.

These two trees, we can get a bunch of paths function, merge two paths that add their a value and b value respectively, now consider how O (n) O (n) merge all paths.

Set ai<aj

ai*t+bi<aj*t+bj

−(bj−bi)<(aj−ai)t

(bj−bi)/(aj−ai)>−t

For each function at + B at + b, consider it as a point (a, b) (a, b), maintain the convex hull according to the slope formula, and decrease the slope (do not understand the visible slope optimization)

All the path functions of the two trees are divided into two convex hull respectively.

When merging, two variables x, y are used to represent the number of nodes currently merged into the two convex hulls. Each time the slope of X and x+1 : k1, y and y+1 : K2 are judged, the larger slope + 1 is selected, and then the new x node and Y node are merged (the merging of the larger slope ensures the smaller slope change in the new convex hull, so that the convex hull can be made. Middle nodes are not missed.)

After doing edge divide and conquer, we get the convex hull of all useful paths of the whole tree, which has guaranteed the monotony of the answer and can be calculated directly.

Code:

#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
const int MAXN=200005,MAXM=MAXN*3;

struct Edge
{
    int v,a,b,id;
    Edge()=default;
    Edge(int _v,int _a,int _b,int _id):v(_v),a(_a),b(_b),id(_id) {}
};

class Tree
{
public:
    int n;
    vector<Edge> adj[MAXN*2];

    vector<Edge> &operator [] (unsigned int i)
    {
        return adj[i];
    }
    void AddEdge(int u,int v,int a,int b,int i)
    {
        adj[u].emplace_back(v,a,b,i);
        adj[v].emplace_back(u,a,b,i);
    }
};

struct Path
{
    long long a,b;
    Path()=default;
    Path(long long _a,long long _b):a(_a),b(_b) {}
    bool operator < (const Path &t)const
    {
        return a<t.a||(a==t.a&&b<t.b);
    }
};

int N,M,edgeid;
Tree F,G;

void ToBinaryTree(int u,int fa=0)
{
    int last=u;
    for(const auto &e:F[u])
        if(e.v!=fa)
        {
            G.AddEdge(last,++G.n,0,0,++edgeid);//fprintf(stderr,"[%d->%d: 0,0]\n",last,G.n);
            G.AddEdge(G.n,e.v,e.a,e.b,++edgeid);//fprintf(stderr,"[%d->%d: %d,%d]\n",G.n,e.v,e.a,e.b);
            last=G.n;
            ToBinaryTree(e.v,u);
        }
}

bool disable[MAXM];
int siz[MAXN];
Edge E[MAXN];
void GetSize(int u,int fa=0)
{
    siz[u]=1;
    for(const auto &e:G[u])
        if(e.v!=fa&&!disable[e.id])
        {
            E[e.v]=Edge(u,e.a,e.b,e.id);
            GetSize(e.v,u);
            siz[u]+=siz[e.v];
        }
}
int FindCentroid(int u,int lim,int fa=0)
{
    if(siz[u]<=lim)
        return u;
    int mxsiz=0,id;
    for(const auto &e:G[u])
        if(e.v!=fa&&!disable[e.id])
        {
            int tmp=FindCentroid(e.v,lim,u);
            if(siz[tmp]>mxsiz)
                mxsiz=siz[tmp],id=tmp;
        }
    return id;
}

void GetPath(int u,vector<Path> &P,Path now=Path(0,0),int fa=0)
{
    if(G[u].size()==1)
        P.push_back(now);
    for(const auto &e:G[u])
        if(e.v!=fa&&!disable[e.id])
            GetPath(e.v,P,Path(now.a+e.a,now.b+e.b),u);
}

void Process(vector<Path> &P)
{
    static vector<Path> tmp;
    sort(P.begin(),P.end());
    tmp.resize(P.size());
    tmp.emplace_back(0,0);
    int top=0;
    for(const auto &p:P)
    {
        while(top>0&&(p.a==tmp[top].a&&p.b>=tmp[top].b))
              top--;
        if(p.a==tmp[top].a&&p.b<=tmp[top].b)
            continue;
        while(top>0&&1.0*(tmp[top].b-tmp[top-1].b)/(tmp[top].a-tmp[top-1].a)<1.0*(p.b-tmp[top].b)/(p.a-tmp[top].a))
            top--;
        tmp[++top]=p;
    }
    for(int i=0; i<=top; i++)
        P[i]=tmp[i];
    P.resize(top+1);
}

vector<Path> P1,P2,P;

void CentroidDecomposition(int u)
{
    GetSize(u);
    if(siz[u]<=1)
        return;
    int centroid1=FindCentroid(u,siz[u]/2);
    int centroid2=E[centroid1].v;

    disable[E[centroid1].id]=true;
    P1.clear();
    P2.clear();
    P1.emplace_back(0,0);
    P2.emplace_back(0,0);
    GetPath(centroid1,P1);
    GetPath(centroid2,P2);

    Process(P1);
    Process(P2);

    int x=0,y=0;
    while(x<(int)P1.size()&&y<(int)P2.size())
    {
        P.emplace_back(P1[x].a+P2[y].a+E[centroid1].a,P1[x].b+P2[y].b+E[centroid1].b);
        double k1=-1e100,k2=-1e100;
        if(x<(int)P1.size()-1)
            k1=1.0*(P1[x+1].b-P1[x].b)/(P1[x+1].a-P1[x].a);
        if(y<(int)P2.size()-1)
            k2=1.0*(P2[y+1].b-P2[y].b)/(P2[y+1].a-P2[y].a);
        if(k1>k2)
            x++;
        else
            y++;
    }

    CentroidDecomposition(centroid1);
    CentroidDecomposition(centroid2);
}

int main()
{
    scanf("%d%d",&N,&M);
    F.n=N;
    for(int i=1; i<N; i++)
    {
        int u,v,a,b;
        scanf("%d%d%d%d",&u,&v,&a,&b);
        F.AddEdge(u,v,a,b,i);
    }

    G.n=N;
    ToBinaryTree(1);

    P.emplace_back(0,0);
    CentroidDecomposition(1);
    Process(P);

    int id=0;
    for(int t=0; t<M; t++)
    {
        while(id<(int)P.size()-1&&(1LL*t*P[id+1].a+P[id+1].b)>(1LL*t*P[id].a+P[id].b))
            id++;
        long long ans=1LL*t*P[id].a+P[id].b;
        printf("%I64d ",ans);
    }
    puts("");

    return 0;
}

题目大意 有一个A×B×C的长方体，将其分为a×b×c的小长方体若干块，且a≤b≤c，这样的(a,b,c)有多少组？

题解 及找有多少组(a,b,c)，使得这三个数中，一个为A的因数，另外有一个为B的因数，还有一个为C的因数。

如果直接用推组合数公式，就很容易陷入容斥的恐怖细节WA 黑 洞之中。

考虑把所有因数分组，使得每一组的因数都不同，将其分为7组，用二进制状态s表示： 第1位为1表示这个因数为A的因数 第2位为1表示这个因数为B的因数 第3位为1表示这个因数为C的因数 如101表示这个数为A与C的公因数，但不是B的因数

用cnt[s]表示状态为s的因数的个数（求cnt可用暴力卡过，但也有更好的办法，可见代码） 枚举a,b,c的状态（可相同），然后用组合数求出每种情况，然后加起来就是答案 如a,b都为状态s1，c为状态s2，则需要从cnt[s1]中选2个，cnt[s2]中选1个，即C(cnt[s1]+2−1,2)×C(cnt[s2]+1−1,1) （枚举状态时要判断状态是否合法：这三个状态是否包含ABC的因数）

Translated by Baidu:

Subject matter

There is a cuboid of A * B * C, which is divided into small cuboid blocks of a * b * C, and a is less than B = C, so how many (a, B, and C) are there?

An explanation

And how many groups (a, B, c) are found, so that one of these three numbers is the factor of A, another factor is B, and another factor is C.

If we use the combination formula directly, we can easily fall into the WA black hole which is contained in the horror details.

Considering that all factors are grouped so that the factors of each group are different, they are divided into 7 groups: binary s.

The factor of first is 1 that represents the factor of A

The factor of second is 1 that represents the factor of B

The factor of third is 1 that represents the factor of C

If 101 indicates that this number is a common factor of A and C, it is not a factor of B.

Using cnt[s] to represent the number of factors that state is s (CNT can be used by violent cards, but there is a better way to see the code).

Enumerate the state of a, B, C (the same), then use the combinatorial number to find out each case, and then add up the answer.

For example, a and B are state S1 and C are state S2, then we need to select 2 from cnt[s1] and 1 from cnt[s2], that is C (cnt[s1]+2 1,2) x (C).

(enumerating the state to determine whether the state is legal: does the three states contain the factor of ABC?)

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN=100005;

long long C(int n,int m)
{
    long long ret=1;
    for(int i=1;i<=m;i++)
        ret*=(n-i+1);
    for(int i=1;i<=m;i++)
        ret/=i;
    return ret;
}
bool check(int a,int b,int c)
{
    if((a&1)&&(b&2)&&(c&4))
        return true;
    if((a&1)&&(c&2)&&(b&4))
        return true;
    if((b&1)&&(a&2)&&(c&4))
        return true;
    if((b&1)&&(c&2)&&(a&4))
        return true;
    if((c&1)&&(a&2)&&(b&4))
        return true;
    if((c&1)&&(b&2)&&(a&4))
        return true;
    return false;
}
int gcd(int a,int b)
{
    if(b==0)
        return a;
    return gcd(b,a%b);
}

int n;
int q[MAXN],m;
int cnt[10],use[10];
int fac[MAXN];

int main()
{
//预处理因数个数
    for(int i=1;i<MAXN;i++)
        for(int j=i;j<MAXN;j+=i)
            fac[j]++;
    int T,X,Y,Z;
    scanf("%d",&T);
    long long ans;
    while(T--)
    {
        scanf("%d%d%d",&X,&Y,&Z);
        m=0;
        int xy=gcd(X,Y),yz=gcd(Y,Z),xz=gcd(X,Z);
        int xyz=gcd(xy,Z);
        //计算每种状态的因数个数
        cnt[7]=fac[xyz];//111
        cnt[6]=fac[yz]-fac[xyz];//110
        cnt[5]=fac[xz]-fac[xyz];//101
        cnt[4]=fac[Z]-fac[xz]-fac[yz]+fac[xyz];//100
        cnt[3]=fac[xy]-fac[xyz];//011
        cnt[2]=fac[Y]-fac[yz]-fac[xy]+fac[xyz];//010
        cnt[1]=fac[X]-fac[xy]-fac[xz]+fac[xyz];//001

        ans=0;
        for(int a=1;a<8;a++)
            for(int b=a;b<8;b++)
                for(int c=b;c<8;c++)
                    if(check(a,b,c))//检查合法
                    {
                        memset(use,0,sizeof use);
                        use[a]++;use[b]++;use[c]++;
                        long long tmp=1;
                        for(int i=1;i<8;i++)
                            if(use[i])
                                tmp*=C(cnt[i]+use[i]-1,use[i]);//组合数计算
                        if(tmp>0)
                            ans+=tmp;
                    }

        printf("%I64d\n",ans);
    }

    return 0;
}